湘教版备考2021年中考数学三轮复习专题10四边形
试卷更新日期：2021-05-17 类型：三轮冲刺
一、单选题
-
1. 如图，矩形 的四个顶点分别在矩形 的各条边上， ， ， ．有以下四个结论：① ；② ；③ ；④矩形 的面积是 ．其中正确的结论为（ ）
A、①② B、①②③ C、①②④ D、①②③④2. 如图，两个正方形边长分别为 、 ，如果 ， ，则图中阴影部分的面积为（ ）
A、144 B、72 C、68 D、363. 如图，在菱形ABCD中，∠A=60°，AD=8，F是AB的中点．过点F作FE⊥AD，垂足为E．将△AEF沿点A到点B的方向平移，得到△A'E'F'．设 P、P'分别是 EF、E'F'的中点，当点A'与点B重合时，四边形PP'CD的面积为（ ）
A、 B、 C、 D、 ﹣84. 如图四边形ABCD ， AD∥BC ， AB⊥BC ， AD=1，AB=2，BC=3，P为AB边上的一动点，以PD ， PC为边作平行四边形PCQD ， 则对角线PQ的长的最小值是（ ）
A、3 B、4 C、5 D、65. 如图，正方形ABCD中，点E、F、H分别是AB、BC、CD的中点，CE、DF交于G，连接AG、HG．下列结论：①CE⊥DF；②AG＝AD；③∠CHG＝∠DAG；④HG＝ AD．其中正确的有（ ）
A、1个 B、2个 C、3个 D、4个6. 如图，将矩形ABCD沿对角线AC剪开，再把△ACD沿CA方向平移得到△A1C1D1 ， 连结AD1 ， BC1 ． 若∠ACB＝30°，AB＝1，CC1＝x，△ACD与△A1C1D1重叠部分的面积为s，则下列结论：①△A1AD1≌△CC1B；②当x＝1时，四边形ABC1D1是菱形；③当x＝2时，△BDD1为等边三角形；④s＝ （x﹣2）2（0＜x＜2）。其中正确的有（ ）
A、1 个 B、2 个 C、3 个 D、4 个7. 如图，点A，B在直线l上两点，以AB为边作菱形ABCD，M、N分别是BC和CD的中点，NP⊥AB于点P，连接MP，若∠D=140°，则∠MPB的度数为（ ）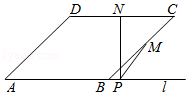
A、100° B、110° C、120° D、130°8. 在面积为12的平行四边形ABCD中，过点A作直线BC的垂线交直线BC于点E，过点A作直线CD的垂线交直线CD于点F，若AB=4，BC=6，则CE+CF的值为（ ）A、
B、
C、 或 
D、 或
9. 如图，矩形ABCD的面积为1cm2 ， 对角线交于点O；以AB、AO为邻边作平行四边形AOC1B，对角线交于点O1；以AB、AO1为邻边作平行四边形AO1C2B…；依此类推，则平行四边形AO2014C2015B的面积为（ ）
A、 B、 C、 D、10.如图，在四边形ABCD中，AB∥DC，AD=BC=5，DC=7，AB=13，点P从点A出发以3个单位/s的速度沿AD→DC向终点C运动，同时点Q从点B出发，以1个单位/s的速度沿BA向终点A运动．当四边形PQBC为平行四边形时，运动时间为（ ）
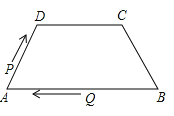A、4s B、3s C、2s D、1s11. 在下列条件中，不能确定四边形ABCD为平行四边形的是（ ）A、∠A=∠C，∠B=∠D B、∠A=∠B=∠C=90° C、∠A+∠B=180°，∠B+∠C=180° D、∠A+∠B=180°，∠C+∠D=180°12.如图，已知△ABC，分别以A，C为圆心，BC，AB长为半径画弧，两弧在直线BC上方交于点D，连接AD，CD，则有（ ）
A、∠ADC与∠BAD相等 B、∠ADC与∠BAD互补 C、∠ADC与∠ABC互补 D、∠ADC与∠ABC互余13.如图：在4×4的正方形（每个小正方形的边长均为1）网格中，以A为顶点，其他三个顶点都在格点（网格的交点）上，且面积为2的平行四边形的共有（ ）个．
A、10 B、12 C、14 D、23二、填空题
-
14. 如图是以正八边形为“基本单位”铺成的图案的一部分，（其中有4×3个“基本单位”），其间存有若干个小正方形空隙，以及图案的4个角处有更小的三角形空隙，若密铺5×4个“基本单位”的图案，并填满空隙，则需要个小正方形，小三角形．（不含图案的4个角）
15. 如图，在边长为1的菱形 ABCD中，∠ABC＝120°.连接对角线AC，以AC为边作第二个菱形ACEF，使∠ACE＝120°.连接AE，再以AE为边作第三个菱形AEGH，使 ∠AEG＝120°，…，按此规律所作的第n个菱形的边长是 ．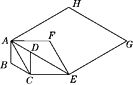
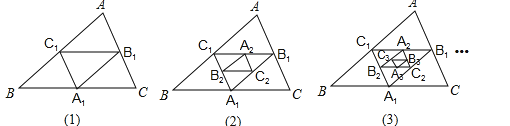
16. 凸n边形的对角线的条数记作an(n≥4)，例如：a4=2，那么：①a5=；②a6-a5=；③an+1-an=(n≥4，用含n的代数式表示).17. 对正方形剪一刀能得到边形．18.如图，在图（1）中，A1、B1、C1分别是△ABC的边BC、CA、AB的中点，在图（2）中，A2、B2、C2分别是△A1B1C1的边B1C1、C1A1、A1B1的中点，…，按此规律，则第n个图形中平行四边形的个数共有个
19.如图，△ABC中，AD是中线，AE是角平分线，CF⊥AE于F ， AB=5，AC=2，则DF的长为.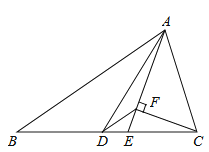
三、解答题
-
20. 如图，△ABC中，∠ACB=90°，D为AB中点，四边形BCED为平行四边形．DE、AC相交于点F．
(1)、求证：点F为AC中点；(2)、试确定四边形ADCE的形状，并说明理由；(3)、若四边形ADCE为正方形，△ABC应添加什么条件，并证明你的结论．21. 求证：三角形的外角和等于360° ． 一般地，n边形的外角和等于360°22. 如图：在△ABC中，∠BAC = ，AD⊥BC于D，CE平分∠ACB，交AD于G，交AB于E，EF⊥BC于F，求证：四边形AEFG是菱形.
23.在梯形ABCD中，AD∥BC ， AB=CD ， ∠AOD=60°，E为OA的中点，F为OB的中点，G为CD的中点，试判断△EFG的形状并说明理由 ．
四、作图题
-
24.
(1)、如图是一个多边形，你能否用一直线去截这个多边形，使得到的新多边形分别满足下列条件：（画出图形，把截去的部分打上阴影）
①新多边形内角和比原多边形的内角和增加了180°．
②新多边形的内角和与原多边形的内角和相等．
③新多边形的内角和比原多边形的内角和减少了180°．
(2)、将多边形只截去一个角，截后形成的多边形的内角和为2520°，求原多边形的边数．五、综合题
-
25. 如图①，在Rt△ABC中，∠ACB＝90°，∠A＜∠ABC，点D是边AB上的一个动点，过点D作DE⊥AC于点E，点F是射线ED上的点，DF=CB，连接BF、CD，得到四边形BCDF．
(1)、求证：四边形BCDF是平行四边形；(2)、若AB=8，∠A=30°，设AD= ，四边形BCDF的面积为 ．①求 关于 的函数表达式，并写出自变量 的取值范围；
②试问是否存在这样的点D使四边形BCDF为菱形? 若存在， 请求出 的值； 若不存在， 请说明理由．
26.问题探究：
【1】新知学习
⑴梯形的中位线：连接梯形两腰中点的线段叫做梯形的中位线．
⑵梯形的中位线性质：梯形的中位线平行于两底，并且等于两底和的一半．
⑶形如分式 （m为常数，且m＞0），若x＞0，则 ，并且有下列结论：
当x 逐渐增大时，分母x+2m逐渐增大，分式 的值逐渐减少并趋于0，但仍大于0．当x 逐渐减少时，分母x+2m逐渐减少，分式 的值逐渐增大并趋于 ，即趋于 ，但仍小于 ．
【2】问题解决
如图2，已知在梯形ABCD中，AD∥BC，AD＜BC，E、F分别是AB、CD的中点．
(1)、设AD=7，BC=17，求 的值．(2)、设AD=a（a为正的常数），BC=x，请问：当BC的长不断增大时， 的值能否大于或等于3，试证明你的结论．(3)、进一步猜想：任何一个梯形的中位线所分成的两部分图形的面积的比值所在的范围是什么，并说明理由．
27. 如图所示，在梯形ABCD中，AD∥BC，∠B=90°，AD=24cm，BC=26cm，动点P从点A出发沿AD方向向点D以1cm/s的速度运动，动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动．点P、Q分别从点A和点C同时出发，当其中一点到达端点时，另一点随之停止运动．
(1)、经过多长时间，四边形PQCD是平行四边形？(2)、经过多长时间，四边形PQBA是矩形？(3)、经过多长时间，当PQ不平行于CD时，有PQ=CD．28.如图，点P是∠AOB内的一点，过点P作PC∥OB，PD∥OA，分别交OA、OB于点C、D，且PE⊥OA，PF⊥OB，垂足分别为点E、F．
(1)、求证：OC•CE=OD•DF；
(2)、当点P位于∠AOB的什么位置时，四边形CODP是菱形并证明你的结论．
-