湘教版备考2021年中考数学三轮复习专题2方程与方程组（2）

试卷更新日期：2021-05-17 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 如图，表中给出的是2021年1月份的月历，任意选取“工”型框中的7个数（如阴影部分所示）．请你运用所学的数学知识来研究，则这7个数的和不可能是（）

A、76 B、91 C、140 D、16l

查看试题解析
2. 在长方形 $A B C D$ 中，放入6个形状大小完全相同的小长方形，所标尺寸如图所示，则小长方形的宽 $A E$ 的长度为（） cm .

A、1 B、1.6 C、2 D、2.5

查看试题解析
3. 甲车与乙车同时从A地出发去往B地，如图所示，折线O-A-B-C和射线OC分别是甲、乙两车行进过程中路程与时间的关系，已知甲车中途有事停留36分钟后再继续前往C地，两车同时到达C地，则下列说法：①乙车的速度为70千米/时；②甲车再次出发后的速度为100千米/时；③两车在到达B地前不会相遇；④甲车再次出发时，两车相距60千米。其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 郑奶奶提着篮子去农贸市场买鸡蛋，摊主按郑奶奶的要求，用电子秤称了5千克鸡蛋，郑奶奶怀疑重量不对，把鸡蛋放入自带的质量为0.6千克的篮子中(篮子质量准确)，要求放在电子秤上再称一遍，称得为5.75千克，老板客气地说：“除去篮子后为5.15千克，老顾客啦，多0.15千克就算了”，郑奶奶高兴地付了钱，满意地回家了．以下说法正确的是（）

A、郑奶奶赚了，鸡蛋的实际质量为5.15千克 B、郑奶奶亏了，鸡蛋的实际质量为4千克 C、郑奶奶亏了，鸡蛋的实际质量为4.85千克 D、郑奶奶不亏也不赚，鸡蛋的实际质量为5千克

查看试题解析
5. 医疗保险，住院治疗的病人享受分段报销，保险公司制定的报销细则如下表．某人住院治疗后得到保险公司报销金额是1100元，那么此人住院的医疗费是（）
住院医疗费（元）
报销率（%）
不超过500元的部分
0
超过500～1000元的部分
60
超过1000～3000元的部分
80
……

A、1000元 B、1250元 C、1500元 D、2000元

查看试题解析
6. 妈妈用2万元为小明存了一个6年期的教育储蓄，6年后，共能得23456元，则这种教育储蓄的年利率为（）

A、2.86% B、2.88% C、2.84% D、2.82%

查看试题解析
7. 若方程组 ${\begin{cases} a_{1} x + y = c_{1} \\ a_{2} x + y = c_{2} \end{cases}$ 的解是 ${\begin{cases} x = 2 \\ y = 3 \end{cases}$ ，则方程组 ${\begin{cases} a_{1} x + y = a_{1} - c_{1} \\ a_{2} x + y = a_{2} - c_{2} \end{cases}$ 的解是（）

A、 ${\begin{cases} x = 1 \\ y = 3 \end{cases}$ B、 ${\begin{cases} x = 1 \\ y = - 3 \end{cases}$ C、 ${\begin{cases} x = - 1 \\ y = 3 \end{cases}$ D、 ${\begin{cases} x = - 1 \\ y = - 3 \end{cases}$

查看试题解析
8. 利用两块相同的长方体木块测量一张桌子的高度．首先按图①方式放置，再交换两木块的位置，按图②方式放置．测量的数据如图，则桌子的高度是（）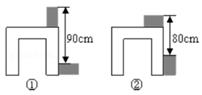

A、84cm B、85cm C、86cm D、87cm

查看试题解析

二、填空题

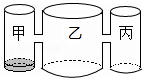
9. 实验室里，水平桌面上有甲、乙、丙三个圆柱形容器（容器足够高），底面半径之比为1：2：1，用两个相同的管子在容器的5cm高度处连通（即管子底端离容器底5cm）．现三个容器中，只有甲中有水，水位高1cm，如图所示．若每分钟同时向乙和丙注入相同量的水，开始注水1分钟，乙的水位上升 $\frac{5}{6}$ cm，则开始注入分钟的水量后，甲与乙的水位高度之差是0.5cm．

查看试题解析
10. 规定一种运算“*”，a*b= $\frac{1}{3}$ a﹣ $\frac{1}{4}$ b，则方程x*2=1*x的解为．

查看试题解析
11. 某商场经销一种商品，由于进货时价格比原进价降低了6.4%，使得利润率增加了8个百分点，那么经销这种商品原来的利润率是= $\frac{销售价 - 进价}{进价}$ ×100%）．

查看试题解析
12. 饮料由果汁、疏菜汁和纯净水按一定质量比配制而成，纯净水、果汁、蔬菜汁的价格比为1：2：2，因市场原因，果汁、蔬菜汁的价格涨了15%，而纯净水的价格降了20%，但并没有影响该饮料的成本（只考虑购买费用），那么该种饮料中果汁与蔬菜汁的质量和与纯净水的质量之比为．

查看试题解析
13. 甲、乙两人玩摸球游戏，从放有足够多球的箱子中摸球，规定每人最多两种取法，甲每次摸4个或（3－k）个，乙每次摸5个或（5－k）个(k是常数，且0＜k＜3)；经统计，甲共摸了16次，乙共摸了17次，并且乙至少摸了两次5个球，最终两人所摸出的球的总个数恰好相等，那么箱子中至少有球个

查看试题解析
14. 山脚下有一池塘，泉水以固定的流量（即单位时间里流入池中的水量相同）不停地向池塘内流淌．现池塘中有一定深度的水，若用一台A型抽水机抽水，则1小时正好能把池塘中的水抽完；若用两台A型抽水机抽水，则20分钟正好把池塘中的水抽完．问若用三台A型抽水机同时抽，则需要分钟恰好把池塘中的水抽完．

查看试题解析

三、计算题

15. 解关于x的方程 $\frac{x - a}{b} - \frac{x - b}{a} = \frac{b}{a}$ 其中 $a \neq 0 ， b \neq 0 ， a \neq b$

查看试题解析
16. 解关于x的方程 $4 m^{2} - x = 2 m x + 1$

查看试题解析
17. 已知：不论k取什么实数，关于x的方程 $\frac{2 k x + a}{3} - \frac{x - b k}{6} = 1$ （a、b是常数）的根总是x＝1，试求a、b的值。

查看试题解析
18. 判断下列二元一次方程有无整数解，并说明理由．

(1)、2x+6y=5；

(2)、4x+6y=8；

(3)、3x+5=6y+11；

(4)、 $x = \frac{11 - 2 y}{3}$ ．

查看试题解析
19. 求下列二元一次方程的解．

(1)、2x+6y=7；

(2)、-3x-3=4y+6．

查看试题解析

四、解答题

20. 某服装商场购进一批T恤，每件进价40元，出于营销考虑，要求每件售价不得低于40元且不得高于60元，在销售过程中发现该T恤每周的销售量 $y$ （件）与每件售价 $x$ （元）之间满足一次函数关系：当销售单价为44元时，销量是72件，当销售单价为48元时，销售量为64件.

(1)、请直接写出 $y$ 与 $x$ 的函数关系式；

(2)、当商场每周销售这种T恤获得350元的利润时，每件的销售单价是多少元？

(3)、设该商场每周销售这种T恤所获得的利润为 $w$ 元，将该T恤销售单价定为多少元时，才能使商场销售该T恤所获利润最大？最大利润是多少？

查看试题解析
21. 试将100分成两个正整数之和，其中一个为11的倍数，另一个为17的倍数．

查看试题解析
22. 已知a、b为正整数，并且 $\frac{2}{3}$ 、 $\frac{a}{4}$ 、 $\frac{b}{6}$ 都是既约真分数．如果 $\frac{2}{3}$ 、 $\frac{a}{4}$ 、 $\frac{b}{6}$ 的分子都加上b，得到的三个分数的和为6．求这三个既约真分数的积．

查看试题解析
23. 甲、乙两地相距60千米．一艘轮船往返于甲、乙两地之间，顺流时用4小时，逆流时用5小时．求这艘船在静水中的速度和流水的速度．

查看试题解析
24. 甲、乙两小组人数的和是28．如果甲组增加2人，乙组增加6人，那么甲组人数与乙组人数的比是2：1．求原来甲、乙两组的人数．

查看试题解析
25. 一个两位数，如果除以个位数字，得商为9余数为6；如果除以十位数字，得商为11余数为1．求这个两位数．

查看试题解析

五、综合题

26. 阅读理解：把几个数用大括号括起来，中间用逗号断开，比如： ${3, 2}$ ， ${- 2, 0 ， - 1}$ ，我们称之为集合，其中大括号内的数称为该集合的元素．如果一个集合满足：只要其中有一个元素 $a$ ，使得 $- 2 a + 3$ 也是这个集合的元素，我们把这样的集合称为自闭集合．例如：集合 ${- 2, 9, 7}$ ，因为 $- 2 \times (- 2) + 3 = 7$ ， $7$ 恰好是这个集合的元素，所以 ${- 2, 9, 7}$ 是自闭集合．再如：集合 ${- 1, 3}$ ，因为 $- 2 \times (- 1) + 3 = 5$ ，而 $5$ 不是这个集合的元素，且 $- 2 \times 3 + 3 = - 3$ ，而 $- 3$ 也不是这个集合的元素，所以 ${- 1, 3}$ 不是自闭集合

(1)、判断：集合 ${2, 4 ， - \frac{1}{2}}$ 自闭集合；（选填“是”或“不是”）

(2)、若集合 ${3, x}$ 和集合 ${- y}$ 都是自闭集合，求 $x + y$ 的值

查看试题解析
27. 如图所示，要在某东西走向的A、B两地之间修一条笔直的公路，在公路起点A处测得某农户C在A的北偏东68°方向上．在公路终点B处测得该农户C在点B的北偏西45°方向上．已知A、B两地相距2400米．

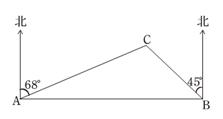(1)、求农户C到公路 $A B$ 的距离；（参考数据：sin22°≈ $\frac{3}{8}$ ，cos22°≈ $\frac{15}{16}$ ，tan22°≈ $\frac{2}{5}$ ）

(2)、现在由于任务紧急，要使该修路工程比原计划提前4天完成，需将该工程原定的工作效率提高20%，求原计划该工程队毎天修路多少米？

查看试题解析

28. 甲，乙两人沿湖边环形道上匀速跑步，他们开启了微信运动﹣﹣微信上实时统计每天步数的软件.已知乙的步距比甲的步距少0.4m(步距是指每一步的距离)，且每2分钟甲比乙多跑25步，两人各跑3周后到达同一地点，跑3圈前后的时刻和步数如下：

	出发时刻	出发时微信运动中显示的步数	结束时刻	结束时微信运动中显示的步数
甲	9：30	2158	9：40	4158
乙	a	1308	9：40	4308

(1)、求甲，乙的步距和环形道的周长；

(2)、求表中a的值；

(3)、若两人于9：40开始反向跑，问：此后，当微运动中显示的步数相差50步时，他们相遇了几次？

查看试题解析

29. 某商场计划经销A、B两种新型节能台灯共50盏，这两种台灯的进价、售价如下表所示．

A型
B型
进价（元/盏）
40
65
售价（元/盏）
60
100

(1)、若该商场购进这批台灯共用去2500元，问这两种台灯各购进多少盏？

(2)、在每种台灯销售利润不变的情况下，若该商场销售这批台灯的总利润不少于1400元，问至少需购进B种台灯多少盏？

(3)、若该商场预计用不少于2500元且不多于2600元的资金购进这批台灯，为了打开B种台灯的销路，商场决定每售出一盏B种台灯，返还顾客现金a元（10＜a＜20），问该商场该如何进货，才能获得最大的利润？

查看试题解析
30. 某汽车制造厂开发一款新式电动汽车，计划一年生产安装240辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装，工厂决定招聘一些新工人.他们经过培训后上岗，也能独立进行电动汽车的安装.生产开始后，调研部门发现：1名熟练工和2名新工人每月可安装8辆电动汽车；2名熟练工和3名新工人每月可安装14辆电动汽车.

(1)、每名熟练工和新工人每月分别可以安装多少辆电动汽车？

(2)、如果工厂招聘n（0<n<10）名新工人，使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务，那么工厂有哪几种新工人的招聘方案？

(3)、在（2）的条件下，工厂给安装电动汽车的每名熟练工每月发2000元的工资，给每名新工人每月发1200元的工资，那么工厂应招聘多少名新工人，使新工人的数量多于熟练工，同时工厂每月支出的工资总额W（元）尽可能的少？

查看试题解析

住院医疗费（元）	报销率（%）
不超过500元的部分	0
超过500～1000元的部分	60
超过1000～3000元的部分	80
……

	A型	B型
进价（元/盏）	40	65
售价（元/盏）	60	100