湘教版备考2021年中考数学三轮复习专题9三角形
试卷更新日期:2021-05-16 类型:三轮冲刺
一、单选题
-
1. 在等边三角形ABC所在的平面内存在点P,使⊿PAB、⊿PBC、⊿PAC都是等腰三角形.请指出具有这种性质的点P的个数( )
A、1 B、7 C、10 D、152. 如图,下列四个条件: ①BC=B′C;②AC=A′C;③∠A′CA=∠B′CB;④AB=A′B′.从中任取三个为条件,余下的一个为结论,则最多可以构成正确的结论的个数是( ) A、1 B、2 C、3 D、43. 如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )
A、1 B、2 C、3 D、43. 如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC,∠CED=35°,则∠EAB的度数是( )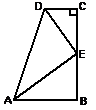 A、65° B、55° C、45° D、35°4. 如图,在 格的正方形网格中,与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点在格点上的三角形)共有( )
A、65° B、55° C、45° D、35°4. 如图,在 格的正方形网格中,与△ABC有一条公共边且全等(不与△ABC重合)的格点三角形(顶点在格点上的三角形)共有( ) A、5个 B、6 个 C、7个 D、8 个5. 如图,在△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长为( )
A、5个 B、6 个 C、7个 D、8 个5. 如图,在△ABC中,∠ABC=45°,F是高AD和BE的交点,CD=4,则线段DF的长为( ) A、3 B、4 C、5 D、66. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等.
A、3 B、4 C、5 D、66. 已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=2,连接DE,动点P从点B出发,以每秒2个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为( )秒时,△ABP和△DCE全等. A、1 B、1或3 C、1或7 D、3或77. 如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2 , 依此类推,∠A4BC与∠A4CD的平分线相交于点A5 , 则∠A5的度数为( )
A、1 B、1或3 C、1或7 D、3或77. 如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2 , 依此类推,∠A4BC与∠A4CD的平分线相交于点A5 , 则∠A5的度数为( ) A、19.2° B、8° C、6° D、3°8. 如图,已知AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4…,若∠A=70°,则∠An﹣1AnBn﹣1(n>2)的度数为( )
A、19.2° B、8° C、6° D、3°8. 如图,已知AB=A1B,A1B1=A1A2 , A2B2=A2A3 , A3B3=A3A4…,若∠A=70°,则∠An﹣1AnBn﹣1(n>2)的度数为( ) A、 B、 C、 D、9. 如图所示的正方形网格中,网格线的交点称为格点,已知A,B是两格点,若C也是格点,且使得△ABC为等腰三角形,则点C的个数是( )
A、 B、 C、 D、9. 如图所示的正方形网格中,网格线的交点称为格点,已知A,B是两格点,若C也是格点,且使得△ABC为等腰三角形,则点C的个数是( ) A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9二、填空题
-
10. 的最小值为。
11. 已知 中, , ,点 为 的中点,点 、 分别为边 、 上的动点,且 ,连接 ,下列说法正确的是.(写出所有正确结论的序号)① ;② ;③ ;④
 12. △ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC= .现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为 .
12. △ABC与△DEF是两个全等的等腰直角三角形,∠BAC=∠D=90°,AB=AC= .现将△DEF与△ABC按如图所示的方式叠放在一起,使△ABC保持不动,△DEF运动,且满足点E在边BC上运动(不与B,C重合),边DE始终经过点A,EF与AC交于点M.在△DEF运动过程中,若△AEM能构成等腰三角形,则BE的长为 .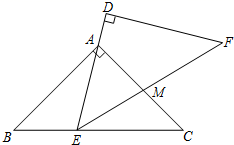 13. 如图,在 中, , 是 的中点, , , , 是垂足,现给出以下四个结论:① ;② ;③ 垂直平分 ;④ .其中正确结论的个数是 .
13. 如图,在 中, , 是 的中点, , , , 是垂足,现给出以下四个结论:① ;② ;③ 垂直平分 ;④ .其中正确结论的个数是 . 14. 如图, 是 的中线, 、 分别是 和 延长线上的点,且 ,连接 、 ,下列说法:① 和 的面积相等,② ,③ ,④ ,⑤ ,其中一定正确的答案有 . (只填写正确的序号)
14. 如图, 是 的中线, 、 分别是 和 延长线上的点,且 ,连接 、 ,下列说法:① 和 的面积相等,② ,③ ,④ ,⑤ ,其中一定正确的答案有 . (只填写正确的序号)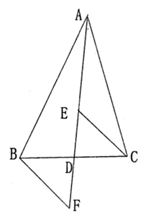 15. 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是 .
15. 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是 .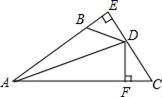 16. 如图,在四边形ABCD中,∠B=∠C=90°,∠DAB与∠ADC的平分线相交于BC边上的M点.有下列结论:①∠AMD=90°;②M为BC的中点;③AB+CD=AD;④S△ADM=S梯形ABCD;⑤M到AD的距离等于BC的一半.其中正确的结论有
16. 如图,在四边形ABCD中,∠B=∠C=90°,∠DAB与∠ADC的平分线相交于BC边上的M点.有下列结论:①∠AMD=90°;②M为BC的中点;③AB+CD=AD;④S△ADM=S梯形ABCD;⑤M到AD的距离等于BC的一半.其中正确的结论有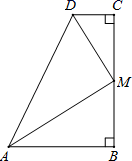 17. 我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内正六边形的面积S6 , 则S6= .18. 如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是(用含m的代数式表示)
17. 我国古代数学家刘徽创立的“割圆术”可以估算圆周率π,理论上能把π的值计算到任意精度.祖冲之继承并发展了“割圆术”,将π的值精确到小数点后七位,其结果领先世界一千多年.“割圆术”的第一步是计算单位圆内正六边形的面积S6 , 则S6= .18. 如图,在等腰Rt△ABC中,∠ABC=90°,AB=CB=2,点D为AC的中点,点E,F分别是线段AB,CB上的动点,且∠EDF=90°,若ED的长为m,则△BEF的周长是(用含m的代数式表示)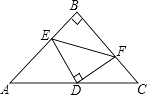
三、解答题
-
19.
如图1,把边长为4的正三角形各边四等分,连接各分点得到16个小正三角形.
 (1)、如图2,连接小正三角形的顶点得到的正六边形ABCDEF的周长=(2)、请你判断:命题“六个内角相等的六边形是正六边形”是真命题还是假命题如果是真命题,请你把它改写成“如果…,那么…”的形式;如果是假命题,请在图1中画图说明.20. 如图,四边形ABCD中,AC为∠BAD的角平分线,AB=AD,E、F两点分别在AB、AD上,且AE=DF.请完整说明为何四边形AECF的面积为四边形ABCD的一半.
(1)、如图2,连接小正三角形的顶点得到的正六边形ABCDEF的周长=(2)、请你判断:命题“六个内角相等的六边形是正六边形”是真命题还是假命题如果是真命题,请你把它改写成“如果…,那么…”的形式;如果是假命题,请在图1中画图说明.20. 如图,四边形ABCD中,AC为∠BAD的角平分线,AB=AD,E、F两点分别在AB、AD上,且AE=DF.请完整说明为何四边形AECF的面积为四边形ABCD的一半. 21. 阅读:能够成为直角三角形的三边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组的公式为 其中m>n>0,m,n是互质的奇数.
21. 阅读:能够成为直角三角形的三边长的三个正整数a,b,c,称为勾股数.世界上第一次给出勾股数通解公式的是我国古代数学著作《九章算术》,其勾股数组的公式为 其中m>n>0,m,n是互质的奇数.应用:当n=1时,求有一边长为5的直角三角形的另外两条边的长.
22. 如图,已知△ABC≌△ADE,AB与ED交于点M,BC与ED,AD分别交于点F,N.请写出图中两对全等三角形(△ABC≌△ADE除外),并选择其中的一对加以说明. 23. 如图①, cm, , , cm.点 在线段 上以1 cm/s的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动.它们运动的时间为 s.
23. 如图①, cm, , , cm.点 在线段 上以1 cm/s的速度由点 向点 运动,同时,点 在线段 上由点 向点 运动.它们运动的时间为 s.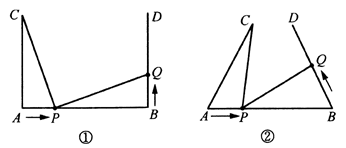 (1)、若点 的运动速度与点 的运动速度相等,当 时, 与 是否全等,请说明理由,并判断此时线段 和线段 的位置关系;(2)、如图②,将图①中的“ , ”改为“ ”,其他条件不变.设点 的运动速度为 cm/s,是否存在实数 ,使得 与 全等?若存在,求出相应的 的值;若不存在,请说明理由.24. 如图所示,在 △ ABC中, ∠ABC=∠C,BD⊥AC交AC于D.求证: ∠DBC= ∠A.
(1)、若点 的运动速度与点 的运动速度相等,当 时, 与 是否全等,请说明理由,并判断此时线段 和线段 的位置关系;(2)、如图②,将图①中的“ , ”改为“ ”,其他条件不变.设点 的运动速度为 cm/s,是否存在实数 ,使得 与 全等?若存在,求出相应的 的值;若不存在,请说明理由.24. 如图所示,在 △ ABC中, ∠ABC=∠C,BD⊥AC交AC于D.求证: ∠DBC= ∠A.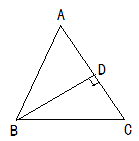 25. 如图, ∠A=80°, ∠ABC的平分线和 ∠ACB的外角平分线相交于D,求∠D的大小.
25. 如图, ∠A=80°, ∠ABC的平分线和 ∠ACB的外角平分线相交于D,求∠D的大小. 26. 如图,在 △ABC中,AD是∠BAC的平分线,BE⊥AD交AD的延长线于E,求证: ∠ABE<∠ACB.
26. 如图,在 △ABC中,AD是∠BAC的平分线,BE⊥AD交AD的延长线于E,求证: ∠ABE<∠ACB. 27. 如图,P为△ABC内的一点.求证: ∠BPC> ∠A
27. 如图,P为△ABC内的一点.求证: ∠BPC> ∠A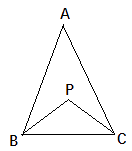
四、作图题
-
28. 仅用无刻度的直尺作出符合下列要求的图形.
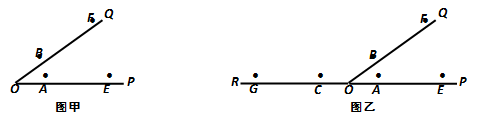 (1)、如图甲,在射线OP、OQ上已截取OA=OB,OE=OF.试过点O作射线OM,使得OM将∠POQ平分;(2)、如图乙,在射线OP、OQ、OR上已截取OA=OB=OC,OE=OF=OG(其中OP、OR在同一根直线上). 试过点O作一对射线OM、ON,使得OM⊥ON.29.
(1)、如图甲,在射线OP、OQ上已截取OA=OB,OE=OF.试过点O作射线OM,使得OM将∠POQ平分;(2)、如图乙,在射线OP、OQ、OR上已截取OA=OB=OC,OE=OF=OG(其中OP、OR在同一根直线上). 试过点O作一对射线OM、ON,使得OM⊥ON.29.已知:如图△ABC .
求作:①AC边上的高BD;
②△ABC的角平分线CE .

五、综合题
-
30. 如图,⊙O是△ABC的外接圆,弦BD交AC于点E,连接CD,且AE=DE,BC=CE.
 (1)、求∠ACB的度数;
(1)、求∠ACB的度数;
(2)、过点O作OF⊥AC于点F,延长FO交BE于点G,DE=3,EG=2,求AB的长.
31. (1)、如图①所示,P是等边△ABC内的一点,连接PA,PB,PC,将△BAP绕B点顺时针旋转60°。得△BCQ,连接PQ.若PA2+PB2=PC2 , 证明∠PQC=90°;
(1)、如图①所示,P是等边△ABC内的一点,连接PA,PB,PC,将△BAP绕B点顺时针旋转60°。得△BCQ,连接PQ.若PA2+PB2=PC2 , 证明∠PQC=90°;
(2)、如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA,PB,PC,将 △BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PQ,PB,PC满足什么条件时∠PQC=90°?请说明.32. 如图,在Rt ABC中,∠C=90°,AC=BC=4cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以 的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为他t(s).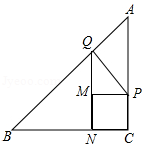 (1)、当t为何值时,点B在线段PQ的垂直平分线上?(2)、是否存在某一时刻t,使 APQ是以PQ为腰的等腰三角形?若存在,求出 的值;若不存在,请说明理由;(3)、以PC为边,往CB方向作正方形CPMN,设四边形QNCP的面积为S,求S关于t的函数关系式.33. 以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.
(1)、当t为何值时,点B在线段PQ的垂直平分线上?(2)、是否存在某一时刻t,使 APQ是以PQ为腰的等腰三角形?若存在,求出 的值;若不存在,请说明理由;(3)、以PC为边,往CB方向作正方形CPMN,设四边形QNCP的面积为S,求S关于t的函数关系式.33. 以点A为顶点作两个等腰直角三角形(△ABC,△ADE),如图1所示放置,使得一直角边重合,连接BD,CE.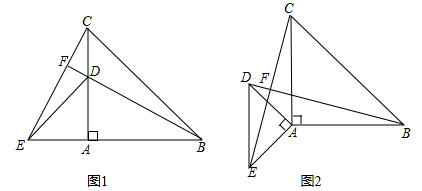 (1)、说明BD=CE;(2)、延长BD,交CE于点F,求∠BFC的度数;(3)、若如图2放置,上面的结论还成立吗?请简单说明理由.34. 如图,是一个4×4的方格,
(1)、说明BD=CE;(2)、延长BD,交CE于点F,求∠BFC的度数;(3)、若如图2放置,上面的结论还成立吗?请简单说明理由.34. 如图,是一个4×4的方格,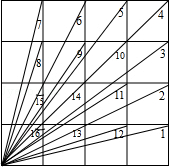 (1)、求图中∠1+∠2+∠3+∠4+…+∠16的和.(2)、求∠1﹣∠2+∠3﹣∠4+…+∠15﹣∠16.35.
(1)、求图中∠1+∠2+∠3+∠4+…+∠16的和.(2)、求∠1﹣∠2+∠3﹣∠4+…+∠15﹣∠16.35.
如图(1):已知在△ABC中,AB=AC,P是底边BC上一点,作PD⊥AB于D,PE⊥AC于E,BF⊥AC于F,求证:PD+PE=BF.
【思路梳理】:如图(2):连接AP,必有S△APB+S△APC=S△ABC , 因为△ABP、△ACP和△ABC的底相等,所以三条高PD、PE和BF满足关系:PD+PE=BF.
(1)、【变式应用】:如图(3):已知在△ABC中,AB=AC,P是底边BC的反向延长线上一点,作PD⊥AB于D,PE⊥AC于E,BF⊥AC于F,求证:PE﹣PD=BF.(2)、【类比引申】:如图(4):已知P是边长为4cm等边△ABC内部一点,作PD⊥BC于D,PE⊥AB于E,PF⊥AC于F,那么PD+PE+PF= .(3)、【联想拓展】:已知某三角形的三条边分别是5cm、12cm、13cm,在平面上有一点P,它到此三角形的三边的距离相等,则这个距离等于 .36.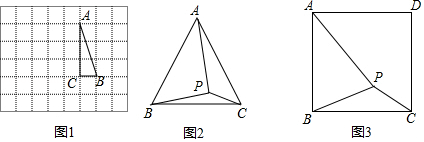 (1)、(操作发现)
(1)、(操作发现)如图1,在边长为1个单位长度的小正方形组成的网格中,△ABC的三个顶点均在格点上.请接要求画图:将△ABC绕点A按顺时针方向旋转90°,点B的对应点为B′,点C的对应点为C′,连接BB′,则∠AB′B= .
(2)、(问题解决)如图2,在等边三角形ABC内有一点P,且PA=2,PB= ,PC=1,求∠BPC的度数和等边三角形ABC的边长;
(3)、(灵活运用)如图3,在正方形ABCD内有一点P,且PA= ,BP= ,PC=1,求∠BPC的度数.
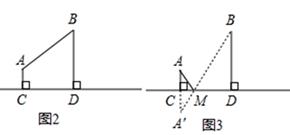
37. 如图,△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点A出发,以每秒1cm的速度沿折线A﹣C﹣B﹣A运动,设运动时间为t秒(t>0). (1)、当点P在AC上,且满足PA=PB时,求出此时t的值;(2)、当点P在AB上,求出t为何值时,△BCP为等腰三角形.38. 如图1中A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
(1)、当点P在AC上,且满足PA=PB时,求出此时t的值;(2)、当点P在AB上,求出t为何值时,△BCP为等腰三角形.38. 如图1中A村和B村在一条大河CD的同侧,它们到河岸的距离AC、BD分别为1千米和4千米,又知道CD的长为4千米.
 (1)、现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.
(1)、现要在河岸CD上建一水厂向两村输送自来水.有两种方案备选.方案1:水厂建在C点,修自来水管道到A村,再到B村(即AC+AB).(如图2)
方案2:作A点关于直线CD的对称点A′,连接A′B交CD于M点,水厂建在M点处,分别向两村修管道AM和BM.(即AM+BM)(如图3)
从节约建设资金方面考虑,将选择管道总长度较短的方案进行施工.请利用已有条件分别进行计算,判断哪种方案更合适.
(2)、有一艘快艇Q从这条河中驶过,当快艇Q与CD中点G相距多远时,△ABQ为等腰三角形?直接写出答案,不要说明理由.