湘教版备考2021年中考数学三轮复习专题8函数综合
试卷更新日期:2021-05-16 类型:三轮冲刺
一、单选题
-
1. 我们把1,1,2,3,5,8,13,21,…,这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧 , , ,…,得到斐波那契螺旋线,然后顺次连结P1P2 , P2P3 , P3P4 , …,得到螺旋折线(如图),已知点P1(0,1),P2(-1,0),P3(0,-1),则该折线上的点P9的坐标为( )
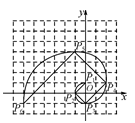 A、(-6,24) B、(-6,25) C、(-5,24) D、(-5,25)2. 一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:( )
A、(-6,24) B、(-6,25) C、(-5,24) D、(-5,25)2. 一个寻宝游戏的寻宝通道如图①所示,通道由在同一平面内的AB,BC,CA,OA, OB,OC组成。为记录寻宝者的行进路线,在BC的中点M处放置了一台定位仪器,设寻宝者行进的时间为x,寻宝者与定位仪器之间的距离为y,若寻宝者匀速行进,且表示y与x的函数关系的图像大致如图②所示,则寻宝者的行进路线可能为:( ) A、A→O→B B、B→A→C C、B→O→C D、C→B→O3. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )
A、A→O→B B、B→A→C C、B→O→C D、C→B→O3. 如图,边长分别为1和2的两个等边三角形,开始它们在左边重合,大三角形固定不动,然后把小三角形自左向右平移直至移出大三角形外停止.设小三角形移动的距离为x,两个三角形重叠面积为y,则y关于x的函数图象是( )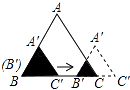 A、
A、 B、
B、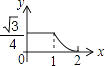 C、
C、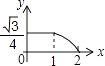 D、
D、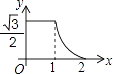 4. 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( )
4. 已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论正确的是( ) A、ac>0 B、当x>0时,y随x的增大而减小 C、2a﹣b=0 D、方程ax2+bx+c=0的两根是x1=﹣1,x2=35. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1、x2 , 其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a<﹣1;④b2+8a>4ac.其中正确的有( )
A、ac>0 B、当x>0时,y随x的增大而减小 C、2a﹣b=0 D、方程ax2+bx+c=0的两根是x1=﹣1,x2=35. 如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(﹣1,2),且与x轴交点的横坐标分别为x1、x2 , 其中﹣2<x1<﹣1,0<x2<1,下列结论:①4a﹣2b+c<0;②2a﹣b<0;③a<﹣1;④b2+8a>4ac.其中正确的有( )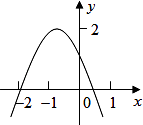 A、1个 B、2个 C、3个 D、4个6. 下列四个函数:①y=﹣ ;②y=2(x+1)2﹣3;③y=﹣2x+5;④y=3x﹣10.其中,当x>﹣1时,y随x的增大而增大的函数是( )A、①④ B、②③ C、②④ D、①②7. 设A(﹣2,y1),B(﹣1,y2),C(2,y3)是抛物线y=﹣2(x﹣1)2+k(k为常数)上的三点,则y1 , y2 , y3的大小关系为( )A、y3>y2>y1 B、y1>y2>y3 C、y3>y1>y2 D、y2>y3>y18. 给出下列命题及函数y=x与y=x2和 的图象:
A、1个 B、2个 C、3个 D、4个6. 下列四个函数:①y=﹣ ;②y=2(x+1)2﹣3;③y=﹣2x+5;④y=3x﹣10.其中,当x>﹣1时,y随x的增大而增大的函数是( )A、①④ B、②③ C、②④ D、①②7. 设A(﹣2,y1),B(﹣1,y2),C(2,y3)是抛物线y=﹣2(x﹣1)2+k(k为常数)上的三点,则y1 , y2 , y3的大小关系为( )A、y3>y2>y1 B、y1>y2>y3 C、y3>y1>y2 D、y2>y3>y18. 给出下列命题及函数y=x与y=x2和 的图象:①如果 >a>a2 , 那么0<a<1;
②如果a2>a> ,那么a>1或﹣1<a<0;
③如 >a2>a,那么﹣1<a<0;
④如果a2> >a,那么a<﹣1.则( )
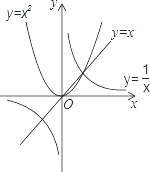 A、正确的命题只有① B、正确的命题有①②④ C、错误的命题有②③ D、错误的命题是③④9. 如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )
A、正确的命题只有① B、正确的命题有①②④ C、错误的命题有②③ D、错误的命题是③④9. 如图,点A1、A2、A3、…、An在抛物线y=x2图象上,点B1、B2、B3、…、Bn在y轴上,若△A1B0B1、△A2B1B2、…、△AnBn﹣1Bn都为等腰直角三角形(点B0是坐标原点),则△A2014B2013B2014的腰长等于( )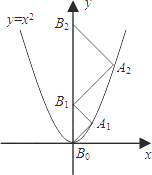 A、2013 B、2014 C、2013 D、201410. 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒 个单位长度,则第2015秒时,点P的坐标是( )
A、2013 B、2014 C、2013 D、201410. 如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3 , …组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒 个单位长度,则第2015秒时,点P的坐标是( )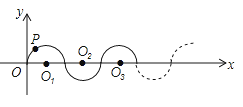 A、(2014,0) B、(2015,-1) C、(2015,1) D、(2016,0)11. 如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ,其中正确的个数有( )
A、(2014,0) B、(2015,-1) C、(2015,1) D、(2016,0)11. 如图,一次函数y=ax+b的图象与x轴、y轴交于A、B两点,与反比例函数 的图象相交于C、D两点,分别过C、D两点作y轴,x轴的垂线,垂足为E、F,连接CF、DE,有下列结论:①△CEF与△DEF的面积相等;②EF∥CD;③△DCE≌△CDF;④AC=BD;⑤△CEF的面积等于 ,其中正确的个数有( )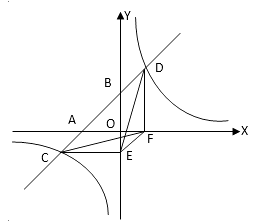 A、2 B、3 C、4 D、512. 如图,正方形ABCE的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,则△MAN的面积的最小值为( )
A、2 B、3 C、4 D、512. 如图,正方形ABCE的边长为1,点M、N分别在BC、CD上,且△CMN的周长为2,则△MAN的面积的最小值为( )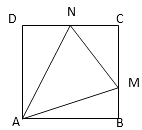 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 某服装店购进单价为15元童装若干件,销售一段时间后发现:当销售价为25元时平均每天能售出8件,而当销售价每降低2元,平均每天能多售出4件,当每件的定价为元时,该服装店平均每天的销售利润最大.14. 如图,已知点 、 在双曲线 上, 轴于点 , 轴于点 , 与 交于点 , 是 的中点,若 的面积为 ,则 的值等于 .
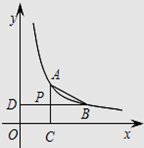 15. 如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0)、A(0,6)、B(4,6)、C(4,4)、D(6,4),E(6,0),若直线L经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线L的函数表达式是
15. 如图,在平面直角坐标系中,多边形OABCDE的顶点坐标分别是O(0,0)、A(0,6)、B(4,6)、C(4,4)、D(6,4),E(6,0),若直线L经过点M(2,3),且将多边形OABCDE分割成面积相等的两部分,则直线L的函数表达式是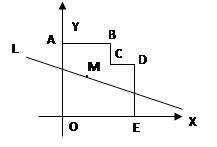 16. 数y=ax2+bx+c(a<0)图象与x轴的交点A.B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:
16. 数y=ax2+bx+c(a<0)图象与x轴的交点A.B的横坐标分别为﹣3,1,与y轴交于点C,下面四个结论:①16a﹣4b+c<0;②若P(﹣5,y1),Q( ,y2)是函数图象上的两点,则y1>y2;③a=﹣ c;④若△ABC是等腰三角形,则b=﹣ .其中正确的有(请将结论正确的序号全部填上)
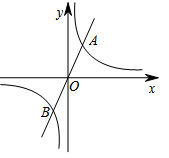
17. 如图,矩形 的对角线 经过的坐标原点,矩形的边分别平行于坐标轴,点 在反比例函数 的图象上,若点 的坐标为 ,则 的值为 . 18. 如图,直线 与双曲线 交于 、 两点,若 、 两点的坐标分别为 , ,则 的值为 .
18. 如图,直线 与双曲线 交于 、 两点,若 、 两点的坐标分别为 , ,则 的值为 .
 19. 已知抛物线y=x2﹣2x﹣3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=﹣x+n与此图象有且只有两个公共点时,则n的取值范围为 .
19. 已知抛物线y=x2﹣2x﹣3与x轴相交于A、B两点,其顶点为M,将此抛物线在x轴下方的部分沿x轴翻折,其余部分保持不变,得到一个新的图象.如图,当直线y=﹣x+n与此图象有且只有两个公共点时,则n的取值范围为 .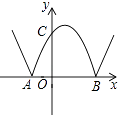
三、解答题
-
20. 如图1,已知二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为﹣ ,直线l的解析式为y=x.
 (1)、求二次函数的解析式;(2)、直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;(3)、在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.21. 如图双曲线 与矩形 AOCB 的边 AB 、 BC 分别交于 E 、 F 点, OA 、 OC 在坐标轴上,BE=2AE 且S四边形OEBF=2,求 k .
(1)、求二次函数的解析式;(2)、直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;(3)、在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.21. 如图双曲线 与矩形 AOCB 的边 AB 、 BC 分别交于 E 、 F 点, OA 、 OC 在坐标轴上,BE=2AE 且S四边形OEBF=2,求 k . 22. 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,8),点P在边BC上以每秒1个单位长的速度由点C向点B运动,同时点Q在边AB上以每秒a个单位长的速度由点A向点B运动,运动时间为t秒(t>0).
22. 如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,8),点P在边BC上以每秒1个单位长的速度由点C向点B运动,同时点Q在边AB上以每秒a个单位长的速度由点A向点B运动,运动时间为t秒(t>0).(1)若反比例函数y=图象经过P点、Q点,求a的值;
(2)若OQ垂直平分AP,求a的值;
(3)当Q点运动到AB中点时,是否存在a使△OPQ为直角三角形?若存在,求出a的值,若不存在请说明理由;
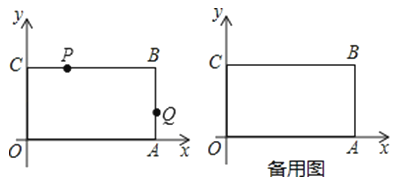 23. 小明在复习数学知识时,针对“求一元二次方程的解”整理了以下几种方法,请你将有关内容补充完整:
23. 小明在复习数学知识时,针对“求一元二次方程的解”整理了以下几种方法,请你将有关内容补充完整:例题:求一元二次方程x2﹣x﹣1=0的两个解.
(1)、解法一:(1)选择合适的一种方法(公式法、配方法、分解因式法).(2)、(2)解法二:利用二次函数图象与坐标轴的交点求解,如图(1)所示,①把方程x2-x-1=0的解看成是二次函数y= 的图象与x 轴交点的横坐标,即x1 , x2就是方程的解。②画出这两个函数的图象 ,用x1 , x2在x轴上标出方程的解。
四、作图题
-
24. 已知二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),C(0,3).
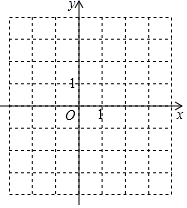 (1)、求二次函数的解析式;(2)、在图中,画出二次函数的图象;(3)、根据图象,直接写出当y≤0时,x的取值范围.25. 把y= x2的图象向上平移2个单位.(1)、求新图象的解析式、顶点坐标和对称轴;(2)、画出平移后的函数图象;(3)、求平移后的函数的最大值或最小值,并求对应的x的值.26. 已知反比例函数的图象过点 .
(1)、求二次函数的解析式;(2)、在图中,画出二次函数的图象;(3)、根据图象,直接写出当y≤0时,x的取值范围.25. 把y= x2的图象向上平移2个单位.(1)、求新图象的解析式、顶点坐标和对称轴;(2)、画出平移后的函数图象;(3)、求平移后的函数的最大值或最小值,并求对应的x的值.26. 已知反比例函数的图象过点 . (1)、这个反比例函数图象分布在哪些象限? 随 的增大而如何变化?(2)、点 , 和 哪些点在图象上?(3)、画出这个函数的图象.27. 已知函数y= 的图象经过点(-3,4).
(1)、这个反比例函数图象分布在哪些象限? 随 的增大而如何变化?(2)、点 , 和 哪些点在图象上?(3)、画出这个函数的图象.27. 已知函数y= 的图象经过点(-3,4).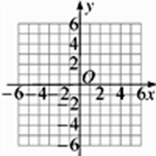 (1)、求k的值,并在正方形网格中画出这个函数的图象;(2)、当x取什么值时,函数的值小于0?
(1)、求k的值,并在正方形网格中画出这个函数的图象;(2)、当x取什么值时,函数的值小于0?五、综合题
-
28. 如图 ,抛物线 与 轴交于 ,与 轴交于点 .已知直线 过 两点.
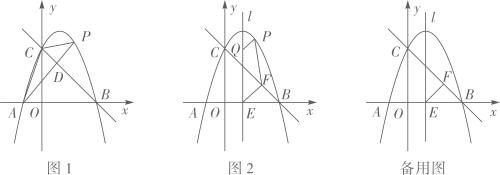 (1)、求抛物线和直线 的表达式;(2)、点 是抛物线上的一个动点,
(1)、求抛物线和直线 的表达式;(2)、点 是抛物线上的一个动点,①如图 ,若点 在第一象限内,连接 ,交直线 于点 .设 的面积为 , 的面积为 ,求 的最大值;
②如图2,抛物线的对称轴 与 轴交于点 ,过点 作 ,垂足为 .点 是对称轴 上的一个动点,是否存在以点 为顶点的四边形是平行四边形?
若存在,求出点 的坐标;若不存在,请说明理由.
29. 已知抛物线 (b , c为常数).(1)、若抛物线的顶点坐标为(1,1),求b , c的值;(2)、若抛物线上始终存在不重合的两点关于原点对称,求c的取值范围;(3)、在(1)的条件下,存在正实数m , n( m<n),当m≤x≤n时,恰好有 ,求m , n的值.30. 在平面直角坐标系xOy中,顶点为A的抛物线与x轴交于B、C两点,与y轴交于点D,已知A(1,4),B(3,0).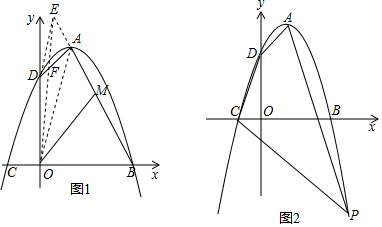 (1)、求抛物线对应的二次函数表达式;(2)、探究:如图1,连接OA,作DE∥OA交BA的延长线于点E,连接OE交AD于点F,M是BE的中点,则OM是否将四边形OBAD分成面积相等的两部分?请说明理由;(3)、应用:如图2,P(m,n)是抛物线在第四象限的图象上的点,且m+n=﹣1,连接PA、PC,在线段PC上确定一点M,使AN平分四边形ADCP的面积,求点N的坐标.提示:若点A、B的坐标分别为(x1 , y1)、(x2 , y2),则线段AB的中点坐标为( , ).31. 已知抛物线F:y=x2+bx+c的图象经过坐标原点O,且与x轴另一交点为( ,0).
(1)、求抛物线对应的二次函数表达式;(2)、探究:如图1,连接OA,作DE∥OA交BA的延长线于点E,连接OE交AD于点F,M是BE的中点,则OM是否将四边形OBAD分成面积相等的两部分?请说明理由;(3)、应用:如图2,P(m,n)是抛物线在第四象限的图象上的点,且m+n=﹣1,连接PA、PC,在线段PC上确定一点M,使AN平分四边形ADCP的面积,求点N的坐标.提示:若点A、B的坐标分别为(x1 , y1)、(x2 , y2),则线段AB的中点坐标为( , ).31. 已知抛物线F:y=x2+bx+c的图象经过坐标原点O,且与x轴另一交点为( ,0). (1)、求抛物线F的解析式;(2)、如图1,直线l:y x+m(m>0)与抛物线F相交于点A(x1 , y1)和点B(x2 , y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);(3)、在(2)中,若m ,设点A′是点A关于原点O的对称点,如图2.
(1)、求抛物线F的解析式;(2)、如图1,直线l:y x+m(m>0)与抛物线F相交于点A(x1 , y1)和点B(x2 , y2)(点A在第二象限),求y2﹣y1的值(用含m的式子表示);(3)、在(2)中,若m ,设点A′是点A关于原点O的对称点,如图2.①判断△AA′B的形状,并说明理由;
②平面内是否存在点P,使得以点A、B、A′、P为顶点的四边形是菱形?若存在,求出点P的坐标;若不存在,请说明理由.
32. 如图,抛物线y=ax2+bx+c(a、b、c为常数,a≠0)经过点A(﹣1,0),B(5,﹣6),C(6,0).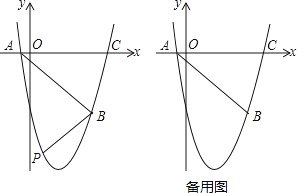 (1)、求抛物线的解析式;(2)、如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.
(1)、求抛物线的解析式;(2)、如图,在直线AB下方的抛物线上是否存在点P使四边形PACB的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;(3)、若点Q为抛物线的对称轴上的一个动点,试指出△QAB为等腰三角形的点Q一共有几个?并请求出其中某一个点Q的坐标.