浙教版备考2021年中考数学三轮冲刺复习专题16 尺规作图
试卷更新日期:2021-05-16 类型:三轮冲刺
一、单选题
-
1. 如图,依据尺规作图的痕迹,计算∠α=( )
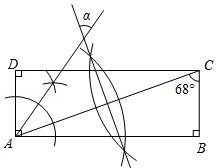 A、56° B、68° C、28° D、34°2. 根据圆规作图的痕迹,可用直尺成功找到三角形内心的是( )A、
A、56° B、68° C、28° D、34°2. 根据圆规作图的痕迹,可用直尺成功找到三角形内心的是( )A、 B、
B、 C、
C、 D、
D、 3. 如图是尺规作图法作 的平分线 时的痕迹图,能判定 的理由是( )
3. 如图是尺规作图法作 的平分线 时的痕迹图,能判定 的理由是( ) A、 B、 C、 D、4. 用尺规作图,已知三边作三角形,用到的基本作图是( )A、作一个角等于已知角 B、作一条线段等于已知线段 C、作已知直线的垂线 D、作角的平分线5. 如图,△ABC中,AC<BC,如果用尺规作图的方法在BC上确定点P,使PA+PC=BC,那么符合要求的作图痕迹是( )
A、 B、 C、 D、4. 用尺规作图,已知三边作三角形,用到的基本作图是( )A、作一个角等于已知角 B、作一条线段等于已知线段 C、作已知直线的垂线 D、作角的平分线5. 如图,△ABC中,AC<BC,如果用尺规作图的方法在BC上确定点P,使PA+PC=BC,那么符合要求的作图痕迹是( )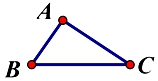 A、
A、 B、
B、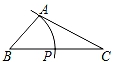 C、
C、 D、
D、 6. 下列三幅图都是“作已知三角形的高”的尺规作图过程,其中作图依据相同的是( )
6. 下列三幅图都是“作已知三角形的高”的尺规作图过程,其中作图依据相同的是( ) A、(1)(2) B、(1)(3) C、(2)(3) D、(1)(2)(3)7. 观察下列作图痕迹, 中, 为 边上的中线是( )A、
A、(1)(2) B、(1)(3) C、(2)(3) D、(1)(2)(3)7. 观察下列作图痕迹, 中, 为 边上的中线是( )A、 B、
B、 C、
C、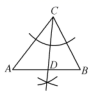 D、
D、 8. 在⊙O中按如下步骤作图:
8. 在⊙O中按如下步骤作图:⑴作⊙O的直径AD;(2)以点D为圆心,DO长为半径画弧,交⊙O于B , C两点;(3)连接DB , DC , AB , AC , BC . 根据以上作图过程及所作图形,下列四个结论中错误的是( )
 A、∠ABD=90° B、∠BAD=∠CBD C、AD⊥BC D、AC=2CD9. 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )A、
A、∠ABD=90° B、∠BAD=∠CBD C、AD⊥BC D、AC=2CD9. 过直线l外一点P作直线l的平行线,下列尺规作图中错误的是( )A、 B、
B、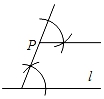 C、
C、 D、
D、 10. 如图,用直尺和圆规作 ,作图痕迹中,弧MN是( )
10. 如图,用直尺和圆规作 ,作图痕迹中,弧MN是( )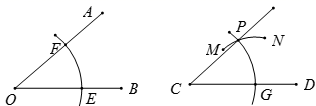 A、以点C为圆心,OE为半径的弧 B、以点C为圆心,EF为半径的弧 C、以点G为圆心,OE为半径的弧 D、以点G为圈心,EF为半径的弧
A、以点C为圆心,OE为半径的弧 B、以点C为圆心,EF为半径的弧 C、以点G为圆心,OE为半径的弧 D、以点G为圈心,EF为半径的弧二、填空题
-
11. 如下框内是“已知一条直角边和斜边作直角三角形”的尺规作图过程.
已知:线段a、b,
求作: 使得斜边 , .
作法:如图.
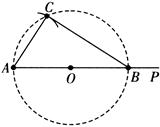
作射线AP,截取线段 ;
以AB为直径,作 ;
以点A为圆心,a的长为半径作弧交 于点C;
连接AC、CB.
即为所求作的直角三角形.
请您写出上述尺规作图的依据:.
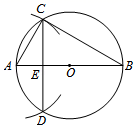
12. 如图,△ABC中,∠B=35°,∠BCA=75°,请依据尺规作图的作图痕迹,计算∠α=°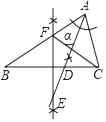 13. 已知⊙O.如图,
13. 已知⊙O.如图,⑴作⊙O的直径AB;
⑵以点A为圆心,AO长为半径画弧,交⊙O于C,D两点;
⑶连接CD交AB于点E,连接AC,BC.
根据以上作图过程及所作图形,有下面三个推断:
①CE=DE; ②BE=3AE; ③BC=2CE.
所有正确推断的序号是 .
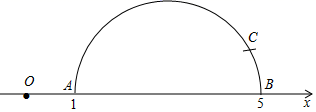
 14. 阅读以下作图过程:
14. 阅读以下作图过程:第一步:在数轴上,点O表示数0,点A表示数1,点B表示数5,以AB为直径作半圆(如图);
第二步:以B点为圆心,1为半径作弧交半圆于点C(如图);
第三步:以A点为圆心,AC为半径作弧交数轴的正半轴于点M.
请你在下面的数轴中完成第三步的画图(保留作图痕迹,不写画法),并写出点M表示的数为 .
 15. 尺规作图特有的魅力曾使无数人沉湎其中,传说拿破仑通过下列尺规作图考他的大臣:
15. 尺规作图特有的魅力曾使无数人沉湎其中,传说拿破仑通过下列尺规作图考他的大臣:
①将半径2的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;
③连结OG.
问:OG的长是多少?大臣给出的正确答案是
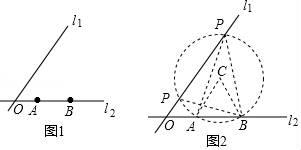
16. 下面是一道确定点P位置的尺规作图题的作图过程.如图1,直线L1与L2相交于点O,A,B是L2上两点,点P是直线L1上的点,且∠APB=30°,请在图中作出符合条件的点P.
作法:如图2,
⑴以AB为边在L2上方作等边△ABC;
⑵以C为圆心,AB长为半径作⊙C交直线L1于P1 , P2两点.则P1、P2就是所作出的符合条件的点P.
请回答:该作图的依据是 .
 17. 如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法),并直接写出旋转角度是 .
17. 如图,已知:BC与CD重合,∠ABC=∠CDE=90°,△ABC≌△CDE,并且△CDE可由△ABC逆时针旋转而得到.请你利用尺规作出旋转中心O(保留作图痕迹,不写作法),并直接写出旋转角度是 . 18. 如图,直线 ,直线 分别与 , 相交于点 、 ,小宇同学利用尺规按以下步骤作图:①以点 为圆心,以任意长为半径作弧交 于点 ,交 于点 ②分别以 , 为圆心,以大于, 长为半径作弧,两弧在 内交于点 ;③作射线 交 于点 ,若 ,则 .
18. 如图,直线 ,直线 分别与 , 相交于点 、 ,小宇同学利用尺规按以下步骤作图:①以点 为圆心,以任意长为半径作弧交 于点 ,交 于点 ②分别以 , 为圆心,以大于, 长为半径作弧,两弧在 内交于点 ;③作射线 交 于点 ,若 ,则 .
三、作图题
-
19. 作图题:小明书上的三角形被墨迹污染了一部分,他想在作业本上用尺规作出一个与书上完全一样的三角形,你能帮他画出来吗?(保留作图痕迹,不写作法)
 20. 已知:两边及其夹角,线段 , , .
20. 已知:两边及其夹角,线段 , , .求作: ,使 , ,(用尺规作图,保留作图痕迹,不写作法).
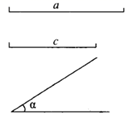
请你根据所学的知识,说明尺规作图作出 ,用到的是三角形全等判定定理中的_▲_,作出的 是唯一的,依据是三角形全等判定定理中的_▲_.
21. 如图,在4×4的方格中,点A,B,C为格点。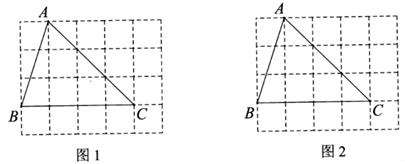 (1)、利用无刻度的直尺在图1中画△ABC的中线BE和重心G;(2)、在图2中标注△ ABC的外心O并画出外接圆及切线CP。22. 如图,在 的方格纸 中,每个小正方形的顶点称为格点.请按要求画图.
(1)、利用无刻度的直尺在图1中画△ABC的中线BE和重心G;(2)、在图2中标注△ ABC的外心O并画出外接圆及切线CP。22. 如图,在 的方格纸 中,每个小正方形的顶点称为格点.请按要求画图.

(1)在图1中画 ,使格点G,H分别在边 , 上,且均不与点A,B,C,D重合.
(2)在图2中,在线段 上找一格点 ,使得 .23. 如图,正方形网格中有一段弧,弧上三点A,B,C均在格点上.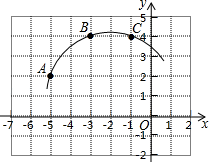 (1)、请作图找出圆心P的位置(保留作图痕迹),并写出它的坐标.(2)、求 的长度.24. 尺规作图:已知△ABC,如图:
(1)、请作图找出圆心P的位置(保留作图痕迹),并写出它的坐标.(2)、求 的长度.24. 尺规作图:已知△ABC,如图: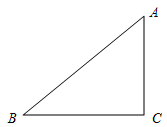 (1)、求作:△ABC的内切圆⊙O;(保留作图痕迹,不写作法)(2)、若∠C=90°,AC=3,AB=4,则△ABC的内切圆⊙O的半径为.25. 如图
(1)、求作:△ABC的内切圆⊙O;(保留作图痕迹,不写作法)(2)、若∠C=90°,AC=3,AB=4,则△ABC的内切圆⊙O的半径为.25. 如图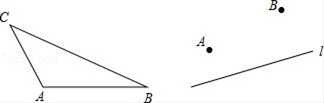 (1)、如图,已知△ABC,请你作出AB边上的高CD,AC边上的中线BE,角平分线AF(不写作法,保留痕迹)(2)、如图,直线l表示一条公路,点A,点B表示两个村庄.现要在公路上造一个车站,并使车站到两个村庄A,B的距离之和最短,问车站建在何处?请在图上标明地点,并说明理由.(要求尺规作图,不写作法)26. 黄金分割为“最美丽”的几何比率,广泛应用于图案设计。下图是一个包装盒的俯视图,线段AB是这个俯视图的中轴线,某公司想在中轴线AB上找到黄金分割点,安装视频播放器。
(1)、如图,已知△ABC,请你作出AB边上的高CD,AC边上的中线BE,角平分线AF(不写作法,保留痕迹)(2)、如图,直线l表示一条公路,点A,点B表示两个村庄.现要在公路上造一个车站,并使车站到两个村庄A,B的距离之和最短,问车站建在何处?请在图上标明地点,并说明理由.(要求尺规作图,不写作法)26. 黄金分割为“最美丽”的几何比率,广泛应用于图案设计。下图是一个包装盒的俯视图,线段AB是这个俯视图的中轴线,某公司想在中轴线AB上找到黄金分割点,安装视频播放器。 (1)、请你用尺规作图的方式找出这个点(作出一点即可,保留作图痕迹);(2)、证明你找到的点是线段AB的黄金分割点。27. 如图所示的直棱柱,其侧棱长为3cm,底面是边长为2cm的等边三角形。
(1)、请你用尺规作图的方式找出这个点(作出一点即可,保留作图痕迹);(2)、证明你找到的点是线段AB的黄金分割点。27. 如图所示的直棱柱,其侧棱长为3cm,底面是边长为2cm的等边三角形。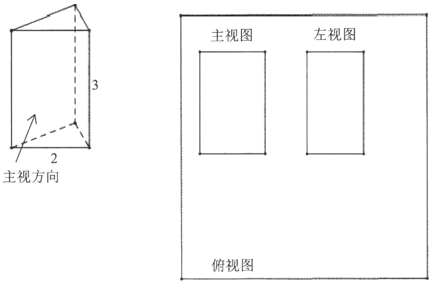 (1)、用尺规作图法补充完整它的三视图(保留作图痕迹,不要求写作法)。(2)、求该直棱柱左视图的面积。28. 若两条线段将一个三角形分割成三个等腰三角形,则这两条线段称为三分线.
(1)、用尺规作图法补充完整它的三视图(保留作图痕迹,不要求写作法)。(2)、求该直棱柱左视图的面积。28. 若两条线段将一个三角形分割成三个等腰三角形,则这两条线段称为三分线.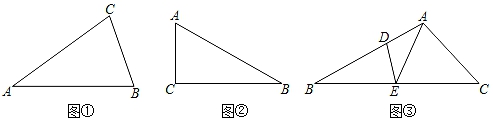 (1)、如图①,△ABC中,AB=AC,∠A=36°,请在图中画出两条三分线,并标出每个等腰三角形顶角的度数(画出一种分割即可).(2)、如图②,△ABC中,∠C=90°,∠A=60°,请在图中画出两条三分线,并标出每个等腰三角形顶角的度数(画出一种分割即可).(3)、如图③,△ABC中,∠BAC为钝角,AE,DE为三分线,BD=BE,DA=DE,CA=CE.
(1)、如图①,△ABC中,AB=AC,∠A=36°,请在图中画出两条三分线,并标出每个等腰三角形顶角的度数(画出一种分割即可).(2)、如图②,△ABC中,∠C=90°,∠A=60°,请在图中画出两条三分线,并标出每个等腰三角形顶角的度数(画出一种分割即可).(3)、如图③,△ABC中,∠BAC为钝角,AE,DE为三分线,BD=BE,DA=DE,CA=CE.①求∠B和∠C的关系式.
②求∠BAC的取值范围.