浙教版备考2021年中考数学三轮冲刺复习专题15 对称与位移
试卷更新日期:2021-05-16 类型:三轮冲刺
一、单选题
-
1. 下列图形中,是中心对称图形但不是轴对称图形的有( )A、
 B、
B、 C、
C、 D、
D、 2. 如图,矩形ABCD中,E是AB的中点,F是AD边上的一个动点,已知AB=4,AD=2 ,△GEF与△AEF关于直线EF成轴对称.当点F沿AD边从点A运动到点D时,点G的运动路径长为( )
2. 如图,矩形ABCD中,E是AB的中点,F是AD边上的一个动点,已知AB=4,AD=2 ,△GEF与△AEF关于直线EF成轴对称.当点F沿AD边从点A运动到点D时,点G的运动路径长为( )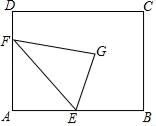 A、2 B、4π C、2π D、3. 已知点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同,则A(a,b)关于x轴对称的点的坐标为( )A、(1,﹣5) B、(1,5) C、(﹣1,5) D、(﹣1,﹣5)4. 如图,是一个三角板,则下列选项中可能是由该图经过一次轴对称变换后得到的是( )
A、2 B、4π C、2π D、3. 已知点P(﹣1﹣2a,5)关于x轴的对称点和点Q(3,b)关于y轴的对称点相同,则A(a,b)关于x轴对称的点的坐标为( )A、(1,﹣5) B、(1,5) C、(﹣1,5) D、(﹣1,﹣5)4. 如图,是一个三角板,则下列选项中可能是由该图经过一次轴对称变换后得到的是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 三角形纸片ABC中,∠C=90°,甲折叠纸片使点A与点B重合,压平得到的折痕长记为m;乙折叠纸片使得CA与CB所在的直线重合,压平得到的折痕长记为n,则m,n的大小关系是( )A、m≤n B、m<n C、m≥n D、m>n6. 如图,矩形 的边 , 分别在坐标轴上,且点 的坐标为 ,将矩形 沿 轴正方向平移 个单位,得到矩形 , 再以点 为旋转中心,把矩形 顺时针方向旋转 ,得到矩形 ″ ″ ″ ″ ″, ″, ″, ″ ,则点 所经过的路线为 ″的长为( )
5. 三角形纸片ABC中,∠C=90°,甲折叠纸片使点A与点B重合,压平得到的折痕长记为m;乙折叠纸片使得CA与CB所在的直线重合,压平得到的折痕长记为n,则m,n的大小关系是( )A、m≤n B、m<n C、m≥n D、m>n6. 如图,矩形 的边 , 分别在坐标轴上,且点 的坐标为 ,将矩形 沿 轴正方向平移 个单位,得到矩形 , 再以点 为旋转中心,把矩形 顺时针方向旋转 ,得到矩形 ″ ″ ″ ″ ″, ″, ″, ″ ,则点 所经过的路线为 ″的长为( ) A、11 B、12 C、4+5 D、4+7. 等腰直角三角形ABC和等腰直角三角形ADE中, , , ,其中 固定, 绕点A顺时针旋转一周,在 旋转过程中,若直线CE与直线BD交点为P,则 面积的最小值为( )
A、11 B、12 C、4+5 D、4+7. 等腰直角三角形ABC和等腰直角三角形ADE中, , , ,其中 固定, 绕点A顺时针旋转一周,在 旋转过程中,若直线CE与直线BD交点为P,则 面积的最小值为( ) A、 B、4 C、 D、4.58. 如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD= ,则 的长为( )
A、 B、4 C、 D、4.58. 如图,将矩形ABCD绕着点A逆时针旋转得到矩形AEFG,点B的对应点E落在边CD上,且DE=EF,若AD= ,则 的长为( )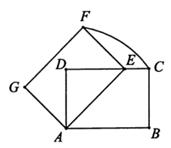 A、 B、 C、 D、π9. 已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则( )A、x=﹣1,y=2 B、x=﹣1,y=8 C、x=﹣1,y=﹣2 D、x=1,y=810. 第一次:将点A绕原点O逆时针旋转90°得到A1;
A、 B、 C、 D、π9. 已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则( )A、x=﹣1,y=2 B、x=﹣1,y=8 C、x=﹣1,y=﹣2 D、x=1,y=810. 第一次:将点A绕原点O逆时针旋转90°得到A1;第二次:作点A1关于x轴的对称点A2;
第三次:将点A2绕点O逆时针旋转90°得到A3;
第四次:作点A3关于x轴的对称点A4…,
按照这样的规律,点A35的坐标是( )
 A、(﹣3,2) B、(﹣2,3) C、(﹣2.﹣3) D、(3.﹣2)
A、(﹣3,2) B、(﹣2,3) C、(﹣2.﹣3) D、(3.﹣2)二、填空题
-
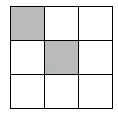
11. 如图,把大正方形平均分成9个小正方形,其中有2个小正方形已被涂黑,在剩余的7个白色小正方形中任选一个也涂黑,则使整个涂黑部分成为轴对称图形的概率是 .
 12. 如图,在矩形ABCD中,AB=12,BC=16,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则DF的长为
12. 如图,在矩形ABCD中,AB=12,BC=16,点E是BC中点,点F是边CD上的任意一点,当△AEF的周长最小时,则DF的长为 13. 已知图中Rt△ABC,∠B=90°,AB=BC,斜边AC上的一点D,满足AD=AB,将线段AC绕点A逆时针旋转α (0°<α <360°),得到线段ac’,连接dc’,当dc’ bc时,旋转角度α 的值为 ,
13. 已知图中Rt△ABC,∠B=90°,AB=BC,斜边AC上的一点D,满足AD=AB,将线段AC绕点A逆时针旋转α (0°<α <360°),得到线段ac’,连接dc’,当dc’ bc时,旋转角度α 的值为 ,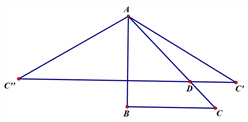 14. 如图,在△ABC中,∠ACB为钝角,把边AC绕点A沿逆时针方向旋转90°得AD,把边BC绕点B沿顺时针方向旋转90°得BE,作DM⊥AB于点M,EN⊥AB于点N,若AB=5,EN=2,则DM=.
14. 如图,在△ABC中,∠ACB为钝角,把边AC绕点A沿逆时针方向旋转90°得AD,把边BC绕点B沿顺时针方向旋转90°得BE,作DM⊥AB于点M,EN⊥AB于点N,若AB=5,EN=2,则DM=. 15. 如图,矩形ABCD周长为30,经过矩形对称中心O的直线分别交AD,BC于点E,F.将矩形沿直线EF翻折,A′B′分别交AD,CD于点M,N,B′F交CD于点G.若MN:EM=l:2,则△DMN的周长为.
15. 如图,矩形ABCD周长为30,经过矩形对称中心O的直线分别交AD,BC于点E,F.将矩形沿直线EF翻折,A′B′分别交AD,CD于点M,N,B′F交CD于点G.若MN:EM=l:2,则△DMN的周长为.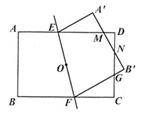 16. 在平面直角坐标系中,点P(2,m)绕坐标原点O逆时针旋转 后,恰好落在图中阴影区域(包括边界)内,则m的取值范围是 .
16. 在平面直角坐标系中,点P(2,m)绕坐标原点O逆时针旋转 后,恰好落在图中阴影区域(包括边界)内,则m的取值范围是 .
三、综合题
-
17. 如图,在下列5×5的网格中,横、纵坐标均为整点的数叫做格点,例如(0,1)、B(2,1)、C(3,3)都是格点,现仅用无刻度的直尺在网格中做如下操作:
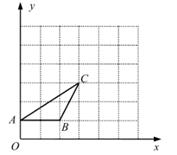
( 1 )直接写出点A关于点B旋转180°后对应点M的坐标 ▲ ;
( 2 )画出线段BE,使BE⊥AC,其中E是格点,并写出点E的坐标 ▲ ;
( 3 )找格点F,使∠EAF=∠CAB,画出∠EAF,并写出点F的坐标 ▲ 。
18. 如图,在平面直角坐标系中,点 ,点 ,点 . (1)、画出 关于 轴的对称图形 ,并写出点 的对称点 的坐标;(2)、若点 在 轴上,连接 、 ,则 的最小值是;
(1)、画出 关于 轴的对称图形 ,并写出点 的对称点 的坐标;(2)、若点 在 轴上,连接 、 ,则 的最小值是;
(3)、若直线 轴,与线段 、 分别交于点 、 (点 不与点 重合),若将 沿直线 翻折,点 的对称点为点 ,当点 落在 的内部(包含边界)时,点 的横坐标 的取值范围是.
19. 如图,在直角坐标系中,长方形 的三个顶点的坐标为 , , ,且 轴,点 是长方形内一点(不含边界).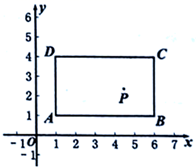 (1)、求a,b的取值范围.(2)、若将点P向左移动8个单位,再向上移动2个单位到点Q,若点Q恰好与点C关于 轴对称,求a,b的值.20. 已知一张正方形ABCD纸片,边长AB=2,按步骤进行折叠,如图1,先将正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF.
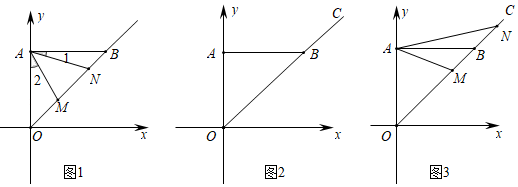
(1)、求a,b的取值范围.(2)、若将点P向左移动8个单位,再向上移动2个单位到点Q,若点Q恰好与点C关于 轴对称,求a,b的值.20. 已知一张正方形ABCD纸片,边长AB=2,按步骤进行折叠,如图1,先将正方形纸片ABCD对折,得到折痕EF;再折出矩形BCFE的对角线BF. (1)、如图2,将CF边折到BF上,得到折痕FM,点C的对应点为C',求CM的长.(2)、如图3,将AB边折到BF上,得到折痕BN,点A的对应点为A',求AN的长.21. 在平面直角坐标系中,已知点A(0,4),B(4,4),点M,N是射线OC上两动点(OM<ON),且运动过程中始终保持∠MAN=45°,小明用几何画板探究其中的线段关系.(1)、探究发现:当点M,N均在线段OB上时(如图1),有OM2+BN2=MN2.
(1)、如图2,将CF边折到BF上,得到折痕FM,点C的对应点为C',求CM的长.(2)、如图3,将AB边折到BF上,得到折痕BN,点A的对应点为A',求AN的长.21. 在平面直角坐标系中,已知点A(0,4),B(4,4),点M,N是射线OC上两动点(OM<ON),且运动过程中始终保持∠MAN=45°,小明用几何画板探究其中的线段关系.(1)、探究发现:当点M,N均在线段OB上时(如图1),有OM2+BN2=MN2.他的证明思路如下:
第一步:将△ANB绕点A顺时针旋转90°得△APO,连结PM,则有BN=OP.
第二步:证明△APM≌△ANM,得MP=MM.
第一步:证明∠POM=90°,得OM2+OP2=MP2.
最后得到OM2+BN2=MN2.
请你完成第二步三角形全等的证明.
 (2)、继续探究:除(1)外的其他情况,OM2+BN2=MN2的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)、新题编制:若点B是MN的中点,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).22. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y= (k>0,x>0)的图象上,点D的坐标为( ,2)。
(2)、继续探究:除(1)外的其他情况,OM2+BN2=MN2的结论是否仍然成立?若成立,请证明;若不成立,请说明理由.(3)、新题编制:若点B是MN的中点,请你编制一个计算题(不标注新的字母),并直接给出答案(根据编出的问题层次,给不同的得分).22. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y= (k>0,x>0)的图象上,点D的坐标为( ,2)。 (1)、求k的值;(2)、若将菱形ABCD沿x轴正方向平移, 当菱形的另一个顶点恰好落在函数y= (k>0,x>0)的图象上时,求菱形ABCD平移的距离。23. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.
(1)、求k的值;(2)、若将菱形ABCD沿x轴正方向平移, 当菱形的另一个顶点恰好落在函数y= (k>0,x>0)的图象上时,求菱形ABCD平移的距离。23. 如图1是实验室中的一种摆动装置,BC在地面上,支架ABC是底边为BC的等腰直角三角形,摆动臂AD可绕点A旋转,摆动臂DM可绕点D旋转,AD=30,DM=10.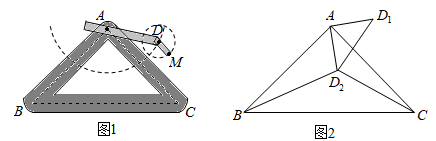 (1)、在旋转过程中,
(1)、在旋转过程中,①当A,D,M三点在同一直线上时,求AM的长。
②当A,D,M三点为同一直角三角形的顶点时,求AM的长。
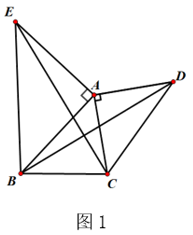
(2)、若摆动臂AD顺时针旋转90°,点D的位置由△ABC外的点D1转到其内的点D2处,连结D1D2 , 如图2.此时∠AD2C=135°,CD2=60,求BD2的长.24. 如图(1)、【问题探究】如图1,锐角△ABC中,分别以AB、AC为边向外作等腰直角△ABE和等腰直角△ACD,使AE=AB,AD=AC,∠BAE=∠CAD=90°,连接BD,CE,试猜想BD与CE的大小关系,不需要证明.
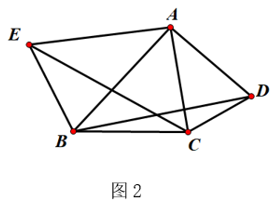
 (2)、【深入探究】
(2)、【深入探究】如图2,锐角△ABC中分别以AB、AC为边向外作等腰△ABE和等腰△ACD,使AE=AB,AD=AC,∠BAE=∠CAD,连接BD、CE,试猜想BD与CE的大小关系,并说明理由.
 (3)、【拓展应用】
(3)、【拓展应用】如图3,在△ABC中,∠ACB=45°,以AB为直角边,A为直角顶点向外作等腰直角△ABD,连接CD,若AC= ,BC=3,则CD长为.
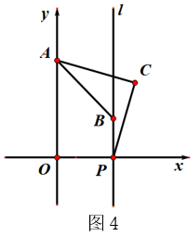
 (4)、如图4,已知在平面直角坐标系xOy中,O为坐标原点,A(0, )、P(3,0),过点P作直线l⊥x轴,点B是直线l上的一个动点,线段AB绕点A按逆时针方向旋转30°得到线段AC.则AC+PC的最小值为 .
(4)、如图4,已知在平面直角坐标系xOy中,O为坐标原点,A(0, )、P(3,0),过点P作直线l⊥x轴,点B是直线l上的一个动点,线段AB绕点A按逆时针方向旋转30°得到线段AC.则AC+PC的最小值为 .