浙教版备考2021年中考数学三轮冲刺复习专题12 反比例函数
试卷更新日期:2021-05-16 类型:三轮冲刺
一、单选题
-
1. 面积为4的矩形的长为x,宽为y,则y与x的函数关系的图象大致是( )A、
 B、
B、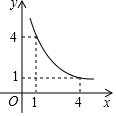 C、
C、 D、
D、 2. 已知反比例函数y= 的图象在每一个象限内,y随x的增大而增大,那么一次函数y=kx+2的大致图象是( )A、
2. 已知反比例函数y= 的图象在每一个象限内,y随x的增大而增大,那么一次函数y=kx+2的大致图象是( )A、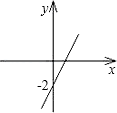 B、
B、 C、
C、 D、
D、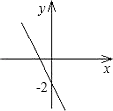 3. 已知函数y= ,下列说法:
3. 已知函数y= ,下列说法:①函数图象分布在第一、三象限;②在每个象限内,y随x的增大而减小;③若A(x1 , y1)、B(x2 , y2)两点在该图象上,且x1+x2=0,则y1=y2。其中说法正确的个数是( )
A、0 B、1 C、2 D、34. 已知函数y=- 的图象上有三点A(x1 , y1),B(x2 , y2),C(x3 , y3),且x1<x2<0<x3;则y1 , y2 , y3的大小关系为( )。A、y1<y2<y3 B、y3<y1<y2 C、y2<y1<y3 D、y2<y3<y15. 如图,在平面直角坐标系中,点P(1,4)、Q(m,n)在函数y= (k>0)的图象上,当m>1时,过点P分别作x轴、y轴的垂线,垂足为点A,B;过点Q分别作x轴、y轴的垂线,垂足为点C,D,QD交PA于点E,随着m的增大,四边形ACQE的面积( )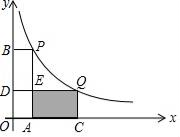 A、增大 B、减小 C、先减小后增大 D、先增大后减小6. 已知:如图,在平面直角坐标系 中,等边 的边长为6,点C在边 上,点D在边 上,且 .反比例函数 的图象恰好经过点C和点D.则k的值为 ( )
A、增大 B、减小 C、先减小后增大 D、先增大后减小6. 已知:如图,在平面直角坐标系 中,等边 的边长为6,点C在边 上,点D在边 上,且 .反比例函数 的图象恰好经过点C和点D.则k的值为 ( )
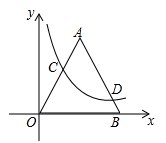 A、 B、 C、 D、7. 如图,一次函数与反比例函数的图象交于A(1,8)和B(4,2)两点,点P是线段AB上一动点(不与点A和B重合),过P点分别作x轴,y轴的垂线PC,PD交反比例函数图象于点E,F,则四边形OEPF面积的最大值是( )
A、 B、 C、 D、7. 如图,一次函数与反比例函数的图象交于A(1,8)和B(4,2)两点,点P是线段AB上一动点(不与点A和B重合),过P点分别作x轴,y轴的垂线PC,PD交反比例函数图象于点E,F,则四边形OEPF面积的最大值是( ) A、3 B、4 C、 D、68. 在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(mm)与面条的粗细s(mm²)(横截面积)的对应数据如下表.根据表中数据,可得y关于s的函数表达式为( )
A、3 B、4 C、 D、68. 在做拉面的过程中渗透着数学知识:一定体积的面团做成拉面,面条的总长度y(mm)与面条的粗细s(mm²)(横截面积)的对应数据如下表.根据表中数据,可得y关于s的函数表达式为( )面条的总长度y(mm)
100
200
400
800
2000
面条的粗细s(mm2)
12.80
6.40
3.20
1.60
0.64
A、y= B、y= C、y= D、y=9. 如图,Rt△AOB中,∠AOB=90°,顶点A,B分别在反比例函数y= (x>0)与y= (x<0)的图象上,则下列等式成立的是( )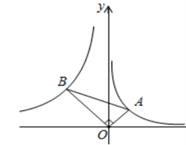 A、sin∠ BAO= B、cos∠BAO= C、tan∠BAO=2 D、sin∠ABO=10. 如图所示,为A,E在反比例函数y= (x>0)的图象上,点B,D在反比例函数y= (k>0) 的图象上,AB∥DE∥y轴,连结DA并延长交y轴于点C,CD∥x轴,△ABC与△ADE的面积之差为 ,则k的值为( )
A、sin∠ BAO= B、cos∠BAO= C、tan∠BAO=2 D、sin∠ABO=10. 如图所示,为A,E在反比例函数y= (x>0)的图象上,点B,D在反比例函数y= (k>0) 的图象上,AB∥DE∥y轴,连结DA并延长交y轴于点C,CD∥x轴,△ABC与△ADE的面积之差为 ,则k的值为( )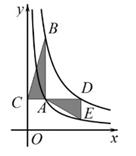 A、4 B、5 C、6 D、8
A、4 B、5 C、6 D、8二、填空题
-
11. 已知平面直角坐标系xOy,正方形OABC,点B(4,4),过边BC上动点P(不含端点C)的反比例函数 的图象交AB边于Q点,连结PQ,若把横、纵坐标均为整数的点叫做好点,则反比例函数图象与线段PQ围成的图形(含边界)中好点个数为三个时,k的取值范围为.
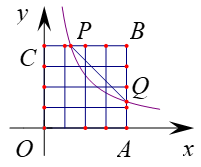 12. 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(4,4),C(﹣2,﹣2),点B,D在反比例函数 的图象上,对角线BD交AC于点M,交x轴于点N,若 ,则k的值是.
12. 如图,在平面直角坐标系xOy中,菱形ABCD的顶点A(4,4),C(﹣2,﹣2),点B,D在反比例函数 的图象上,对角线BD交AC于点M,交x轴于点N,若 ,则k的值是.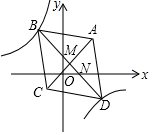 13. 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y= (k≠0)在第一象限的图象过点A(m,2)和CD边上一点E(n,1),则△EOC的面积是.
13. 如图,正方形ABCD的顶点B,C在x轴的正半轴上,反比例函数y= (k≠0)在第一象限的图象过点A(m,2)和CD边上一点E(n,1),则△EOC的面积是.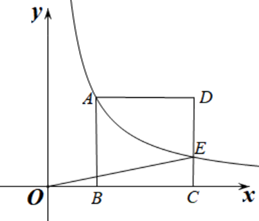 14. 已知一次函数y1=(k-1)x+3和反比例函数y2= ,当-2<x<0时,y1>y2恒成立,则k的取值范围。15. 如图,直线y=ax+b与反比例函数y= (c<0)的图象交于A,B两点,在反比例函数y= (d>0)图象的第一象限分支上取一点C,若△ABC是以原点O为重心的等边三角形,则 的值为.
14. 已知一次函数y1=(k-1)x+3和反比例函数y2= ,当-2<x<0时,y1>y2恒成立,则k的取值范围。15. 如图,直线y=ax+b与反比例函数y= (c<0)的图象交于A,B两点,在反比例函数y= (d>0)图象的第一象限分支上取一点C,若△ABC是以原点O为重心的等边三角形,则 的值为.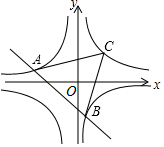 16. 如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M。反比例函数y= (x>0)的图象恰好经过点F,M。若直尺的宽CD=3,三角板的斜边FG=8 ,则k=。
16. 如图,将一把矩形直尺ABCD和一块含30°角的三角板EFG摆放在平面直角坐标系中,AB在x轴上,点G与点A重合,点F在AD上,三角板的直角边EF交BC于点M。反比例函数y= (x>0)的图象恰好经过点F,M。若直尺的宽CD=3,三角板的斜边FG=8 ,则k=。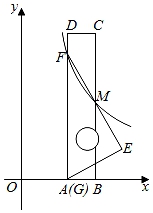
三、综合题
-
17. 已知点A(x1 , y1),B(x2 , y2)是反比例函数y= (k≠0)图象上两点。(1)、若点A,B关于原点中心对称,求5x1y2-7x2y1的值(则用含k的代数式表示)。(2)、设x1=a-1,x2=a+1,若y1<y2 , 求a的取值范围。18. 已知一次函数y1=3x-3的图象与反比例函数y2= 的图象交于点A(a,3),B(-1,b)。(1)、求a,b的值和反比例函数的表达式;(2)、设点P(h,y1),Q(h,y2)分别是两函数图象上的点;
①试直接写出当y1>y2时h的取值范围;
②若y2-y1=3,试求h的值。
19. 参照学习函数的过程与方法,探究函数y= 的图象与性质.因为y= ,即y=﹣ +1,所以我们对比函数y=﹣ 来探究.
列表:
x
…
﹣4
﹣3
﹣2
﹣1
﹣
1
2
3
4
…
y=﹣
…
1
2
4
﹣4
﹣2
﹣1
﹣
﹣
…
y=
…
2
3
5
﹣3
﹣1
0
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以y= 相应的函数值为纵坐标,描出相应的点,如图所示:
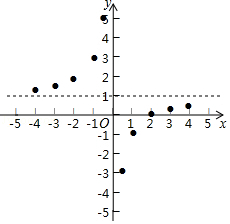 (1)、请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;(2)、观察图象并分析表格,回答下列问题:
(1)、请把y轴左边各点和右边各点,分别用一条光滑曲线顺次连接起来;(2)、观察图象并分析表格,回答下列问题:①当x<0时,y随x的增大而;(填“增大”或“减小”)
②y= 的图象是由y=﹣ 的图象向平移个单位而得到;
③图象关于点中心对称.(填点的坐标)
(3)、设A(x1 , y1),B(x2 , y2)是函数y= 的图象上的两点,且x1+x2=0,试求y1+y2+3的值.20. 如图,正六边形ABCDEF的对称中心P在反比例函数y= (k>0,x>0)的图象上边CD在x轴上,点B在y轴上,已知CD=4.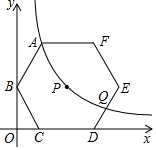 (1)、点A是否在该反比例函数的图象上?请说明理由.
(1)、点A是否在该反比例函数的图象上?请说明理由.
(2)、若该反比例函数图象与DE交于点Q,求点Q的横坐标;
(3)、平移正六边形ABCDEF,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
21. 如图所示,M、N、P在第二象限,横坐标分别是﹣4、﹣2、﹣1,双曲线y= 过M、N、P三点,且MN=NP.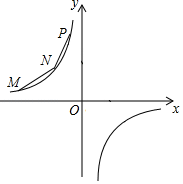 (1)、求双曲线的解析式;(2)、过P点的直线l交x轴于A,交y轴于B,且PA=4AB,且交y= 于另一点Q,求Q点坐标;(3)、以PN为边(顺时针方向)作正方形PNEF,平移正方形使N落在x轴上,点P、E对应的点P′、E'正好落在反比例函数y= 上,求F对应点F′的坐标.22. 某游泳池毎次换水前后水的体积基本保持不变,当该游泳池以每小时300立方米的速度放水时,经3小时能将池内的水放完.设放水的速度为x立方米/时,将池内的水放完需y小时.已知该游泳池毎小时的最大放水速度为350立方米(1)、求y关于x的函数表达式.(2)、若该游泳池将放水速度控制在每小时200立方米至250立方米(含200立方米和250立方米),求放水时间y的范围.(3)、该游泳池能否在2.5小时内将池内的水放完?请说明理由.23. 如图,点A,B分别在x轴,y轴上,过A,B作AB垂线,交反比例函数y= (k>0,x>0)的图象于D,C,四边形ABCD为矩形,CF⊥y轴于F,DE⊥x轴于E,CF=a,BF=b,OA=x,OB=y.
(1)、求双曲线的解析式;(2)、过P点的直线l交x轴于A,交y轴于B,且PA=4AB,且交y= 于另一点Q,求Q点坐标;(3)、以PN为边(顺时针方向)作正方形PNEF,平移正方形使N落在x轴上,点P、E对应的点P′、E'正好落在反比例函数y= 上,求F对应点F′的坐标.22. 某游泳池毎次换水前后水的体积基本保持不变,当该游泳池以每小时300立方米的速度放水时,经3小时能将池内的水放完.设放水的速度为x立方米/时,将池内的水放完需y小时.已知该游泳池毎小时的最大放水速度为350立方米(1)、求y关于x的函数表达式.(2)、若该游泳池将放水速度控制在每小时200立方米至250立方米(含200立方米和250立方米),求放水时间y的范围.(3)、该游泳池能否在2.5小时内将池内的水放完?请说明理由.23. 如图,点A,B分别在x轴,y轴上,过A,B作AB垂线,交反比例函数y= (k>0,x>0)的图象于D,C,四边形ABCD为矩形,CF⊥y轴于F,DE⊥x轴于E,CF=a,BF=b,OA=x,OB=y.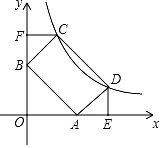 (1)、求证:AE=a.(2)、请写出两个不同的关于a,b,x,y的关系式.(3)、求证:∠OAB=45°.24. 城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系xOy,对两点A(x1 , y1)和B(x2 , y2),用以下方式定义两点间距离:d(A,B)=|x1﹣x2|+|y1﹣y2|.
(1)、求证:AE=a.(2)、请写出两个不同的关于a,b,x,y的关系式.(3)、求证:∠OAB=45°.24. 城市的许多街道是相互垂直或平行的,因此,往往不能沿直线行走到达目的地,只能按直角拐弯的方式行走.可以按照街道的垂直和平行方向建立平面直角坐标系xOy,对两点A(x1 , y1)和B(x2 , y2),用以下方式定义两点间距离:d(A,B)=|x1﹣x2|+|y1﹣y2|.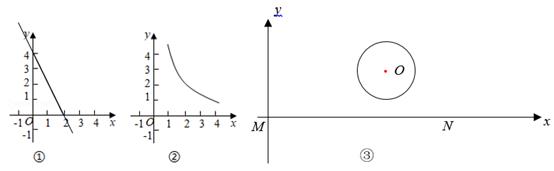 (1)、【数学理解】
(1)、【数学理解】①已知点A(-2,1),则d(O,A)=.
②函数y=-2x+4的图象如图①所示,B是图象上一点,d(O,B)=3,则点B的坐标是.
(2)、函数y= (x>0)的图象如图②所示.求证:该函数图象上不存在点C,使d(O,C)=3.(3)、【问题解决】某市要修建一条通往一圆形景观湖的道路,如图③,道路以M为起点,先沿MN方向到某处,再在该处拐一次直角弯沿直线到湖边某点P处,如图建立坐标系,圆心O(5,3),半径为 ,求修建道路距离d(O,P)的取值范围.