浙教版备考2021年中考数学三轮冲刺复习专题11 函数与坐标系
试卷更新日期:2021-05-16 类型:三轮冲刺
一、单选题
-
1. 已知点(m,﹣2)关于原点对称的点落在直线y=x﹣3上,则m的值为( )A、﹣5 B、﹣2 C、1 D、22. 已知点P(m+2,2m-4)在y轴上,则点P的坐标是( )A、(8,0) B、(0,-8) C、(-8,0) D、(0,8)3. 下列四个备选项中,其中有一个选项的内容从表达形式上看不属于函数,则这一个选项是( )A、y= B、y=3x+1 C、y=-2x²+x-1 D、4. 张老师出门散步时离家的距离y与时间x之间的函数图象如图所示,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )
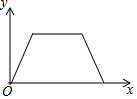 A、
A、 B、
B、 C、
C、 D、
D、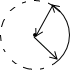 5. 已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1 , y2 , 0的大小关系是( )A、0<y1<y2 B、y1<0<y2 C、y1<y2<0 D、y2<0<y16. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、
5. 已知点(﹣1,y1),(4,y2)在一次函数y=3x﹣2的图象上,则y1 , y2 , 0的大小关系是( )A、0<y1<y2 B、y1<0<y2 C、y1<y2<0 D、y2<0<y16. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、 B、
B、 C、
C、 D、
D、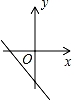 7. 在平面直角坐标系中,若点A(1,m)到原点的距离小于或等于5,则m的取值范围是( )A、0≤m≤2 B、0≤m≤ C、 ≤m≤ D、-2 ≤m≤28. 两条直线y1=ax-b与y2=bx-a在同一坐标系中的图象可能是图中的( )A、
7. 在平面直角坐标系中,若点A(1,m)到原点的距离小于或等于5,则m的取值范围是( )A、0≤m≤2 B、0≤m≤ C、 ≤m≤ D、-2 ≤m≤28. 两条直线y1=ax-b与y2=bx-a在同一坐标系中的图象可能是图中的( )A、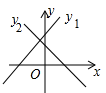 B、
B、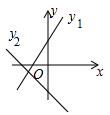 C、
C、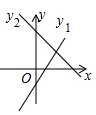 D、
D、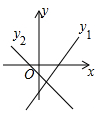 9. 若正比例函数y=kx的图象经过一、三象限,且过点A(2a,4)和B(2,a),则k的值为( )A、﹣2 B、2 C、﹣1 D、110. 如图,点C的坐标为(3,4),CA⊥y轴于点A,D是线段AO上一点,且OD=3AD,点B从原点O出发,沿x轴正方向运动,CB与直线y= x交于点E,则△CDE的面积( )
9. 若正比例函数y=kx的图象经过一、三象限,且过点A(2a,4)和B(2,a),则k的值为( )A、﹣2 B、2 C、﹣1 D、110. 如图,点C的坐标为(3,4),CA⊥y轴于点A,D是线段AO上一点,且OD=3AD,点B从原点O出发,沿x轴正方向运动,CB与直线y= x交于点E,则△CDE的面积( )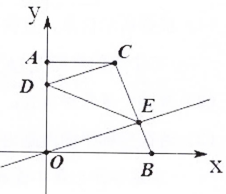 A、逐渐变大 B、先变大后变小 C、逐渐变小 D、始终不变
A、逐渐变大 B、先变大后变小 C、逐渐变小 D、始终不变二、填空题
-
11. 把直线 绕原点旋转180 ,所得直线的解析式为.12. 在平面直角坐标系xOy中,我们把横、纵坐标都是整数的点叫做整点,已知点A(0,4),点B是x轴正半轴上的整点,记△AOB内部(不包括边界)的整点个数为m,当m=3时,则点B的横坐标是 .
 13. 某函数满足当自变量x=-1时,函数的值y=2,且函数y的值始终随自变量x的增大而减小,写出一个满足条件的函数表达式 .14. 某油箱容量为50L的汽车,加满汽油后开了200km时,油箱中的汽油大约消耗了 如果加满汽油后汽车行驶的路程为xkm,油箱中的剩油量为yL,则y与x之间的函数关系式和自变量取值范围分别是.
13. 某函数满足当自变量x=-1时,函数的值y=2,且函数y的值始终随自变量x的增大而减小,写出一个满足条件的函数表达式 .14. 某油箱容量为50L的汽车,加满汽油后开了200km时,油箱中的汽油大约消耗了 如果加满汽油后汽车行驶的路程为xkm,油箱中的剩油量为yL,则y与x之间的函数关系式和自变量取值范围分别是.
15. 已知直线y1=kx+1(k<0)与直线y2=nx(n>0)的交点坐标为( , ),则不等式组nx-3<kx+1<nx的解集为.16. 如图,平面直角坐标系中有三点A(6,4)、B(4,6)、C(0,2),在x轴上找一点D,使得四边形ABCD的周长最小,则点D的坐标应该是 .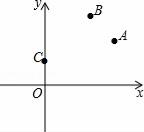 17. 如图,在平面直角坐标系中,点A1的坐标为(1,0),以OA1为直角边作Rt△OA1A2 , 并使∠A1OA2=60°,再以OA2为直角边作Rt△OA2A3 , 并使∠A2OA3=60°,再以OA3为直角边作Rt△OA3A4 , 并使∠A3OA4=60°…按此规律进行下去,则点A2019的坐标为.
17. 如图,在平面直角坐标系中,点A1的坐标为(1,0),以OA1为直角边作Rt△OA1A2 , 并使∠A1OA2=60°,再以OA2为直角边作Rt△OA2A3 , 并使∠A2OA3=60°,再以OA3为直角边作Rt△OA3A4 , 并使∠A3OA4=60°…按此规律进行下去,则点A2019的坐标为. 18. 如图,在平面直角坐标系中,一次函数
18. 如图,在平面直角坐标系中,一次函数 的图象与 轴和 轴分别相交于 A 、 B 两点.动点 P 从点 A 出发,在线段
的图象与 轴和 轴分别相交于 A 、 B 两点.动点 P 从点 A 出发,在线段  上以每秒3个单位长度的速度向点 作匀速运动,到达点 停止运动,点 A 关于点 P 的对称点为点 Q ,以线段 为边向上作正方形
上以每秒3个单位长度的速度向点 作匀速运动,到达点 停止运动,点 A 关于点 P 的对称点为点 Q ,以线段 为边向上作正方形  .设运动时间为 t 秒.若正方形
.设运动时间为 t 秒.若正方形  对角线的交点为 T ,则
对角线的交点为 T ,则  的最小值为 .
的最小值为 . 
三、综合题
-
19. 设一次函数y=ax+b(a,b是常数,且a≠0)的图象A(1,3)和B(-1,-1)两点.(1)、求该一次函数的表达式.(2)、①若点( ,2)在(1)中的函数图象上,求m的值.
②若(1)中的函数图象和y=-2x+n的函数图象的交点在第一象限,求n的取值范围.
20. 某手机专卖店销售A,B两种型号的手机,如表是近两周的销售情况:销售时段
销售数量
销售利润
A型
B型
第一周
3台
5台
1800元
第二周
4台
10台
3000元
(1)、求每台A型手机和B型手机的销售利润;(2)、该手机专卖店计划一次购进两种型号的手机共100台,其中A型号手机的进货量不超过B型号手机进货量的2倍.设购进A型号手机x台,这100台手机的销售总利润为y元.①求y关于x的函数表达式;
②该商店购进A型号和B型号手机各多少台,才能使销售总利润最大?
(3)、实际进货时,厂家对A型号手机的出厂价提高a(0<a<100)元,对B型号手机的出厂价下降a(0<a<100)元,且限定该手机专卖店至少购进A型号手机20台.若该手机专卖店保持两种手机的售价不变,请根据以上信息及(2)中条件,设计出使这100台手机销售总利润最大的进货方案.21. 在平面直角坐标系xOy中,直线l1:y=k1x+2 与x轴、y轴分别交于点A、B两点,OA= OB,直线l2:y=k2x+b经过点C(1,﹣ ),与x轴、y轴和线段AB分别交于点E、F、D三点. (1)、求直线l1的解析式;(2)、如图①:若EC=ED,求点D的坐标和△BFD的面积;(3)、如图②:在坐标轴上是否存在点P,使△PCD是以CD为底边的等腰直角三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.22. 现要把228吨物资从某地运往甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如表:
(1)、求直线l1的解析式;(2)、如图①:若EC=ED,求点D的坐标和△BFD的面积;(3)、如图②:在坐标轴上是否存在点P,使△PCD是以CD为底边的等腰直角三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.22. 现要把228吨物资从某地运往甲、乙两地,用大、小两种货车共18辆,恰好能一次性运完这批物资.已知这两种货车的载重量分别为16吨/辆和10吨/辆,运往甲、乙两地的运费如表:运往地
车 型
甲 地(元/辆)
乙 地(元/辆)
大货车
720
800
小货车
500
650
(1)、求这两种货车各用多少辆?(2)、如果安排9辆货车前往甲地,其余货车前往乙地,设前往甲地的大货车为a辆,前往甲、乙两地的总运费为w元,求出w与a的函数关系式(写出自变量的取值范围);(3)、在(2)的条件下,若运往甲地的物资不少于120吨,请你设计出使总运费最少的货车调配方案,并求出最少总运费.23. 如图,在平面直角坐标系中,过点A 的直线l分别与x轴、y轴交于点C,D.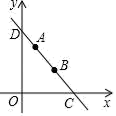 (1)、求直线l的函数表达式.(2)、P为x轴上一点,若△PCD为等腰三角形直接写出点P的坐标.(3)、将线段AB绕B点旋转90°,直接写出点A对应的点A的坐标.24. 如图1是两圆柱形连通容器,两根铁棒直立于甲容器底部(连通处及铁棒体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)与时间t(分)的函数关系如图2所示.已知两根铁棒的长度之和为34cm,当水面达到连通处时,一根露出水面的长度是它的 ,另一根露出水面的长度是它的 .
(1)、求直线l的函数表达式.(2)、P为x轴上一点,若△PCD为等腰三角形直接写出点P的坐标.(3)、将线段AB绕B点旋转90°,直接写出点A对应的点A的坐标.24. 如图1是两圆柱形连通容器,两根铁棒直立于甲容器底部(连通处及铁棒体积忽略不计),向甲容器匀速注水,甲容器的水面高度h(cm)与时间t(分)的函数关系如图2所示.已知两根铁棒的长度之和为34cm,当水面达到连通处时,一根露出水面的长度是它的 ,另一根露出水面的长度是它的 . (1)、①图2中(3,a)表示的实际意义是 ▲ ;
(1)、①图2中(3,a)表示的实际意义是 ▲ ;②请求出a的值;
(2)、若甲、乙两容器的底面积之比为S甲 , S乙=3:2.①直接写出b的值为 ▲ ;
②求点P的坐标.
25. 如图,在平面直角坐标系中,直线y=kx+b与x轴交于点A(5,0),与y轴交于点B;直线y═ x+6过点B和点C,且AC⊥x轴.点M从点B出发以每秒2个单位长度的速度沿y轴向点O运动,同时点N从点A出发以每秒3个单位长度的速度沿射线AC向点C运动,当点M到达点O时,点M、N同时停止运动,设点M运动的时间为t(秒),连接MN.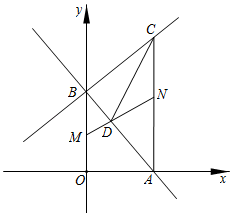 (1)、求直线y=kx+b的函数表达式及点C的坐标;(2)、当MN∥x轴时,求t的值;(3)、MN与AB交于点D,连接CD,在点M、N运动过程中,线段CD的长度是否变化?如果变化,请直接写出线段CD长度变化的范围;如果不变化,请直接写出线段CD的长度.26. 已知:直线 和 ( 且 )交于点 .(1)、若点 的横坐标为2,求 的值.(2)、若直线 经过第四象限,求直线 所经过的象限.(3)、点 在直线 上,点 在直线 上,当 时,始终有 ,求 的取值范围.
(1)、求直线y=kx+b的函数表达式及点C的坐标;(2)、当MN∥x轴时,求t的值;(3)、MN与AB交于点D,连接CD,在点M、N运动过程中,线段CD的长度是否变化?如果变化,请直接写出线段CD长度变化的范围;如果不变化,请直接写出线段CD的长度.26. 已知:直线 和 ( 且 )交于点 .(1)、若点 的横坐标为2,求 的值.(2)、若直线 经过第四象限,求直线 所经过的象限.(3)、点 在直线 上,点 在直线 上,当 时,始终有 ,求 的取值范围.