浙教版备考2021年中考数学三轮冲刺复习专题9 三角形
试卷更新日期：2021-05-16 类型：三轮冲刺
一、单选题
-
1. 如图，将直角三角形ABC（∠BAC＝90°）绕点A逆时针旋转一定角度得到直角三角形ADE，若∠CAE＝65°，若∠AFB＝90°，则∠D的度数为（ ）
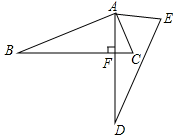A、60° B、35° C、25° D、15°2. 在周长为25的三角形中，最短边是x，另一边是2x﹣3，则x的取值范围（ ）
A、 ＜x＜ B、 ＜x＜7 C、3≤x≤7 D、3＜x＜73. G为△ABC的重心，△ABC的三边长满足AB＞BC＞CA，记△GAB，△GBC，△GCA的面积分别为S1、S2、S3 ， 则有（ ）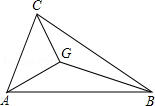
A、S1＞S2＞S3 B、S1＝S2＝S3 C、S1＜S2＜S3 D、S1、S2、S3的大小关系不确定4. 在△ABC中，D是BC边上的点（不与B，C重合），连接AD，下列表述错误的是（ ）A、若AD是BC边的中线，则BC＝2CD B、若AD是BC边的高线，则AD＜AC C、岩AD是∠BAC的平分线，则△ABD与△ACD的面积相等 D、若AD是∠BAC的平分线又是BC边的中线，则AD为BC边的高线5. 如图，把△ABC纸片的∠A沿DE折叠，点A落在四边形CBDE外，则∠1、∠2与∠A的关系是（ ）
A、∠1+∠2＝2∠A B、∠2﹣∠A＝2∠1 C、∠2﹣∠1＝2∠A D、∠1+∠A＝ ∠26. 如图，△ABC中，AB=BC，AD⊥BC于点D，BE⊥AC于点E，交AD于点F，点Ｍ是BC的中点，连接FM并延长交AB的垂线BH于点H。下列说法中错误的是（ ）
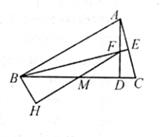A、若∠ABC=30°，则DF+BH= BD B、若∠ABC=45°，则DF+BH=BD C、若∠ABC=60°(点Ｍ与点D重合)，则DF+BH= BD D、若∠ABC=90°(点B与点D重合)，则DF+BH=BD7. 如图，以Rt△ABC各边为边分别向外作等边三角形，编号为①、②、③，将②、①如图所示依次叠在③上，已知四边形EMNC与四边形MPQN的面积分别为9 与7 ，则斜边BC的长为（ ）
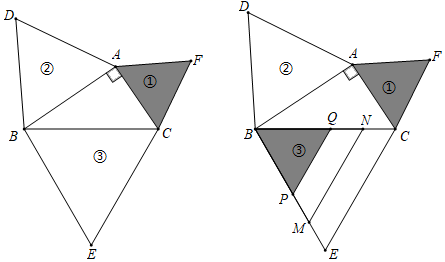A、5 B、9 C、10 D、168. 如图，在4×4的正方形网格中，每一格长度为1，小正方形的顶点称为格点，A，B，C，D，E，F都在格点上，以AB，CD，EF为边能构成一个直角三角形，则点F的位置有（ ）
A、1处 B、2处 C、3处 D、4处9. 如图，在△ABC中，∠ABC=90°，D为BC的中点，点E在AB上，AD，CE交于点F， AE=EF=4，FC=9，则cos∠ACB的值为（ ）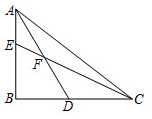
A、 B、 C、 D、10. 如图：四个形状大小相同的等腰三角形 ， ， ， 按如图摆放在正方形ABCD的内部，顺次连接E、F、G、H得到四边形EFGH.若 ，且EH = ，则BC的长为（ ）
A、 B、 C、 D、2二、填空题
-
11. 如图，AB＝AD，∠BAE＝∠DAC，要使△ABC≌△ADE，还需添加一个条件，这个条件可以是.
12. 如图，在锐角△ABC中，AB＝5 ，∠BAC＝45°，∠BAC的平分线交BC于点D，M，N分别是AD，AB上的动点，则BM+MN的最小值是 ．
13. 已知△ABC，按以下步骤作图：①分别以B，C为圆心，以大于 BC的长为半径作弧，两弧相交于两点M，N；②作直线MN交直线AB于点D，连接CD.若∠ABC＝40°，∠ACD＝30°，则∠BAC的度数为.14. 在平面直角坐标系中，点A（2，0），B（0，4），求点C，使以点B、O、C为顶点的三角形与△ABO全等，则点C的坐标为.15. 如图，∠AOB=30°，点M，N在边OA上，OM=x，ON=x+4，P是OB边上的一点，若使得△PMN为等腰三角形的点P只有1个，则x的取值范围是.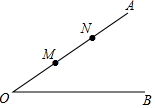
16. 两个大小不同的等腰直角三角板按如图方式摆放，使得A，B，P三点在同一直线上，连结 .若 ， ，则 的面积为.
17. 如图，在等边三角形ABC的AC，BC边上各取一点P，Q，使AP=CQ，AQ，BP相交于点O．若BO=6，PO=2，则AP的 ， AO的长为 ．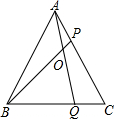
18. 如图，Rt△ACB中，∠ACB=90°，AC=2BC=4，点P为AB边中点，点D为AC边上不与端点重合的一动点，将△ADP沿着直线PD折叠得△PDE，若DE⊥AB，则AD的长度为。
三、综合题
-
19. 如图，△ABC中，∠C＝90°，AC＝3x﹣10.
(1)、已知AC＞2，求x的取值范围；(2)、若AB＝x+2，且x为整数，在（1）的条件下，求BC的长.20. △ABC和△DEF是两个全等的等腰直角三角形，∠BAC＝∠EDF＝90°，△EDF的顶点E与△ABC的斜边BC的中点重合，将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q.
(1)、如图①，当点Q在线段AC上，且AP＝AQ时，求证：△BPE≌△CQE；(2)、如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；(3)、在（2）的条件下，BP＝2，CQ＝9，则BC的长为.
21. 如图1，是小明荡秋千的侧面示意图，秋千链长AB＝5m（秋千踏板视作一个点），静止时秋千位于铅垂线BC上，此时秋千踏板A到地面的距离为0.5m.
(1)、当摆角为37°时，求秋千踏板A与地面的距离AH；（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）(2)、如图2，当秋千踏板摆动到点D时，点D到BC的距离DE＝4m；当他从D处摆动到D'处时，恰好D'B⊥DB，求点D'到BC的距离.22. 已知：如图，在Rt△ABC和Rt△ABD中，∠ACB＝90°，∠ABD＝90°，AB＝BD，BC＝4，（点A、D分别在直线BC的上下两侧），点G是Rt△ABD的重心，射线BG交边AD于点E，射线BC交边AD于点F.
(1)、求证：∠CAF＝∠CBE；(2)、当点F在边BC上，AC＝1时，求BF的长；(3)、若△BGC是以BG为腰的等腰三角形，试求AC的长.23. 如图，在正方形ABCD中，点E是对角线BD上任意一点，连接AE并延长AE交BC的延长线于点F，交CD于点G．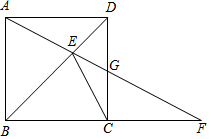
(1)、求证：∠DAE＝∠DCE；(2)、若∠F＝30°，DG＝2，求CG的长度．24. 如图1是一款“雷达式”懒人椅。当懒人椅完全展开时，其侧面示意图如图2所示，金属杆AB，CD在点O处连接，且分别与金属杆EF在点B，D处连接，金属杆CD的OD部分可以伸缩(即OD的长度可变)．已知0A=50cm，OB=20cm，OC=30cm，DE=BF=5cm．当把懒人椅完全叠合时，金属杆AB，CD，EF重合在一条直线上(如图3所示)，此时点E和点A重合。
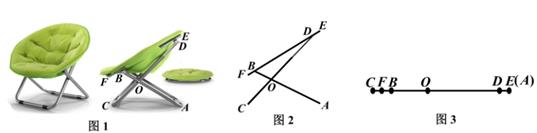(1)、如图2，已知∠BOD=6∠ODB，∠OBF=140°。①求∠AOC的度数。
②求点A，C之间的距离。
(2)、如图3，当懒人椅完全叠合时，求CF与CD的长。25. 如图，已知等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于点D，点P是BA延长线上一点，点O是线段AD上一点，OP=OC．
(1)、求∠APO+∠DCO的度数；(2)、求证：点P在OC的垂直平分线上．26. 如图1，在等边△ABC中，AB＝6cm，动点P从点A出发以1cm/s的速度沿AB匀速运动，动点Q同时从点C出发以同样的速度沿BC的延长线方向匀速运动，当点P到达点B时，点P、Q同时停止运动.设运动时间为t（s），过点P作PE⊥AC于E，PQ交AC边于D，线段BC的中点为M，连接PM.
(1)、当t为何值时，△CDQ与△MPQ相似；(2)、在点P、Q运动过程中，点D、E也随之运动，线段DE的长度是否会发生变化？若发生变化，请说明理由，若不发生变化，求DE的长；(3)、如图2，将△BPM沿直线PM翻折，得△B'PM，连接AB'，当t为何值时，AB'的值最小？并求出最小值.27. 如图，已知△ABC 是等腰直角三角形，动点 P 在斜边 AB 所在的直线上，以 PC 为直角边作等腰直角△PCQ，其中∠PCQ＝90°，探究并解决下列问题：
(1)、如图 1，若点 P为线段 AB 上一动点时，①求证：△ACP≌△BCQ；
②试求线段 PA，PB，PQ 三者之间的数量关系；
(2)、如图 2，若点 P 在 AB 的延长线上，求证：BQ⊥AP；(3)、若动点 P 满足 ，请直接写出 的值.28. 我们发现，“用不同的方式表示同一图形的面积”可以解决计算线段的有关问题，这种方法称为面积法.
(1)、如图1，在Rt△ABC中，∠ACB＝90°，AC＝3，BC＝4，CD是斜边AB边上的高线.用“面积法”求CD的长.(2)、如图2，在等腰三角形ABC中，AB＝AC＝13，BC＝10，P为底边BC上的任意一点，过点P作PM⊥AB，PN⊥AC，垂足分别为M，N，连结AP，利用S△ABC＝S△ABP+S△ACP ， 求PM+PN的值.(3)、如图3，有一直角三角形纸片ABE，∠ACE＝90°，AC＝4，EC＝6.点D在斜边AE上，连结CD，将△ADC沿CD折叠，点A的对应点A′落在EC边上，求折叠后纸片重叠部分的面积.