浙教版备考2021年中考数学三轮冲刺复习专题7 数与形规律
试卷更新日期:2021-05-16 类型:三轮冲刺
一、单选题
-
1. 求1+2+22+23+…+22020的值,可令S=1+2+22+23+…+22020 , 则2S=2+22+23+24+…+22021 , 因此2S-S=22021-1.仿照以上推理,计算出1+2020+20202+20203+…+20202020的值为( )A、 B、 C、 D、2. 我们把1,1,2,3,5,8,13,21,…这组数称为斐波那契数列,为了进一步研究,依次以这列数为半径作90°圆弧 , , ,…得到斐波那契螺旋线,然后顺次连结P1P2 , P2P3 , P3P4 , …得到螺旋折线(如图),已知点P1(0,1),P2(﹣1,0),P3(0,﹣1),则该折线上的点P9的坐标为( )
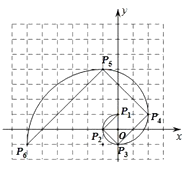 A、(﹣6,24) B、(﹣6,25) C、(﹣5,24) D、(﹣5,25)3. 一个正整数N的各位数字不全相等,且都不为0,现要将N的各位数字重新排列,可得到一个最大数和一个最小数,此最大数与最小数的和记为N的“和数”;此最大数与最小数的差记为N的“差数”。例如,245的“和数”为542+245=787;245的“差数”为542-245=297。一个四位数M,其中千位数字和百位数字均为a,十位数字为1,个位数字为b(且a≥1,b≥1),若它的“和数”是6666,则M的“差数”的值为( )A、3456或3996 B、4356或3996 C、3456或3699 D、4356或36994. 观察下面“品”字形中各数之间的规律,根据观察到的规律得出 的值为( )
A、(﹣6,24) B、(﹣6,25) C、(﹣5,24) D、(﹣5,25)3. 一个正整数N的各位数字不全相等,且都不为0,现要将N的各位数字重新排列,可得到一个最大数和一个最小数,此最大数与最小数的和记为N的“和数”;此最大数与最小数的差记为N的“差数”。例如,245的“和数”为542+245=787;245的“差数”为542-245=297。一个四位数M,其中千位数字和百位数字均为a,十位数字为1,个位数字为b(且a≥1,b≥1),若它的“和数”是6666,则M的“差数”的值为( )A、3456或3996 B、4356或3996 C、3456或3699 D、4356或36994. 观察下面“品”字形中各数之间的规律,根据观察到的规律得出 的值为( ) A、491 B、1045 C、1003 D、5335. 正方形ABCD的边长为1,其面积记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2 , …按此规律继续下去,则S2019的值为( )
A、491 B、1045 C、1003 D、5335. 正方形ABCD的边长为1,其面积记为S1 , 以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积记为S2 , …按此规律继续下去,则S2019的值为( )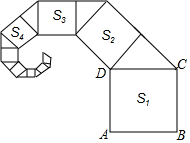 A、 B、 C、 D、6. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“
A、 B、 C、 D、6. 如图,在平面直角坐标系中,有若干个横纵坐标分别为整数的点,其顺序按图中“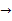 ”方向排序,如 , , ,…,根据这个规律,第 个点的横坐标为( )
”方向排序,如 , , ,…,根据这个规律,第 个点的横坐标为( )  A、44 B、45 C、46 D、477. 正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3 , …分别在直线y=x+1和x轴上,则点B6的坐标是( )
A、44 B、45 C、46 D、477. 正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , …按如图的方式放置.点A1 , A2 , A3 , …和点C1 , C2 , C3 , …分别在直线y=x+1和x轴上,则点B6的坐标是( ) A、(63,32) B、(64,32) C、(63,31) D、(64,31)8. 希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数.下列数中既是三角形数又是正方形数的是( )
A、(63,32) B、(64,32) C、(63,31) D、(64,31)8. 希腊人常用小石子在沙滩上摆成各种形状来研究数.例如:他们研究过图1中的1,3,6,10,…,由于这些数能够表示成三角形,将其称为三角形数;类似地,称图2中的1,4,9,16…这样的数成为正方形数.下列数中既是三角形数又是正方形数的是( )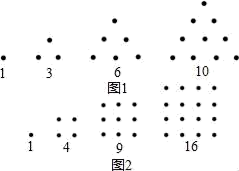 A、289 B、1024 C、1225 D、13789. 南宋数学家杨辉在其著作《解:九章算法》中揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将右表称为“杨辉三角”
A、289 B、1024 C、1225 D、13789. 南宋数学家杨辉在其著作《解:九章算法》中揭示了(a+b)n(n为非负整数)展开式的项数及各项系数的有关规律如下,后人也将右表称为“杨辉三角”(a+b)0=1
(a+b)1=a+b
(a+b)2=a2+2ab+b2
(a+b)3=a3+3a2b+3ab2+b3
(a+b)4=a4+4a3b+6a2b2+4ab3+b4
(a+b)5=a5+5a4b+10a3b2+10a2b3+5ab4+b5
…
则(a+b)9展开式中所有项的系数和是( )
 A、128 B、256 C、512 D、102410. 有这样一种算法,对于输入的任意一个实数,都进行“先乘以 ,再加3”的运算。现在输入一个x=4,通过第1次运算的结果为x1 , 再把x1输入进行第2次同样的运算,得到的运算结果为x2 , …,一直这样运算下去,当运算次数不断增加时,运算结果xn( )A、越来越接近4 B、越来越接近于-2 C、越来越接近2 D、不会越来越接近于一个固定的数
A、128 B、256 C、512 D、102410. 有这样一种算法,对于输入的任意一个实数,都进行“先乘以 ,再加3”的运算。现在输入一个x=4,通过第1次运算的结果为x1 , 再把x1输入进行第2次同样的运算,得到的运算结果为x2 , …,一直这样运算下去,当运算次数不断增加时,运算结果xn( )A、越来越接近4 B、越来越接近于-2 C、越来越接近2 D、不会越来越接近于一个固定的数二、填空题
-
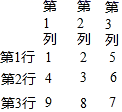
11. 把所有的正整数按一定规律排列成如图所示的数表,若根据行列分布,正整数6对应的位置记为(2,3),则位置(4,2)对应的正整数是.
 12. “天干地支”纪年法是中国古老的纪年法,由“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”十天干与“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”十二地支依次相配组成。如:甲子、乙丑、丙寅、10年后天干从“甲”重新开始纪年,12年后地支从“子”重新开始纪年,依次下去.公元2020年对应“庚子”年,下一次出现“庚子”年是公元年。13. 如图,小圆O的半径为1,△A1B1C1 , △A2B2C2 , △A3B3C3 , …,△AnBnCn依次为同心圆O的内接正三角形和外切正三角形,由弦A1C1和弧A1C1围成的弓形面积记为S1 , 由弦A2C2和弧A2C2围成的弓形面积记为S2 , …,由弦AnCn和弧AnCn围成的弓形面积记为Sn , 其中由弦A2020C2020和弧A2020C2020围成的弓形面积S2020为。
12. “天干地支”纪年法是中国古老的纪年法,由“甲、乙、丙、丁、戊、己、庚、辛、壬、癸”十天干与“子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥”十二地支依次相配组成。如:甲子、乙丑、丙寅、10年后天干从“甲”重新开始纪年,12年后地支从“子”重新开始纪年,依次下去.公元2020年对应“庚子”年,下一次出现“庚子”年是公元年。13. 如图,小圆O的半径为1,△A1B1C1 , △A2B2C2 , △A3B3C3 , …,△AnBnCn依次为同心圆O的内接正三角形和外切正三角形,由弦A1C1和弧A1C1围成的弓形面积记为S1 , 由弦A2C2和弧A2C2围成的弓形面积记为S2 , …,由弦AnCn和弧AnCn围成的弓形面积记为Sn , 其中由弦A2020C2020和弧A2020C2020围成的弓形面积S2020为。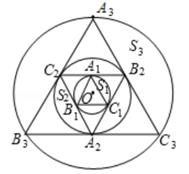 14. 设 ,(n为自然数),其中 与 分别表示 的整数部分和小数部分,如[2.5]=2, =0.5; , =0.4;则 =15. 如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆∁n的半径分别是r1、r2、r3…、rn , 则 =.
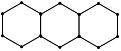
14. 设 ,(n为自然数),其中 与 分别表示 的整数部分和小数部分,如[2.5]=2, =0.5; , =0.4;则 =15. 如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆∁n的半径分别是r1、r2、r3…、rn , 则 =. 16. 如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍. 如果搭建正三角形和正六边形共用了2018根火柴棍,并且正三角形的个数比正六边形的个数多7个,那么能连续搭建正三角形的个数是;
16. 如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍. 如果搭建正三角形和正六边形共用了2018根火柴棍,并且正三角形的个数比正六边形的个数多7个,那么能连续搭建正三角形的个数是;

 17. 如图,在平面直角坐标系中,正方形OABC的边长为1,边OA,OC分别在x轴,y轴上,若以对角线OB为边作第二个正方形OBB1C1 , 再以对角线OB1为边作第三个正方形OB1B2C2 , 按此规律做下去,则 =
17. 如图,在平面直角坐标系中,正方形OABC的边长为1,边OA,OC分别在x轴,y轴上,若以对角线OB为边作第二个正方形OBB1C1 , 再以对角线OB1为边作第三个正方形OB1B2C2 , 按此规律做下去,则 = 18. 如图所示,一个机器人从O点出发,向正东方向走3m到达A1点,再向正北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,相对于点O,机器人走到A6时是位置.
18. 如图所示,一个机器人从O点出发,向正东方向走3m到达A1点,再向正北方向走6m到达A2点,再向正西方向走9m到达A3点,再向正南方向走12m到达A4点,再向正东方向走15m到达A5点,按如此规律走下去,相对于点O,机器人走到A6时是位置. 19. 一只电子跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后按图中箭头所示方向跳动,且每秒跳动一个单位,那么第2020秒时电子跳蚤所在位置的坐标是 。
19. 一只电子跳蚤在第一象限及x轴、y轴上跳动,在第一秒钟,它从原点跳动到(0,1),然后按图中箭头所示方向跳动,且每秒跳动一个单位,那么第2020秒时电子跳蚤所在位置的坐标是 。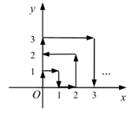 20. 在平面直角坐标系中,如果一个图形向右平移1个单位,再向上平移3个单位,称为一个变换,已知点A(1,-2),经过一个变换后对应点为A1 , 经过2个变换后对应点为A2 , …经过n个变换后对应点为An , 则用含n的代数式表示点An的坐标为。
20. 在平面直角坐标系中,如果一个图形向右平移1个单位,再向上平移3个单位,称为一个变换,已知点A(1,-2),经过一个变换后对应点为A1 , 经过2个变换后对应点为A2 , …经过n个变换后对应点为An , 则用含n的代数式表示点An的坐标为。三、综合题
-
21. 在多项式中有一类比较有趣的因式分解,如我们已经学过的(1)、证明: ;
(2)、据此猜想,对任意正整数 (不必证明);
(3)、利用(2),求 的值
22. (问题一):观察下列等式将以上三个等式两边分别相加得:
(1)、猜想并写出: .(2)、直接写出下列各式的计算结果:;
(3)、探究并计算:①.②
23. 如图,在△ABC中,沿∠BAC的平分线AB1折叠,剪掉重复部分;将余下部分沿∠B1A1C的平分线A1B2折叠,剪掉重复部分…将余下部分沿∠BnAnC的平分线AnBn+1折叠,点Bn与点C重合,无论折叠多少次,只要最后一次恰好重合,则称∠BAC是△ABC的好角.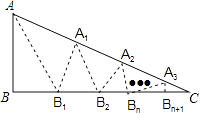 (1)、若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C (设∠B>∠C)之间的等量关系为 .
(1)、若经过n次折叠∠BAC是△ABC的好角,则∠B与∠C (设∠B>∠C)之间的等量关系为 .
(2)、若一个三角形的最小角是4°,且该三角形的三个角均是此三角形的好角.请写出符合要求三角形的另两个角的度数 . (写出一种即可)
24. 阅读材料:对于排好顺序的三个数: ,称为数列 .计算 的值,将这三个算式的最小值称为数列 的价值.例如,对于数列 ,因为 ,所以数列 的价值为 .
当改变数列中三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列 的价值为,数列 的价值等等.对于“ ”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为 .
根据以上材料,回答下列问题:
(1)、求数列 的价值;(2)、将“ ”这三个数按照不同的顺序排列,可得若干个数列,求取得的价值最小时的数列.(3)、已知 ,将“ ”这三个数按照不同的顺序排列,可得若干个数列,若这些数列的价值的最小值为1,求a的值.25. 如图,由两个长为2,宽为1的长方形组成“7”字图形。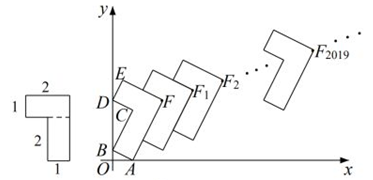 (1)、将一个“7”字图形按如图摆放在平面直角坐标系中,记为“7”字图形ABCDEF,其中顶点A位于x轴上,顶点B,D位于y轴上,O为坐标原点,则 的值为 .(2)、在(1)的基础上,继续摆放第二个“7”字图形得顶点F1 , 摆放第三个“7”字图形得顶点F2 , 依此类推,…,摆放第a个“7”字图形得顶点Fn-1 , …,则顶点F2019的坐标为 .26. 如图,在直角坐标系中,已知点M0的坐标为(1,0),将线段O M0绕原点O沿逆时针方向旋转45°,再将其延长到M1 , 使得M1 M0⊥O M0 , 得到线段OM1;又将线段OM1绕原点O沿逆时针方向旋转45°,再将其延长到M2 , 使得M2M1⊥OM1 , 得到线段OM2 , 如此下去,得到线段OM3 , OM4 , …,OMn
(1)、将一个“7”字图形按如图摆放在平面直角坐标系中,记为“7”字图形ABCDEF,其中顶点A位于x轴上,顶点B,D位于y轴上,O为坐标原点,则 的值为 .(2)、在(1)的基础上,继续摆放第二个“7”字图形得顶点F1 , 摆放第三个“7”字图形得顶点F2 , 依此类推,…,摆放第a个“7”字图形得顶点Fn-1 , …,则顶点F2019的坐标为 .26. 如图,在直角坐标系中,已知点M0的坐标为(1,0),将线段O M0绕原点O沿逆时针方向旋转45°,再将其延长到M1 , 使得M1 M0⊥O M0 , 得到线段OM1;又将线段OM1绕原点O沿逆时针方向旋转45°,再将其延长到M2 , 使得M2M1⊥OM1 , 得到线段OM2 , 如此下去,得到线段OM3 , OM4 , …,OMn (1)、写出点M5的坐标;(2)、求△M5OM6的周长;(3)、我们规定:把点Mn(xn , yn)(n=0,1,2,3…)的横坐标xn , 纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Mn的“绝对坐标”.根据图中点Mn的分布规律,请你猜想点Mn的“绝对坐标”,并写出来.27. 如图,一组抛物线的顶点A1(x1 , y1),A2(x2 , y2),…An(xn , yn)(n为正整数)依次是反比例函数 图象上的点,第一条抛物线以A1(x1 , y1)为顶点且过点O(0,0),B1(2,0),等腰△A1OB1为第一个三角形;第二条抛物线以A2(x2 , y2)为顶点且经过点B1(2,0),B2(4,0),等腰△A2B1B2为第二个三角形;…;第n条抛物线以An(xn , yn)为顶点且经过点Bn-1(2n-2,0),Bn(2n,0),等腰△AnBn-1Bn为第n个三角形.
(1)、写出点M5的坐标;(2)、求△M5OM6的周长;(3)、我们规定:把点Mn(xn , yn)(n=0,1,2,3…)的横坐标xn , 纵坐标yn都取绝对值后得到的新坐标(|xn|,|yn|)称之为点Mn的“绝对坐标”.根据图中点Mn的分布规律,请你猜想点Mn的“绝对坐标”,并写出来.27. 如图,一组抛物线的顶点A1(x1 , y1),A2(x2 , y2),…An(xn , yn)(n为正整数)依次是反比例函数 图象上的点,第一条抛物线以A1(x1 , y1)为顶点且过点O(0,0),B1(2,0),等腰△A1OB1为第一个三角形;第二条抛物线以A2(x2 , y2)为顶点且经过点B1(2,0),B2(4,0),等腰△A2B1B2为第二个三角形;…;第n条抛物线以An(xn , yn)为顶点且经过点Bn-1(2n-2,0),Bn(2n,0),等腰△AnBn-1Bn为第n个三角形. (1)、写出满足△AnBn-1Bn的面积为整数的n的值.(2)、若第n条抛物线为y=anx2+bnx+cn满足10an+5bn+cn=0,称“滑翔抛物线”,试求出满足条件的“滑翔抛物线”解析式为.
(1)、写出满足△AnBn-1Bn的面积为整数的n的值.(2)、若第n条抛物线为y=anx2+bnx+cn满足10an+5bn+cn=0,称“滑翔抛物线”,试求出满足条件的“滑翔抛物线”解析式为.