浙教版备考2021年中考数学三轮冲刺复习专题6 四边形
试卷更新日期:2021-05-16 类型:三轮冲刺
一、单选题
-
1. 如果一个正多边形内角和等于1080°,那么这个正多边形的每一个外角等于( )A、45° B、60° C、120° D、135°2. 如图,在平行四边形ABCD中,BD⊥AD,以BD为直径作圆,交于AB于E,交CD于F,若BD=12,AD:AB=1:2,则图中阴影部分的面积为( )
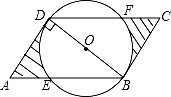 A、12 B、15 -6π C、30 ﹣12π D、 π3. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,矩形ABCD的边AB在x轴上,其中O点是坐标原点,AO=2,BO=3,BC=4,点A、B是固定点,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
A、12 B、15 -6π C、30 ﹣12π D、 π3. 我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,矩形ABCD的边AB在x轴上,其中O点是坐标原点,AO=2,BO=3,BC=4,点A、B是固定点,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为( )
 A、 B、 C、 D、4. 已知四边形ABCD是平行四边形,下列结论中不正确的是( )A、当AB=BC时,它是菱形 B、当AC=BD时,它是正方形 C、当AC⊥BD时,它是菱形 D、当∠ABC=90°时,它是矩形5. 如图,在菱形OABC中,AC=6,OB=8,点O为原点,点B在y轴正半轴上,若函数y= (k≠0)的图象经过点C,则k的值是( )
A、 B、 C、 D、4. 已知四边形ABCD是平行四边形,下列结论中不正确的是( )A、当AB=BC时,它是菱形 B、当AC=BD时,它是正方形 C、当AC⊥BD时,它是菱形 D、当∠ABC=90°时,它是矩形5. 如图,在菱形OABC中,AC=6,OB=8,点O为原点,点B在y轴正半轴上,若函数y= (k≠0)的图象经过点C,则k的值是( ) A、24 B、12 C、﹣12 D、﹣66. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC'D',若∠D'AB=30°,则菱形ABC'D'的面积与正方形ABCD的面积之比是( )
A、24 B、12 C、﹣12 D、﹣66. 四边形具有不稳定性,对于四条边长确定的四边形,当内角度数发生变化时,其形状也会随之改变.如图,改变正方形ABCD的内角,正方形ABCD变为菱形ABC'D',若∠D'AB=30°,则菱形ABC'D'的面积与正方形ABCD的面积之比是( )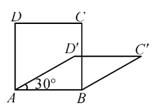 A、1 B、 C、 D、7. 如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( )
A、1 B、 C、 D、7. 如图,矩形ABCD中,AB=4,AD=2,E为AB的中点,F为EC上一动点,P为DF中点,连接PB,则PB的最小值是( ) A、2 B、4 C、 D、8. 如图,Rt△ACB中,∠C=90°,AC=6,BC=8,半径为1的⊙O与AC,BC相切,当⊙O沿边CB平移至与AB相切时,则⊙O平移的距离为( )
A、2 B、4 C、 D、8. 如图,Rt△ACB中,∠C=90°,AC=6,BC=8,半径为1的⊙O与AC,BC相切,当⊙O沿边CB平移至与AB相切时,则⊙O平移的距离为( )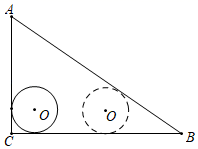 A、3 B、4 C、5 D、69. 如图,在平面直角坐标系中,一个含有45〫角的三角板的其中一个锐角顶点置于点A(﹣3,﹣3)处,将其绕点A旋转,这个45〫角的两边所在的直线分别交x轴,y轴的正半轴于点B,C,连结BC,函数y= (x>0)的图象经过BC的中点D,则( )
A、3 B、4 C、5 D、69. 如图,在平面直角坐标系中,一个含有45〫角的三角板的其中一个锐角顶点置于点A(﹣3,﹣3)处,将其绕点A旋转,这个45〫角的两边所在的直线分别交x轴,y轴的正半轴于点B,C,连结BC,函数y= (x>0)的图象经过BC的中点D,则( ) A、 B、 C、 D、10. 如图,在矩形ABCD中,点E,F将对角线AC三等分,已知 AB=9,BC=12,点P在矩形ABCD的边上,则满足PE+PF=12的点P的个数是( )
A、 B、 C、 D、10. 如图,在矩形ABCD中,点E,F将对角线AC三等分,已知 AB=9,BC=12,点P在矩形ABCD的边上,则满足PE+PF=12的点P的个数是( )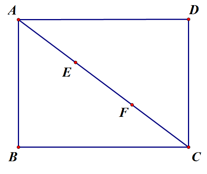 A、2 B、4 C、6 D、8
A、2 B、4 C、6 D、8二、填空题
-
11. 如图,▱ABCD的对角线AC、BD相交于点O,点E是AB的中点,△BEO的周长是8,则△BCD的周长为.
 12. 如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于F,则△AFC的面积为.
12. 如图,在△ABC中,∠BAC=90°,AB=4,AC=6,点D、E分别是BC、AD的中点,AF∥BC交CE的延长线于F,则△AFC的面积为.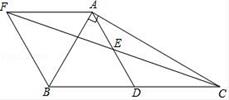 13. 如图,将边长为9的正方形纸片ABCD沿MN折叠,使点A落在BC边上 点处,点D的对应点为点 ,若 ,则DM=.
13. 如图,将边长为9的正方形纸片ABCD沿MN折叠,使点A落在BC边上 点处,点D的对应点为点 ,若 ,则DM=. 14. 已知E,F,G,H分别是四边形ABCD各边的中点,则当ACBD时,四边形EFGH是矩形.15. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交EG于点T,交FG于点P,则GT=.
14. 已知E,F,G,H分别是四边形ABCD各边的中点,则当ACBD时,四边形EFGH是矩形.15. 如图,边长分别为4和8的两个正方形ABCD和CEFG并排放在一起,连接BD并延长交EG于点T,交FG于点P,则GT=. 16. 在▱ABCD中,E是AD上一点,且点E将AD分为2:3的两部分,连接BE、AC相交于F,则S△AEF:S△CBF是.17. 如图2,小靓用边长为16的七巧板(如图1)拼成一幅装饰图,放入长方形ABCD内拼成一个“木马”形状(如图2),图中的三角形顶点E在边CD上,三角形的边AM、GF分别在边AD、BC上,则AB的长是.
16. 在▱ABCD中,E是AD上一点,且点E将AD分为2:3的两部分,连接BE、AC相交于F,则S△AEF:S△CBF是.17. 如图2,小靓用边长为16的七巧板(如图1)拼成一幅装饰图,放入长方形ABCD内拼成一个“木马”形状(如图2),图中的三角形顶点E在边CD上,三角形的边AM、GF分别在边AD、BC上,则AB的长是.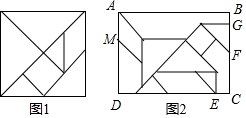 18. 如图,在矩形 中, 分别是 的中点, 分别在 , 上, 且 ,连结 ,则 与 重叠部分六边形 的周长为
18. 如图,在矩形 中, 分别是 的中点, 分别在 , 上, 且 ,连结 ,则 与 重叠部分六边形 的周长为
三、综合题
-
19. 如图,在平面直角坐标系xOy中,四边形OABC的顶点A在x轴的正半轴上,OA=4,OC=2,点D、E、F、G分别为边OA、AB、BC、CO的中点,连结DE、EF、FG、GD.

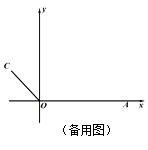 (1)、若点C在y轴的正半轴上,当点B的坐标为(2,4)时,判断四边形DEFG的形状,并说明理由.
(1)、若点C在y轴的正半轴上,当点B的坐标为(2,4)时,判断四边形DEFG的形状,并说明理由.
(2)、若点C在第二象限运动,且四边形DEFG为菱形时,求点四边形OABC对角线OB长度的取值范围.
(3)、若在点C的运动过程中,四边形DEFG始终为正方形,当点C从X轴负半轴经过Y轴正半轴,运动至X轴正半轴时,直接写出点B的运动路径长.
20. 已知:如图,四边形ABCD中,AD∥BC,对角线BD平分∠ABC,且BD⊥DC,E为BC中点,AB=DE.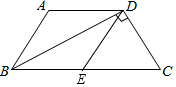 (1)、求证:四边形ABED是菱形;
(1)、求证:四边形ABED是菱形;
(2)、若∠C=60°,CD=4,求四边形ABCD的面积.
21. 如图1,若O是AB的中点,也是CD的中点,那么点称为AB与CD的结点。 (1)、如图2,已知四边形ABCD的对角线交于点O,且O是AC,BD的结点,请直接写出满足要求的四边形ABCD的名称(写出两个即可)(2)、如图3,在Rt△ABC中,∠C=90°,O是AB的中点,E是BC上一点,G是AC上一点,连结EG,过点G作EG的垂线,交EO的延长线于点∠EGC=∠GDA。求证:O是AB,DE的结点。(3)、在(2)的条件下,当BC=8,AC=6 ,且EG=DO时,求DG的长。22. 如图,正方形OABC的顶点O与原点重合,点A,C分别在x轴与y轴的正半轴上,点A的坐标为(4,0),点D在边AB上,且tan∠AOD= ,点E是射线OB上一动点,EF⊥x轴于点F,交射线OD于点G,过点G作GH∥x轴交AE于点H.
(1)、如图2,已知四边形ABCD的对角线交于点O,且O是AC,BD的结点,请直接写出满足要求的四边形ABCD的名称(写出两个即可)(2)、如图3,在Rt△ABC中,∠C=90°,O是AB的中点,E是BC上一点,G是AC上一点,连结EG,过点G作EG的垂线,交EO的延长线于点∠EGC=∠GDA。求证:O是AB,DE的结点。(3)、在(2)的条件下,当BC=8,AC=6 ,且EG=DO时,求DG的长。22. 如图,正方形OABC的顶点O与原点重合,点A,C分别在x轴与y轴的正半轴上,点A的坐标为(4,0),点D在边AB上,且tan∠AOD= ,点E是射线OB上一动点,EF⊥x轴于点F,交射线OD于点G,过点G作GH∥x轴交AE于点H. (1)、求B,D两点的坐标;(2)、当点E在线段OB上运动时,求∠HDA的大小;(3)、以点G为圆心,GH的长为半径画⊙G.是否存在点E使⊙G与正方形OABC的对角线所在的直线相切?若不存在,请说明理由;若存在,请求出所有符合条件的点E的坐标.23. 如图,矩形ABCD中,AB=6,BC=6 ,动点P从点A出发,以每秒 个单位长度的速度沿线段AD运动,动点Q从点D出发,以每秒2个单位长度的速度沿折线段D﹣O﹣C运动,已知P、Q同时开始移动,当动点P到达D点时,P、Q同时停止运动.设运动时间为t秒.
(1)、求B,D两点的坐标;(2)、当点E在线段OB上运动时,求∠HDA的大小;(3)、以点G为圆心,GH的长为半径画⊙G.是否存在点E使⊙G与正方形OABC的对角线所在的直线相切?若不存在,请说明理由;若存在,请求出所有符合条件的点E的坐标.23. 如图,矩形ABCD中,AB=6,BC=6 ,动点P从点A出发,以每秒 个单位长度的速度沿线段AD运动,动点Q从点D出发,以每秒2个单位长度的速度沿折线段D﹣O﹣C运动,已知P、Q同时开始移动,当动点P到达D点时,P、Q同时停止运动.设运动时间为t秒.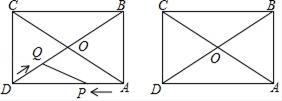 (1)、当t=1秒时,求动点P、Q之间的距离;(2)、若动点P、Q之间的距离为4个单位长度,求t的值;(3)、若线段PQ的中点为M,在整个运动过程中;直接写出点M运动路径的长度.24. 如图
(1)、当t=1秒时,求动点P、Q之间的距离;(2)、若动点P、Q之间的距离为4个单位长度,求t的值;(3)、若线段PQ的中点为M,在整个运动过程中;直接写出点M运动路径的长度.24. 如图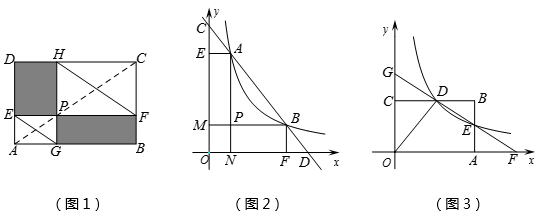 (1)、方法体验:
(1)、方法体验:如图1,点P在矩形ABCD的对角线AC上,且不与点A,C重合,过点P分别作边AB,AD的平行线,交两组对边于点E,F和G,H,容易证明四边形PEDH和四边形PFBG是面积相等的矩形,分别连结EG,FH.
①根据矩形PEDH和矩形PFBG面积相等的关系,那么PE·PH= ▲ .
②求证:EG∥FH.
(2)、方法迁移:如图2,已知直线 分别与x轴,y轴交于D,C两点,
与双曲线 交于A,B两点. 求证:AC=BD.
(3)、知识应用:如图3,反比例函数 (x>0)的图象与矩形ABCO的边BC交于点D,与边AB交于点E, 直线DE与x轴,y轴分别交于点F,G . 若矩形ABCO的面积为10,△ODG与△ODF的面积比为3:5,则k=.
25. 如图,在 中, , , .动点P以每秒5个单位长度的速度从点A出发,沿 的方向向终点C运动.点P关于点C的对称点为D,过点P作 于点Q,以 、 为边作 ,设点P的运动时间为 .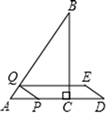 (1)、当点P在 上运动时,用含t的代数式表示 的长.(2)、当 为菱形时,求t的值.(3)、设 的面积为S,求S与t之间的函数关系式.(4)、作点E关于直线 的对称点 ,当点 落在 内部时,直接写出t的取值范围.26. 我们定义:连结凸四边形一组对边中点的线段叫做四边形的“准中位线”.
(1)、当点P在 上运动时,用含t的代数式表示 的长.(2)、当 为菱形时,求t的值.(3)、设 的面积为S,求S与t之间的函数关系式.(4)、作点E关于直线 的对称点 ,当点 落在 内部时,直接写出t的取值范围.26. 我们定义:连结凸四边形一组对边中点的线段叫做四边形的“准中位线”. (1)、概念理解:
(1)、概念理解:如图1,四边形ABCD中,F为CD的中点,∠ADB=90°,E是AB边上一点,满足DE=AE,试判断EF是否为四边形ABCD的准中位线,并说明理由。
(2)、问题探究:如图2,△ABC中,∠ACB=90°,AC=6,BC=8,动点E以每秒1个单位的速度,从点A出发向点C运动,动点F以每秒6个单位的速度,从点C出发沿射线CB运动,当点E运动至点C时,两点同时停止运动。D为线段AB上任意一点,连接并延长CD,射线CD与点A,B,E,F构成的四边形的两边分别相交于点M,N,设运动时间为t。问t为何值时,MN为点A,B,E,F构成的四边形的准中位线。
(3)、应用拓展:如图3,EF为四边形ABCD的准中位线,AB=CD,延长FE分别与BA,CD的延长线交于点M,N,请找出图中与∠M相等的角并证明。