浙教版备考2021年中考数学三轮冲刺复习专题5 探究性几何问题
试卷更新日期:2021-05-16 类型:三轮冲刺
一、单选题
-
1. 在如图所示的网格中,已知线段AB,现要在该网格内再确定格点C和格点D,某数学探究小组在探究时发现以下结论:以下结论错误的是( )
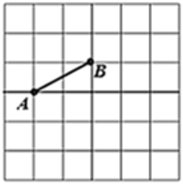 A、将线段 平移得到线段 ,使四边形 为正方形的有2种; B、将线段 平移得到线段 ,使四边形 为菱形的(正方形除外)有3种; C、将线段 平移得到线段 ,使四边形 为矩形的(正方形除外)有两种; D、不存在以 为对角线的四边形 是菱形.2. 如图,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究在第n个图中,黑、白瓷砖分别各有多少块( )
A、将线段 平移得到线段 ,使四边形 为正方形的有2种; B、将线段 平移得到线段 ,使四边形 为菱形的(正方形除外)有3种; C、将线段 平移得到线段 ,使四边形 为矩形的(正方形除外)有两种; D、不存在以 为对角线的四边形 是菱形.2. 如图,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下列图形,探究在第n个图中,黑、白瓷砖分别各有多少块( ) A、 , B、 , C、 , D、 ,3. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:
A、 , B、 , C、 , D、 ,3. 两组邻边分别相等的四边形叫做“筝形”,如图,四边形ABCD是一个筝形,其中AD=CD,AB=CB,在探究筝形的性质时,得到如下结论:①△ABD≌△CBD;②AC⊥BD;③四边形ABCD的面积= AC·BD.其中正确的结论有( )
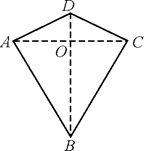 A、0个 B、1个 C、2个 D、3个4. 如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( )
A、0个 B、1个 C、2个 D、3个4. 如图,探究:用6个小正方形构造如图所示的网格图(每个小正方形的边长均为2),设经过图中M、P、H三点的圆弧与AH交于R,则弧HR的弧长为( )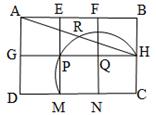 A、 B、 C、 D、5. 如图,某数学兴趣小组开展以下折纸活动:①对折矩形纸片ABCD , 使AD和BC重合,得到折痕EF , 把纸片展开;②再一次折叠纸片,使点A落在EF上,并使折痕经过点B , 得到折痕BM , 同时得到线段BN . 观察探究可以得到∠NBC的度数是( )
A、 B、 C、 D、5. 如图,某数学兴趣小组开展以下折纸活动:①对折矩形纸片ABCD , 使AD和BC重合,得到折痕EF , 把纸片展开;②再一次折叠纸片,使点A落在EF上,并使折痕经过点B , 得到折痕BM , 同时得到线段BN . 观察探究可以得到∠NBC的度数是( ) A、20° B、25° C、30° D、35°6. 在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( )
A、20° B、25° C、30° D、35°6. 在数学活动课上,老师出示两张等腰三角形纸片,如图所示.图1的三角形边长分别为4,4,2;图2的三角形的腰长也为4,底角等于图1中三角形的顶角;某学习小组将这两张纸片在同一平面内拼成如图3的四边形OABC,连结AC.该学习小组经探究得到以下四个结论,其中错误的是( )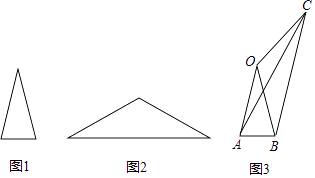 A、∠OCB=2∠ACB B、∠OAB+∠OAC=90° C、AC=2 D、BC=47. 如图, 的半径为2,圆心 在坐标原点,正方形 的边长为2,点 、 在第二象限,点 、 在 上,且点 的坐标为(0,2).现将正方形 绕点 按逆时针方向旋转150°,点 运动到了 上点 处,点 、 分别运动到了点 、 处,即得到正方形 (点 与 重合);再将正方形 绕点 按逆时针方向旋转150°,点 运动到了 上点 处,点 、 分别运动到了点 、 处,即得到正方形 (点 与 重合),……,按上述方法旋转2020次后,点 的坐标为( )
A、∠OCB=2∠ACB B、∠OAB+∠OAC=90° C、AC=2 D、BC=47. 如图, 的半径为2,圆心 在坐标原点,正方形 的边长为2,点 、 在第二象限,点 、 在 上,且点 的坐标为(0,2).现将正方形 绕点 按逆时针方向旋转150°,点 运动到了 上点 处,点 、 分别运动到了点 、 处,即得到正方形 (点 与 重合);再将正方形 绕点 按逆时针方向旋转150°,点 运动到了 上点 处,点 、 分别运动到了点 、 处,即得到正方形 (点 与 重合),……,按上述方法旋转2020次后,点 的坐标为( )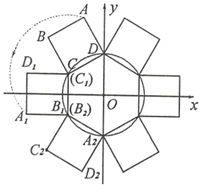 A、(0,2) B、 C、 D、8. 有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形,如图①,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了图②,如果继续“生长”下去 ,它将变得“枝繁叶茂”,则“生长”了2 014次后形成的图形中所有正方形的面积和是( )
A、(0,2) B、 C、 D、8. 有一个面积为1的正方形,经过一次“生长”后,在它的左右肩上生出两个小正方形,如图①,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了图②,如果继续“生长”下去 ,它将变得“枝繁叶茂”,则“生长”了2 014次后形成的图形中所有正方形的面积和是( ) A、2 012 B、2 013 C、2 014 D、2 0159. 如图甲,直角三角形 的三边a,b,c,满足 的关系.利用这个关系,探究下面的问题:如图乙, 是腰长为1的等腰直角三角形, ,延长 至 ,使 ,以 为底,在 外侧作等腰直角三角形 ,再延长 至 ,使 ,以 为底,在 外侧作等腰直角三角形 ,……,按此规律作等腰直角三角形 ( ,n为正整数),则 的长及 的面积分别是( )
A、2 012 B、2 013 C、2 014 D、2 0159. 如图甲,直角三角形 的三边a,b,c,满足 的关系.利用这个关系,探究下面的问题:如图乙, 是腰长为1的等腰直角三角形, ,延长 至 ,使 ,以 为底,在 外侧作等腰直角三角形 ,再延长 至 ,使 ,以 为底,在 外侧作等腰直角三角形 ,……,按此规律作等腰直角三角形 ( ,n为正整数),则 的长及 的面积分别是( )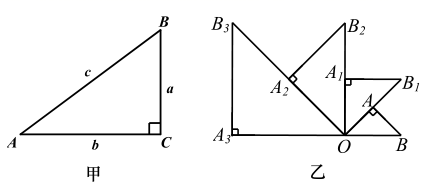 A、2, B、4, C、 , D、2,10. 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示:按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转……连续经过六次旋转.在旋转的过程中,当正方形和正六边形的边重合时,点B,M间的距离可能是( )
A、2, B、4, C、 , D、2,10. 已知正方形MNOK和正六边形ABCDEF边长均为1,把正方形放在正六边形中,使OK边与AB边重合,如图所示:按下列步骤操作:将正方形在正六边形中绕点B顺时针旋转,使KM边与BC边重合,完成第一次旋转;再绕点C顺时针旋转,使MN边与CD边重合,完成第二次旋转……连续经过六次旋转.在旋转的过程中,当正方形和正六边形的边重合时,点B,M间的距离可能是( ) A、0.5 B、0.7 C、 ﹣1 D、 ﹣1
A、0.5 B、0.7 C、 ﹣1 D、 ﹣1二、填空题
-
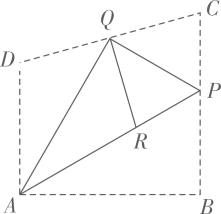
11. 在数学探究活动中,敏敏进行了如下操作:如图,将四边形纸片 沿过点A的直线折叠,使得点B落在 上的点 处,折痕为 ;再将 分别沿 折叠,此时点 落在 上的同一点R处.请完成下列探究:
 (1)、 的大小为 ;(2)、当四边形 是平行四边形时 的值为 .12. “皮克定理”是用来计算顶点在格点(即图中虚线的交点,如图中的小黑点)上的多边形的面积公式,公式为S = a + -1.小明只记得公式中的表示多边形的面积,a 和 b 中有一个表示多边形边上(含多边形顶点)的格点个数,另一个表示多边形内部的格点个数,但记不清楚究竟是哪一个表示多边形内部的格点个数,请你利用图 1 探究并运用探究的结果求图 2 中多边形的面积是.
(1)、 的大小为 ;(2)、当四边形 是平行四边形时 的值为 .12. “皮克定理”是用来计算顶点在格点(即图中虚线的交点,如图中的小黑点)上的多边形的面积公式,公式为S = a + -1.小明只记得公式中的表示多边形的面积,a 和 b 中有一个表示多边形边上(含多边形顶点)的格点个数,另一个表示多边形内部的格点个数,但记不清楚究竟是哪一个表示多边形内部的格点个数,请你利用图 1 探究并运用探究的结果求图 2 中多边形的面积是.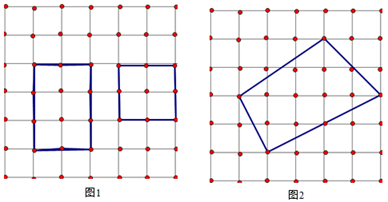 13. 观察下面图形,按要求找角(不含平角),如图①,两条直线交于同一点O,共有对对顶角;如图②,三条直线交于同一点O,共有对对顶角;探究:若有 条直线相交于同一点,则可形成对对顶角.
13. 观察下面图形,按要求找角(不含平角),如图①,两条直线交于同一点O,共有对对顶角;如图②,三条直线交于同一点O,共有对对顶角;探究:若有 条直线相交于同一点,则可形成对对顶角. 14. 如图,在平面直角坐标系xOy中,已知抛物线 y=-x(x-3)(0≤x≤3) 在x轴上方部分记作C1 , 它与x轴交于点O,A1 , 将C1绕点A1旋转180°得C2 , C2与x 轴交于另一点A2 . 继续操作并探究:将C2绕点A2旋转180°得C3 , 与x 轴交于另一点A3;将C3绕点A 2旋转180°得C4 , 与x 轴交于另一点A4 , 这样依次得到x轴上的点A1 , A2 , A3 , …,An , …,及抛物线C1 , C2 , …,Cn , ….则点A4的坐标为;Cn的顶点坐标为(n为正整数,用含n的代数式表示) .
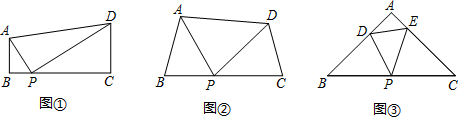
14. 如图,在平面直角坐标系xOy中,已知抛物线 y=-x(x-3)(0≤x≤3) 在x轴上方部分记作C1 , 它与x轴交于点O,A1 , 将C1绕点A1旋转180°得C2 , C2与x 轴交于另一点A2 . 继续操作并探究:将C2绕点A2旋转180°得C3 , 与x 轴交于另一点A3;将C3绕点A 2旋转180°得C4 , 与x 轴交于另一点A4 , 这样依次得到x轴上的点A1 , A2 , A3 , …,An , …,及抛物线C1 , C2 , …,Cn , ….则点A4的坐标为;Cn的顶点坐标为(n为正整数,用含n的代数式表示) .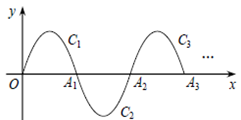 15. 感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)
15. 感知:如图①,在四边形ABCD中,AB∥CD,∠B=90°,点P在BC边上,当∠APD=90°时,可知△ABP∽△PCD.(不要求证明)探究:如图②,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时,求证:△ABP∽△PCD.
拓展:如图③,在△ABC中,点P是边BC的中点,点D、E分别在边AB、AC上.若∠B=∠C=∠DPE=45°,BC=6 ,CE=4,则DE的长为.
三、综合题
-
16. 数轴是一个非常重要的数学工具,它使数和数轴上的点建立起对应关系,揭示了数与点之间的内在联系,它是“数形结合”的基础.小白在草稿纸上画了一条数轴进行操作探究:
 (1)、操作一:折叠纸面,若使表示的点1与﹣1表示的点重合,则﹣2表示的点与表示的点重合;(2)、操作二:折叠纸面,若使1表示的点与﹣3表示的点重合,回答以下问题:
(1)、操作一:折叠纸面,若使表示的点1与﹣1表示的点重合,则﹣2表示的点与表示的点重合;(2)、操作二:折叠纸面,若使1表示的点与﹣3表示的点重合,回答以下问题:① 表示的点与数表示的点重合;
②若数轴上A、B两点之间距离为8(A在B的左侧),且A、B两点经折叠后重合,则A、B两点表示的数分别是;
(3)、操作三:在数轴上剪下9个单位长度(从﹣1到8)的一条线段,并把这条线段沿某点折叠,然后在重叠部分某处剪一刀得到三条线段(如图). 若这三条线段的长度之比为1:1:2,则折痕处对应的点所表示的数可能是.17. 【问题提出】如何把n个边长为1的正方形,剪拼成一个大正方形?(1)、【解决方法】探究一:若n是完全平方数,我们不用剪切小正方形,可直接将小正方形拼成一个大正方形,如图(1),用四个边长为1的小正方形可以拼成一个大正方形.问题1:请用9个边长为1的小正方形在图(2)的位置拼成一个大正方形.
 (2)、【解决方法】探究二:若n=2,5,10,13等这些数,都可以用两个正整数的平方和来表示,以n=5为例,用5个边长为1的小正方形剪拼成一个大正方形.
(2)、【解决方法】探究二:若n=2,5,10,13等这些数,都可以用两个正整数的平方和来表示,以n=5为例,用5个边长为1的小正方形剪拼成一个大正方形.计算:拼成的大正方形的面积为5,边长为 ,可表示成 ;
剪切:如图(3)将5个小正方形按如图所示分成5部分,虚线为剪切线;
拼图:以图(3)中的虚线为边,拼成一个边长为 的大正方形,如图(4).

问题2:请仿照上面的研究方式,用13个边长为1的小正方形剪拼成一个大正方形;
①计算:拼成的大正方形的面积为 , 边长为 , 可表示成;
②剪切:请仿照图(3)的方法,在图(5)的位置画出图形.
③拼图:请仿照图(4)的方法,在图(6)的位置出拼成的图.
18. 问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E,F分别是BC,CD上的点,且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.
小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是什么;

探索延伸:
如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°,E,F分别是BC,CD上的点,且∠EAF= ∠BAD,上述结论是否仍然成立,并说明理由;
实际应用:
如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进,1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.
19. 探究与发现:(1)、(探究一)我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?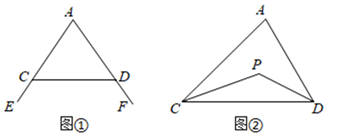
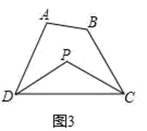
已知:如图①,∠FDC与∠ECD分别为 ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系,并证明你探究的数量关系.
(2)、(探究二)三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?已知:如图②,在 ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠A与∠P的数量关系,并证明你探究的数量关系.
(3)、(探究三)若将 ADC改成任意四边形ABCD呢?已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论直接写出∠A+∠B与∠P的数量关系 .
20. 探究等边三角形“手拉手”问题. (1)、如图1,已如△ABC , △ADE均为等边三角形,点D在线段BC上,且不与点B、点C重合,连接CE , 试判断CE与BA的位置关系,并说明理由;(2)、如图2,已知△ABC、△ADE均为等边三角形,连接CE、BD , 若∠DEC=60°,则∠ADB+∠ADE=度;(3)、如图3,已知点E在等边三角形△ABC外,点E、点B位于线段AC的异侧,连接BE、CE . 若∠BEC=60°,猜想线段BE、AE、CE三者之间的数量关系,并说明理由.21. 综合与探究
(1)、如图1,已如△ABC , △ADE均为等边三角形,点D在线段BC上,且不与点B、点C重合,连接CE , 试判断CE与BA的位置关系,并说明理由;(2)、如图2,已知△ABC、△ADE均为等边三角形,连接CE、BD , 若∠DEC=60°,则∠ADB+∠ADE=度;(3)、如图3,已知点E在等边三角形△ABC外,点E、点B位于线段AC的异侧,连接BE、CE . 若∠BEC=60°,猜想线段BE、AE、CE三者之间的数量关系,并说明理由.21. 综合与探究
【问题】如图1,在Rt△ABC中,∠ACB=90°,AC=BC,过点C作直线l平行于AB,∠EDF=90,点D在直线l上移动,角的一边DE始终经过点B,另一边DF与AC交于点P,研究DP和DB的数量关系。
【探究发现】
(1)、如图2,某数学学习小组运用“从特殊到一般”的数学思想,发现当点D移动到使点P与点C重合时,很容易就可以得到DP=DB,请写出证明过程;(2)、如图3,若点P是AC上的任意一点(不含端点A、C),受(1)的启发,另一个学习小组过点D作DG⊥CD交BC于点G,就可以证明DP=DB,请完成证明过程。(3)、若点P是CA延长线上的任意一点,在图(4)中补充完整图形,并判断结论是否仍然成立。22. 已知线段 ,点M是线段 上一动点,以 为直径作 ,点C是圆周上一点且 ,连接 ,过点A做直线 的垂线,交 于点N , 连接 ,设线段 的长为 ,线段 的长为 ,线段 的长为 .
小华同学根据学习函数的经验,分别对函数 ,随自变量x的变化而变化的规律进行了探究.
下面是该同学的探究过程,请补充完整:
(1)、按照下表中自变量x的值进行取点、画图、测量,分别得到了 与x的几组对应值:0
1
2
3
4
5
6
4.47
5.24
5.86
5.96
4.72
4.00
6.00
5.86
5.23
3.98
2.46
1.06
0
请你补全表格的相关数值,保留两位小数.
(2)、在同一平面直角坐标系 中,描出补全后的表中各组数值所对应的点 , ,并画出函数 的图象(函数 的图象如图,请你画出 的图象) (3)、结合画出的函数图象,解决问题:当 是等腰三角形时, 的长度约为 .23. 我们学过正多边形及其性质,了解了正多边形各边相等、各内角相等、具有轴对称性和旋转不变性……,下面我们继续探究正五边形相关线段及角的关系:
(3)、结合画出的函数图象,解决问题:当 是等腰三角形时, 的长度约为 .23. 我们学过正多边形及其性质,了解了正多边形各边相等、各内角相等、具有轴对称性和旋转不变性……,下面我们继续探究正五边形相关线段及角的关系:如图1,正五边形ABCDE中,
 (1)、连接AC,并作AF⊥CD,则∠CAF=度;(2)、连接BE,交AC于点G,求证:四边形GCDE是菱形;(3)、如图2,是一个斜网格图(8×8),每个小菱形的较小内角是72°,请利用一把角尺(只能画直角和直线,不能度量,可以用三角板替代)在网格图中画出以AB为一边的正五边形ABCDE(保留作图痕迹)。
(1)、连接AC,并作AF⊥CD,则∠CAF=度;(2)、连接BE,交AC于点G,求证:四边形GCDE是菱形;(3)、如图2,是一个斜网格图(8×8),每个小菱形的较小内角是72°,请利用一把角尺(只能画直角和直线,不能度量,可以用三角板替代)在网格图中画出以AB为一边的正五边形ABCDE(保留作图痕迹)。 24. 问题探究
24. 问题探究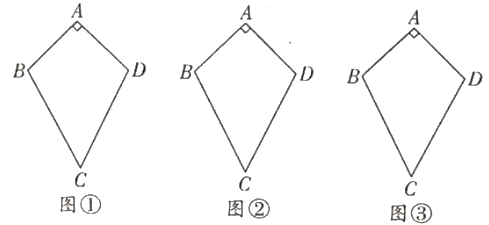
如图①②,在四边形ABCD中,AB=AD,CB=CD,∠A=90°;
(1)、在图①中作一条直线将四边形ABCD的面积二等分;
(2)、已知AB=2,BC= ,在图②四边形ABCD内部求作一点P,使得PB=PD,且折线B-P-D将四边形ABCD面积二等分;并求折线段B-P-D的长度;
(3)、问题解决:如图③,植物园有一块空地ABCD,其中AB=AD=100m,CB=CD=100 m,∠A=90°.根据视觉效果和花期特点,植物园设计部门想在这块空地上种上等面积的两种不同的花,要求从入口B修一条笔直的小路将这块地的面积二等分(小路面积忽略不计),以方便游客观赏,请通过计算,画图说明设计部门能否实现,若能实现,求出小路的长度;若不能,说明理由.25. 某数学活动小组在一次活动中,对一个数学问题作如下探究:
 (1)、(问题发现)如图1,AD,BD为⊙O的两条弦(AD<BD),点C为 的中点,过C作CE⊥BD,垂足为E.求证:BE=DE+AD.
(1)、(问题发现)如图1,AD,BD为⊙O的两条弦(AD<BD),点C为 的中点,过C作CE⊥BD,垂足为E.求证:BE=DE+AD.(问题探究)小明同学的思路是:如图2,在BE上截取BF=AD,连接CA,CB,CD,CF.……请你按照小明的思路完成上述问题的证明过程.
(2)、(结论运用)如图3,△ABC是⊙O的内接等边三角形,点D是 上一点,∠ACD=45°,连接BD,CD,过点A作AE⊥CD,垂足为E.若AB= ,则△BCD的周长为.(3)、(变式探究)如图4,若将(问题发现)中“点C为 的中点”改为“点C为优弧 的中点”,其他条件不变,上述结论“BE=DE+AD”还成立吗?若成立,请说明理由;若不成立,请写出BE、AD、DE之间的新等量关系,并加以证明.26. 探究函数 的图象与性质.小娜根据学习函数的经验,对函数 的图象与性质进行了探究.下面是小娜的探究过程,请补充完整:
(1)、下表是x与y的几组对应值.x
…
-2
-1
0
1
2
3
…
y
…
-8
-3
0
m
n
1
3
…
请直接写出:m= , n=;
(2)、如图,小娜在平面直角坐标系xOy中,描出了上表中已经给出的各组对应值为坐标的点,请再描出剩下的两个点,并画出该函数的图象;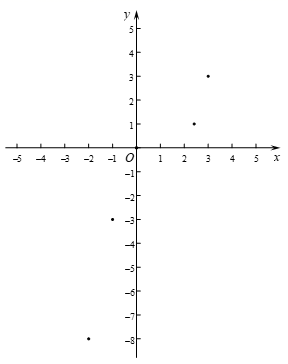 (3)、结合画出的函数图象,解决问题:若方程 有三个不同的解,记为x1 , x2 , x3 , 且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.27.(1)、问题提出
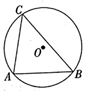
(3)、结合画出的函数图象,解决问题:若方程 有三个不同的解,记为x1 , x2 , x3 , 且x1< x2<x3. 请直接写出x1+ x2+x3的取值范围.27.(1)、问题提出如图, 是 的弦,点 是 上的一点,在直线 上方找一点 ,使得 ,画出 ,并说明理由;
 (2)、问题探究
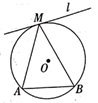
(2)、问题探究如图, 是 的弦,直线 与 相切于点 ,点 ,是直线 上异于点 的任意一点,请在图中画出图形,试判断 的大小关系;并说明理由;
 (3)、问题解决
(3)、问题解决如图,有一个平面图为五边形ABCDE的展览馆,其中 , , .展览馆保卫人员想在线段 上选一点 安装监控装置,用来监视边 ,现只要使 最大,就可以让监控装置的效果达到最佳,问在线段 上是否存在点 ,使 最大?若存在,请求出符合条件的 的长,若不存在,请说明理由.
 28.(1)、发现问题:
28.(1)、发现问题:如图1,AB为⊙O的直径,请在⊙O上求作一点P,使∠ABP=45°.(不必写作法)
 (2)、问题探究:
(2)、问题探究:如图2,等腰直角三角形△ABC中,∠A=90°,AB=AC=3 ,D是AB上一点,AD=2 ,在BC边上是否存在点P,使∠APD=45°?若存在,求出BP的长度,若不存在,请说明理由.
(3)、问题解决:如图3,为矩形足球场的示意图,其中宽AB=66米、球门EF=8米,且EB=FA.点P、Q分别为BC、AD上的点,BP=7米,∠BPQ=135,一位左前锋球员从点P处带球,沿PQ方向跑动,球员在PQ上的何处才能使射门角度(∠EMF)最大?求出此时PM的长度.