浙教版备考2021年中考数学三轮冲刺复习专题4 统计与概率
试卷更新日期：2021-05-16 类型：三轮冲刺
一、单选题
-
1. 下列调查方式，你认为最合适的是（ ）。A、要调查一批灯管的使用寿命，采全面调查的方式 B、杭州机场对旅客进行登机前安检，采用抽样调查方式 C、为了调查2019年度浙江省人均收入情况，调查省会城市杭州的人均收入 D、为了解台州市市民疫情期间的物资采购情况，采取抽样调查方式2. 下列事件中是必然事件的有（ ）A、抛掷一枚质地均匀的硬币，着地时正面向上 B、三角形内心到三边距离相等 C、测量宁波某天的最低气温，结果为 D、某个数的绝对值大于03. 在学校的体育训练中，小杰投实心球的7次成绩就如统计图所示，则这7次成绩的中位数和众数分别是（ ）
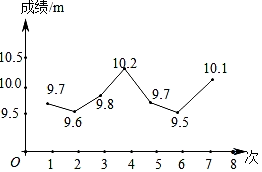A、9.7m，9.8m B、9.7m，9.7m C、9.8m，9.9m D、9.8m，9.8m4. 某班有40人，一次体能测试后，老师对测试成绩进行了统计.由于小亮没有参加本次集体测试因此计算其他39人的平均分为90分，方差s2＝41.后来小亮进行了补测，成绩为90分，关于该班40人的测试成绩，下列说法正确的是（ ）A、平均分不变，方差变大 B、平均分不变，方差变小 C、平均分和方差都不变 D、平均分和方差都改变5. 一组数据1，1，1，3，5，9，17，若加入一个整数a，一定不会发生变化的统计量是（ ）A、平均数 B、中位数 C、方差 D、众数6. 乐乐把报纸上看到甲、乙两公司2013年 年的销售收入情况如图所示：
关于两家公司 年的销售收入的增长速度，下列说法正确的是（ ）
A、甲快 B、乙快 C、一样快 D、无法比较7. 一次数学测试，某小组5名同学的成绩统计如下(有两个数据被遮盖)：组员
甲
乙
丙
丁
戊
平均成绩
众数
得分
81
77
■
80
82
80
●
则被遮盖的两个数据依次是（ ）
A、80，80 B、81，80 C、80，2 D、81，28. 疫情无情，人间有爱，为全力支援武汉开展新型冠状病毒感染肺炎医疗救治工作，打赢疫情防控战，温岭市某学校数学组25名老师积极捐款，捐款情况如下表所示，下列说法错误的是（ ）捐款数额(单位：元)
100
200
300
500
1000
人数(单位：人)
2
12
8
2
1
A、众数是200 B、中位数是300 C、极差是900 D、平均数是2809. 某学习小组做“用频率估计概率”的实验时，统计了某一结果出现的频率，绘制了如表的表格，则符合这一结果的实验最有可能的是（ ）实验次数
100
200
300
500
800
1000
2000
频率
0.365
0.328
0.330
0.334
0.336
0.332
0.333
A、抛一枚硬币，出现正面 B、一副去掉大小王的普通扑克牌洗匀后，从中任抽一张牌的花色是红桃 C、抛一个质地均匀的正六面体骰子（六个面上分别标有1，2，3，4，5，6），向上的面点数是5 D、从一个装有2个白球和1个红球的袋子中任取一球，取到红球10. 在一只不透明的口袋中放入红球5个，黑球1个，黄球n个，这些球除颜色不同外，其它无任何差别.搅匀后随机从中摸出一个恰好是黄球的概率为 ，则放入口袋中的黄球总数n是（ ）A、3 B、4 C、5 D、6二、填空题
-
11. 某校在全校学生中举办了一次“交通安全知识”测试，张老师从全校学生的答卷中随机地抽取了部分学生的答卷，将测试成绩按“差”、“中”、“良”、“优”划分为四个等级，并绘制成如图所示的条形统计图.若该校学生共有2000人，则其中成绩为“良”和“优”的总人数估计为人.
12. 已知3，a，4，b，5这五个数据，其中a，b是方程x2﹣3x+2＝0的两个根，则这五个数据的标准差是 ．13. 已知一组数据 的平均数是3，则数据 的平均数是14. 从正三角形、正方形、正五边形、圆这四个图形中随机选出一个图形，结果是中心对称图形的概率为.15. 如图是九（1）班45名同学每周课外阅读时间的频数直方图（每组含前一个边界值，不含后一个边界值）.其中每周课外阅读时间在6小时及以上的人有名.
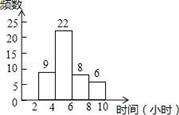16. 某公司欲招聘一名公关人员，对甲、乙两位候选人进行了面试和笔试，他们的成绩如表：候选人
甲
乙
测试成绩(百分制)
面试
86
92
笔试
90
83
如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权。根据两人的平均成绩，公司将录取.
17. 如图，现将方格内空白的小正方形（A，B，C，D，E，F）中任取2个涂黑，得到新图案.请用列表或画树状图的方法求新图案是轴对称图形的概率是.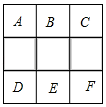
18. 小明和小红玩抛硬币游戏，连续抛两次，小明说：“如果两次都是正面，那么你赢；如果两次是一正一反，则我赢.”小红赢的概率是 ， 据此判断该游戏（填“公平”或“不公平”）.三、综合题
-
19. 一个不透明的布袋里装有2个红球，1个白球，它们除颜色外其余都相同.(1)、摸出1个球，记下颜色后不放回，再摸出1个球，求两次摸出的球恰好颜色相同的概率（要求画树状图或列表）.(2)、现再将 个白球放入布袋，搅匀后，使摸出1个球是白球的概率为 ，求 的值.20. 某校组织全校1200名学生进行经典诗词诵读活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取40名学生调查“一周诗词诵背数量”，根据调查结果绘制成的统计图如图所示.
大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表如下：
一周诗词诵背数量
3首
4首
5首
6首
7首
8首
人数
1
3
5
6
10
15
请根据调查的信息分析：
(1)、估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数.(2)、选择适当的统计量，至少从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果.21. 甲乙两人依次测量同一圆柱体工件的横截面直径(单位：cm)，测得的数据分别如表1、表2。表1：甲的测量数据
测量数据
9.8
9.9
10
10.1
10.3
频数
1
3
3
2
1
表2：乙的测量数据
测量数据
9.7
9.8
10
10.1
10.3
频数
1
2
3
2
2
(1)、如果在这些测量数据中选择一个数据作为工件直径的估计值，应该是那个数据？请说明理由。(2)、如果甲再测量一次，求他测量出的数据恰好是估计值的概率。(3)、请直接判断甲乙两人谁的测量技术更好(填甲或乙)，你选择的统计量是 。22. 某高中学校为使高一新生入校后及时穿上合身的校服，现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查，并根据调查结果绘制了如图两个不完整的统计图（校服型号以身高作为标准，共分为6种型号）．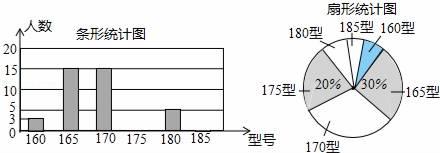
根据以上信息，解答下列问题：
(1)、该班共有多少名学生？其中穿175型校服的学生有多少？(2)、在条形统计图中，请把空缺部分补充完整．(3)、在扇形统计图中，请计算185型校服所对应的扇形圆心角的大小；(4)、求该班学生所穿校服型号的众数和中位数．23. 某校九年级为了解学生课堂发言情况，随机抽取该年级部分学生，对他们某天在课堂上发言的次数进行了统计，其结果如表，并绘制了如图所示的两幅不完整的统计图，已知B、E两组发言人数的比为5：2，请结合图中相关数据回答下列问题：发言次数n
A
0≤n＜3
B
3≤n＜6
C
6≤n＜9
D
9≤n＜12
E
12≤n＜15
F
15≤n＜18
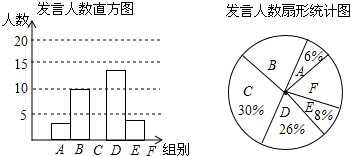(1)、求样本容量，并补全直方图；(2)、该年级共有学生500人，请估计全年级在这天里发言次数不少于12的次数；(3)、已知A组发言的学生中恰有1位女生，E组发言的学生中有2位男生，现从A组与E组中分别抽一位学生写报告，请用列表法或画树状图的方法，求所抽的两位学生恰好是一男一女的概率.24. 为做好全国文明城市的创建工作，我市交警连续10天对某路口100个“50岁以下行人”和100个“50岁及以上行人”中出现交通违章的情况进行了调查统计，将所得数据绘制成如下统计图.请根据所给信息，解答下列问题
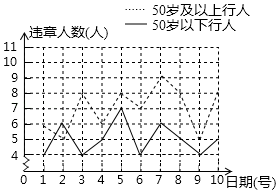(1)、求这10天“50岁及以上行人”中每天违章人数的众数；(2)、某天中午下班时段经过这一路口的“50岁以下行人”为300人，请估计大约有多少人会出现交通违章行为；(3)、请选择适当的统计量分析“50岁以下行人”和“50岁以上行人”交通违章行为的现并就“文明城市创建减少交通违章”提出合理建议.25. 为了了解学生关注热点新闻的情况，“两会”期间，小明对班级同学一周内收看“两会”新闻的次数情况作了调查，调查结果统计如图所示（其中男生收看3次的人数没有标出）根据上述信息，解答下列各题：
(1)、该班级女生人数是.女生收看“两会”新闻次数的中位数是.(2)、对于某个群体，我们把一周内收看某热点新闻次数不低于3次的人数占其所在群体总人数的百分比叫做该群体对某热点新闻的“关注指数”如果该班级男生对“两会”新闻的“关注指数”比女生低5％，试求该班级男生人数；(3)、为进一步分析该班级男、女生收看“两会”新闻次数的特点，小明给出了男生的部分统计统计量
平均数（次）
中位数（次）
众数（次）
方差
…
该班级男生
3
3
4
2
…
根据你所学过的统计知识，适当计算女生的有关统计量，进而比较该班级男、女生收看“两会”新闻次数的波动大小
26. 阅读对话，解答问题.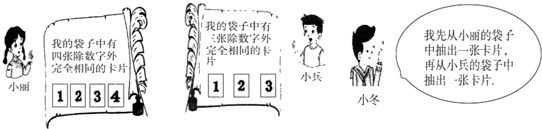
(1)、分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字，请用树状图法或列表法写出（a，b）的所有取值；(2)、小冬抽出（a，b）中使关于x的一元二次方程x2﹣ax+2b＝0根为有理数的是小丽赢，方程的根为无理数的是小兵赢，你觉得游戏是否公平？若公平，请说明理由；若不公平，请修改游戏方案.