浙教版备考2021年中考数学三轮冲刺复习专题1 圆
试卷更新日期：2021-05-16 类型：三轮冲刺
一、单选题
-
1. 如图，正六边形ABCDEF内接于⊙O，点P是 上的任意一点，则∠APB的大小是（ ）
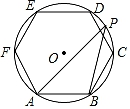A、15° B、30° C、45° D、60°2. 如图，四边形ABCD内接于半径为6的⊙O中，连接AC，若AB＝CD，∠ACB＝45°，∠ACD＝ ∠BAC，则BC的长度为（ ）
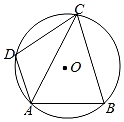A、6 B、6 C、9 D、93. 如图，点O1是△ABC的外心，以AB为直径作⊙O恰好过点O1 ， 若AC＝2，BC＝4 ，则AO1的长是（ ）
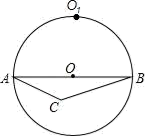A、3 B、 C、2 D、24. 如图，在平面直角坐标系中，正方形 ABCO 的顶点 A，C 分别在 y 轴、x 轴上，以 AB 为弦的⊙M 与 x 轴相切，若点 A 的坐标（0，8），则圆心M 的坐标为（ ）
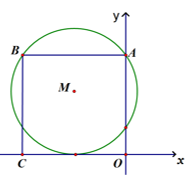A、（－4，3） B、（－3，4） C、（－5，5） D、（－4，5）5. 如图，线段AB经过⊙O的圆心，AC，BD分别与⊙O相切于点C，D.若AC＝BD＝4，∠A＝45°，则 的长度为（ ）
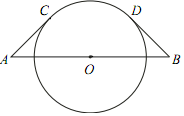A、π B、2π C、2 π D、4π6. 如图，直线PA、PB、MN分别与 O相切于点A，B，D，PA=PB=8cm，则△PMN的周长为（ ）
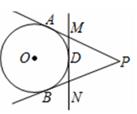A、8cm B、 cm C、16cm D、 cm7. 在直角坐标系中，⊙O的圆心在原点，半径为3，⊙A的圆心A的坐标为(﹣ ，1)，半径为1，那么⊙O与⊙A的位置关系是（ ）A、内含 B、内切 C、相交 D、外切8. 如图，将边长为3的正六边形铁丝框ABCDEF（面积记为S1）变形为以点D为圆心，CD为半径的扇形（面积记为S2），则S1与S2的关系为（ ）
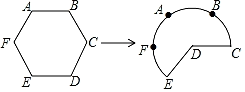A、S1＞S2 B、S1＝S2 C、S1＜S2 D、S1＝ S29. 如图，抛物线y＝ x2﹣1与x轴交于A，B两点，D是以点C（0，4）为圆心，1为半径的圆上的动点，E是线段AD的中点，连接OE，BD，则线段OE的最小值是（ ）
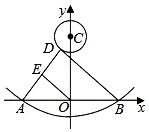A、 B、 C、3 D、210. 已知⊙O的半径为3，A为圆内一定点，AO＝1，P为圆上一动点，以AP为边作等腰△APQ，AP＝PQ，∠APQ＝120°，则OQ的最大值为（ ）A、 B、 C、 D、二、填空题
-
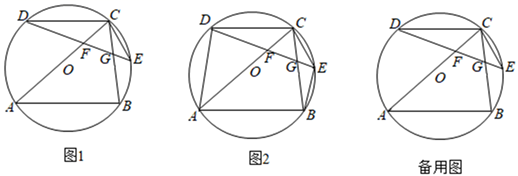
11. 如图，已知半⊙O的直径AB为3，弦AC与弦BD交于点E，OD⊥AC，垂足为点F，AC＝BD，则弦AC的长为.
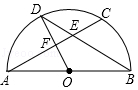12. 如图，⊙O是△ABC的外接圆，AE平分∠BAC交⊙O于点E，交BC于点D，过点E做直线l∥BC． 若∠ABC的平分线BF交AD于点F， DE=4，DF=3，则AF的长为 ．
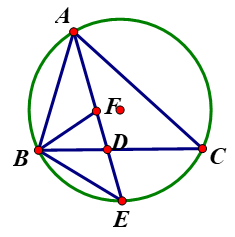13. 如图，AB是⊙O的直径，点C，D，E在⊙O上，若∠AEC＝40°，则∠BDC的度数为.
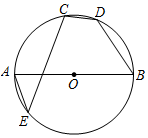14. 如图所示，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，若以点C为圆心，r为半径的圆与边AB所在直线有公共点，则r的取值范围为.
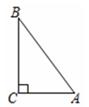15. 如图，Rt△ABC中，∠ABC＝90°，点D是BC边上一点，以BD为直径的半圆与边AC相切于点E.若AB＝3，BC＝4，则BD＝.
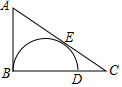16. 如图所示， 内切△ABC ，切点分别为 ， ， ， 切 于 点，交 ， 于点 ， ，若△ABC 的周长为12，BC=2，则△ADE 的周长是 ．
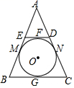17. 如图是一个圆锥形冰淇淋外壳(不计厚度)，已知其母线长为12cm，底面圆半径为3cm，则这个冰淇淋外壳的侧面积等于cm2.
18. 如图，圆柱的侧面是由一张长16πcm、宽3cm的长方形纸条围成（接缝处重叠部分忽略不计），那么该圆柱的体积是cm3.
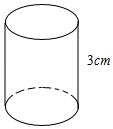
三、综合题
-
19. 如图，已知矩形ABCD是一空旷场地上的小屋示意图，其中AB：AD＝2：1．拴住小狗的绳子一端固定在点A处，请根据下面条件分别画出小狗在小屋外最大活动区域．（小狗的大小不计）
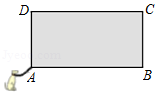
图1 图2(1)、若拴小狗的绳子长度与AD边长相等，在图1中画出小狗在屋外活动的最大区域；(2)、若拴小狗的绳子长度与AB边长相等，在图2中画出小狗在屋外活动的最大区域．20. 如图，AB是⊙O的直径，弦CD⊥AB于点E ，G是弧AC上的点，AG，DC延长线交于点F.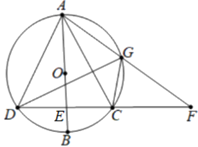
(1)、求证：∠FGC=∠AGD.(2)、若BE=2，CD=8，求AD的长.21. 如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，G是弧AC上的任意一点，AG，DC的延长线相交于点F.
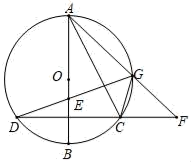(1)、若CD＝8，BE＝2，求⊙O的半径；(2)、求证：∠FGC＝∠AGD；(3)、若直径AB＝10，tan∠BAC＝ ，弧AG＝弧BG，求DG的长.22. 如图（1），正五边形ABCDE与⊙O相切于点A，点C在⊙O上．
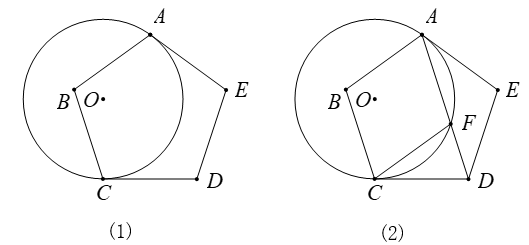(1)、求证：CD是⊙O的切线；(2)、若⊙O的半径为5，求劣弧AC的长度；(3)、如图（2），连接AD交⊙O于点F．求证：四边形ABCF是菱形．23. 如图，在菱形ABCD中，∠A=60°，经过点C且半径为2的⊙O分别切AB，AD于点B，D。
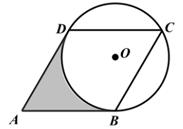(1)、求 的度数。(2)、求图中阴影部分的面积。
24. 如图①是一个小箱子ABCDE放在桌面MN上的示意图，BC这部分可弯曲，在弯曲时形成一段圆弧，设圆弧所在圆的圆心为O，线段AB，CD均与圆弧相切，点B，C分别为切点，小箱子盖面CD与桌面MN平行，此时CD距离桌面14cm，已知AB的长10cm，CD的长为25.2cm.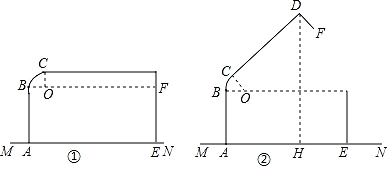
(1)、如图①，求弧BC的长度（结果保留π）.(2)、如图②，若小箱子ABCDE打开后弧BC所对的圆心角度数为60°，求小箱子顶端D到桌面MN的距离DH（结果保留一位小数）.（参考数据： ≈1.73）25. 如图，已知AB是⊙O的直径，点C、D在⊙O上，点E在⊙O外，∠EAC=∠D=60°，AC=6.
(1)、求证：AE是⊙O的切线；(2)、求弦AC与劣弧AC围成弓形的面积；(3)、当CD平分∠BCA时，求△ACD的面积。26. 已知：⊙O的两条弦AB，CD相交于点M，且AB=CD．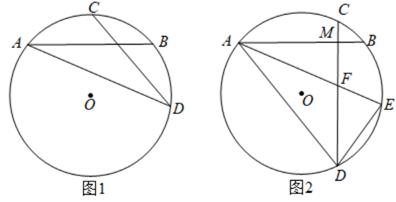
(1)、如图1，连接AD．求证：AM=DM．(2)、如图2，若AB⊥CD，在弧BD上取一点E，使弧BE=弧BC，AE交CD于点F，连AD、DE．①利断∠E与∠DFE是否相等，并说明理由．
②若DE=7，AM+MF=17，求△ADF的面积．
