山东省济南市历城区2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 的相反数是( )A、 B、 C、 D、2. 下列几何体由5个相同的小正方体搭成,其左视图是( )
 A、
A、 B、
B、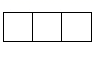 C、
C、 D、
D、 3. 世界最大的单口径球面射电望远镜(FAST)被誉为“中国天眼”,在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为 秒.数据 用科学记数法可以表示为( )
3. 世界最大的单口径球面射电望远镜(FAST)被誉为“中国天眼”,在其新发现的脉冲星中有一颗毫秒脉冲星的自转周期为 秒.数据 用科学记数法可以表示为( ) A、 B、 C、 D、4. 如图, , ,垂足为B , ,则 的度数为( )
A、 B、 C、 D、4. 如图, , ,垂足为B , ,则 的度数为( ) A、 B、 C、 D、5. 下面图形中,是轴对称图形的是( )A、
A、 B、 C、 D、5. 下面图形中,是轴对称图形的是( )A、 B、
B、 C、
C、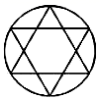 D、
D、 6. 某校举办体能比赛,其中一项是引体向上,每完成一次记录1分,达到10个即为满分10分.甲、乙两班各出代表10个人,比赛成绩分别如下,根据表格中的信息判断,下列结论正确的是( )
6. 某校举办体能比赛,其中一项是引体向上,每完成一次记录1分,达到10个即为满分10分.甲、乙两班各出代表10个人,比赛成绩分别如下,根据表格中的信息判断,下列结论正确的是( )甲班成绩
7
8
9
10
人数
2
2
3
3
乙班成绩
7
8
9
10
人数
1
2
3
4
A、甲班成绩的众数是10分 B、乙班成绩的中位数是9分 C、甲班的成绩的平均数是8.6分 D、乙班成绩的方差是27. 不等式组 的解集在数轴上表示正确的是( )A、 B、
B、 C、
C、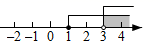 D、
D、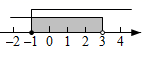 8. 如图,在平面直角坐标系中,点 的坐标分别为 , .将线段 平移后A点的对应点是 ,则点B的对应点 的坐标为( )
8. 如图,在平面直角坐标系中,点 的坐标分别为 , .将线段 平移后A点的对应点是 ,则点B的对应点 的坐标为( )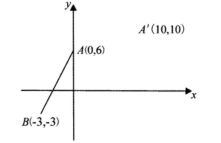 A、 B、 C、 D、9. 国家统计局统计数据 显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为( )A、 B、 C、 D、10. 如图,扇形 的圆心角是直角,半径为 ,C为 边上一点,将 沿 边折叠,圆心O恰好落在弧 上,则阴影部分面积为( )
A、 B、 C、 D、9. 国家统计局统计数据 显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为( )A、 B、 C、 D、10. 如图,扇形 的圆心角是直角,半径为 ,C为 边上一点,将 沿 边折叠,圆心O恰好落在弧 上,则阴影部分面积为( ) A、 B、 C、 D、11. 共享单车为市民出行提供了便利.图1为单车实物图,图2为单车示意图, 与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线 方向调节.已知, , ,车轮半径为 , ,小明体验后觉得当坐垫C离地面高度为 时骑着比较舒适,此时 的长约为( )(结果精确到 ,参考数据: , , )
A、 B、 C、 D、11. 共享单车为市民出行提供了便利.图1为单车实物图,图2为单车示意图, 与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线 方向调节.已知, , ,车轮半径为 , ,小明体验后觉得当坐垫C离地面高度为 时骑着比较舒适,此时 的长约为( )(结果精确到 ,参考数据: , , ) A、 B、 C、 D、12. 函数 ,当 时,此函数的最小值为 ,最大值为1,则m的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、12. 函数 ,当 时,此函数的最小值为 ,最大值为1,则m的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 分解因式:a2+2a= .14. 若一个多边形的内角和是其外角和的3倍,则这个多边形的边数是 .15. 化简: .16. 在一个不透明的盒子中有1个白球和2个红球,它们除颜色外其余都相同,从盒子里任意摸出2个球,则摸出的两个球都是红球的概率是 .17. 甲、乙两人分别从A、B两地出发,相向而行.图中的 , 分别表示甲、乙离B地的距离 与甲出发后所用时间 的函数关系图象,则甲出发小时与乙相遇.
 18. 如图,矩形纸片 , ,点E在线段 上,将 沿 向上翻折,点C的对应点 落在线段 上,点M、N分别是线段 与线段 上的点,将四边形 沿 向下翻折,点A恰好落在线段 的中点 处.则线段 的长为 .
18. 如图,矩形纸片 , ,点E在线段 上,将 沿 向上翻折,点C的对应点 落在线段 上,点M、N分别是线段 与线段 上的点,将四边形 沿 向下翻折,点A恰好落在线段 的中点 处.则线段 的长为 .
三、解答题
-
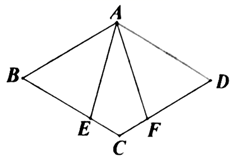
19. 计算:20. 先化简,再求值: ,其中 .21. 已知:如图,在菱形 中,E , F分别在边 , 上,且 ,求证: .
 22. 某学校九年级共400名男生,为了解实心球训练情况,从中随机抽取20名学生的实心球成绩作为样本,数据统计如下(单位:米):
22. 某学校九年级共400名男生,为了解实心球训练情况,从中随机抽取20名学生的实心球成绩作为样本,数据统计如下(单位:米):9.6;5;8.6;8.3;9.5;10.3;7.2;6;5.4;7.7;7.6;5.1;12.5;5.5;7.4;7.3;8.1;10.2;9.3;4.8
根据数据绘制了如下的表格和统计图:
换算为体考分数
成绩(米)
频数
10
4
8
a
6
7
4
b
合计
20
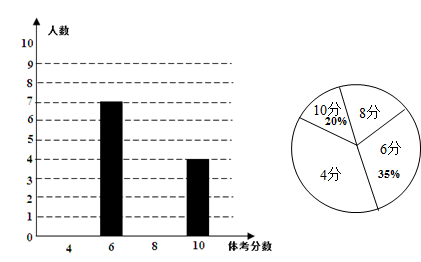
根据上面提供的信息,回答下列问题:
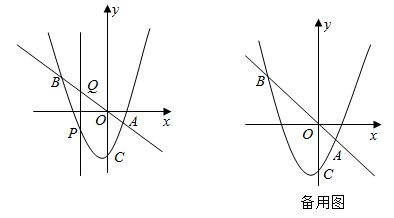
(1)、统计表中的 , ;(2)、请补全条形统计图;(3)、在扇形统计图中,“8分”对应的圆心角的度数是;(4)、根据抽样调查结果,请估计该校九年级学生实心球体考分数不低于8分的有多少人?23. 如图,已知 , ,以 为直径作 ,交 于点D , 过D点作 的切线交边 于点C , 交 的延长线于点P . (1)、求证: ;(2)、如果 ,求 的长.24. 某学校为了增强学生体质,加强体育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.(1)、求购买一根跳绳和一个毽子分别需要多少元;(2)、某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买方案.25. 如图,直线 与双曲线 的交点为 ,与x轴的交点为 ,点C为双曲线 上的一点.
(1)、求证: ;(2)、如果 ,求 的长.24. 某学校为了增强学生体质,加强体育锻炼,决定让各班购买跳绳和毽子作为活动器材.已知购买2根跳绳和5个毽子共需32元;购买4根跳绳和3个毽子共需36元.(1)、求购买一根跳绳和一个毽子分别需要多少元;(2)、某班需要购买跳绳和毽子的总数量是54,且购买的总费用不能超过260元;若要求购买跳绳的数量多于20根,通过计算说明共有哪几种购买方案.25. 如图,直线 与双曲线 的交点为 ,与x轴的交点为 ,点C为双曲线 上的一点.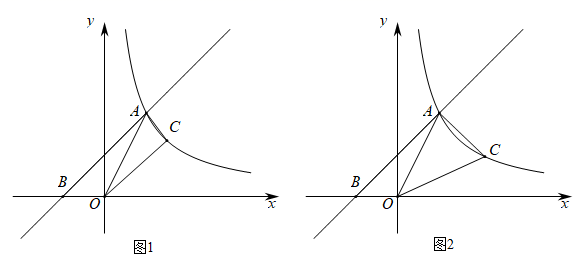 (1)、求a的值及反比例函数的表达式;(2)、如图1,当 时,求 的面积;(3)、如图2,当 时,求点C的坐标.
(1)、求a的值及反比例函数的表达式;(2)、如图1,当 时,求 的面积;(3)、如图2,当 时,求点C的坐标.