云南省曲靖市罗平县2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 如图所示的物体的左视图是( ).
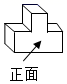 A、
A、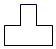 B、
B、 C、
C、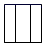 D、
D、 2. 11月1日,随着第七次全国人口普查标准时点到来,第七次全国人口普查正式开启现场登记,约8000000普查人员走入千家万户.数据8000000用科学记数法可表示为( )A、 B、 C、 D、3. 下列运算中,正确的是( )A、 B、 C、 D、4. 正六边形的外角和是( )A、 B、 C、 D、5. 下列说法中,正确的是( )A、“三角形中,任意两边之和大于第三边”属于必然事件 B、随机投掷一枚质地均匀的硬币20次,全是正面朝上,那么第21次投掷这枚硬币,一定是正面朝上 C、为了解某班学生身高情况,可随机抽取10名男生的身高进行调查 D、为了解今年十月份本县的气温变化情况,适合选用条形统计图进行分析6. 一组按此规律排列的式子: ,…,则第n个式子是( )A、 B、 C、 D、7. 已知一个圆锥的侧面展开图是一个半圆,则该圆锥的母线与底面半径所成角的度数是( )A、 B、 C、 D、8. 若分式方程 无解,则实数a的值为( )A、1 B、1或 C、 D、1或2
2. 11月1日,随着第七次全国人口普查标准时点到来,第七次全国人口普查正式开启现场登记,约8000000普查人员走入千家万户.数据8000000用科学记数法可表示为( )A、 B、 C、 D、3. 下列运算中,正确的是( )A、 B、 C、 D、4. 正六边形的外角和是( )A、 B、 C、 D、5. 下列说法中,正确的是( )A、“三角形中,任意两边之和大于第三边”属于必然事件 B、随机投掷一枚质地均匀的硬币20次,全是正面朝上,那么第21次投掷这枚硬币,一定是正面朝上 C、为了解某班学生身高情况,可随机抽取10名男生的身高进行调查 D、为了解今年十月份本县的气温变化情况,适合选用条形统计图进行分析6. 一组按此规律排列的式子: ,…,则第n个式子是( )A、 B、 C、 D、7. 已知一个圆锥的侧面展开图是一个半圆,则该圆锥的母线与底面半径所成角的度数是( )A、 B、 C、 D、8. 若分式方程 无解,则实数a的值为( )A、1 B、1或 C、 D、1或2二、填空题
-
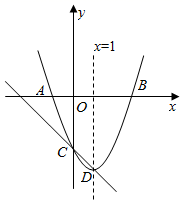
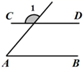
9. -9的相反数是 .10. 因式分解:3x2﹣12= .11. 如图, , ,则 .
 12. 若点 和点 都在反比例函数 的图象上,则k的值为 .13. 在矩形 中,对角线 和 相交于点O,过点B作 的垂线,垂足为E,若 , ,则线段 的长为 .
12. 若点 和点 都在反比例函数 的图象上,则k的值为 .13. 在矩形 中,对角线 和 相交于点O,过点B作 的垂线,垂足为E,若 , ,则线段 的长为 .三、解答题
-
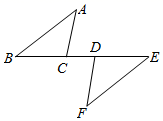
14. 计算: .15. 如图,B、C、D、E在同一条直线上; .求证: .
 16. 为了迎接2021年云南省初中学业水平考试,某校为了了解九年级两个重点班在本次模拟考试中的数学成绩情况,随机抽取了甲、乙两班各20名同学的数学成绩进行整理分析,下列给出了部分信息:
16. 为了迎接2021年云南省初中学业水平考试,某校为了了解九年级两个重点班在本次模拟考试中的数学成绩情况,随机抽取了甲、乙两班各20名同学的数学成绩进行整理分析,下列给出了部分信息:信息一:甲、乙两班同学的样本成绩分布如下:
班级
甲
0
0
4
3
7
4
2
乙
2
0
0
4
6
5
3
信息二:甲班样本成绩在90~100一组的是:91,92,93,95,96,98,99
信息三:甲、乙两班样本成绩的平均数、中位数、优秀率如下:
班级
平均数
中位数
优秀率
甲
94.7
a
b
乙
93.3
97
根据以上信息,回答下列问题:
(1)、上述表中a= , b= ;(2)、小明的成绩在此次抽样调查中,与他所在的班级相比,小明的成绩高于平均数,却排在了后十名,则小明是班的学生;(3)、根据样本数据,你认为哪个班级的数学模拟成绩更好,请说明理由.17. 某水果专卖店在批发市场用740元购进甲、乙两种水果共100千克进行零售,已知甲种水果购进单价为5元,乙种水果购进单价为8元.该水果店购买了甲、乙两种水果各多少千克?18. 甲、乙、丙、丁四个人玩扑克牌游戏,他们先取出两张红桃和两张黑桃共四张扑克牌,洗匀后背面朝上放在桌面上,每人抽取其中一张,拿到相同颜色扑克牌的两个人为游戏搭档.(1)、求甲抽取一张扑克牌刚好是红桃的概率;(2)、若甲、乙两人各抽取了一张扑克牌,求两人恰好成为游戏搭档的概率.19. 如图,在▱ABCD中,∠ABC=60°,BC=2AB , 点E、F分别是BC、DA的中点.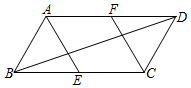 (1)、求证:四边形AECF是菱形;(2)、若AB=2,求BD的长.20. 为了巩固拓展脱贫攻坚成果,开启乡村振兴发展之门,某村合作社组织20辆汽车装运A、B两种土特产到外地销售,规定每辆汽车只能装运一种特产,且必须装满;装运每种特产的汽车不少于4辆.设用x辆汽车装运A特产,此次外销获得的利润为y , 根据下表提供的信息,解答下列问题:
(1)、求证:四边形AECF是菱形;(2)、若AB=2,求BD的长.20. 为了巩固拓展脱贫攻坚成果,开启乡村振兴发展之门,某村合作社组织20辆汽车装运A、B两种土特产到外地销售,规定每辆汽车只能装运一种特产,且必须装满;装运每种特产的汽车不少于4辆.设用x辆汽车装运A特产,此次外销获得的利润为y , 根据下表提供的信息,解答下列问题:土特产
A
B
每辆汽车装运量(吨)
5
4
每吨特产获利(万元)
0.6
0.8
(1)、求y与x之间的函数关系式,并写出自变量的取值范围;(2)、由于市场需要,将A特产每吨售价提高 万元,求该合作社应该怎样装运销售这批土特产,可获得最大利润,最大利润是多少?