云南省昆明市西山区2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
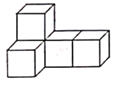
1. 如图是由大小相同的正方体搭成的几何体,其主视图是( )
 A、
A、 B、
B、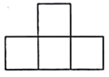 C、
C、 D、
D、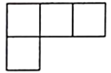 2. 函数 的自变量x的取值范围是( )A、 B、 C、 D、3. 下列说法正确的是( )A、为了了解全国初中学生的眼睛近视情况,适宜采用全面调查; B、“每天太阳从西边出来”是随机事件; C、甲、乙两人射中环数的方差分别为 , ,说明甲的射击成绩比乙稳定; D、数据3,4,2,5,6的平均数是4.4. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的的实数根 C、没有实数根 D、无法判断5. 在平面直角坐标系中,线段 两端点的坐标分别是 , ,平移后得到线段 ,A点的对应点坐标 ,则 的坐标为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,在 中, , 轴,点A在反比例函数 的图象上.若点B在y反比例函数 的图象上,则k的值为( )
2. 函数 的自变量x的取值范围是( )A、 B、 C、 D、3. 下列说法正确的是( )A、为了了解全国初中学生的眼睛近视情况,适宜采用全面调查; B、“每天太阳从西边出来”是随机事件; C、甲、乙两人射中环数的方差分别为 , ,说明甲的射击成绩比乙稳定; D、数据3,4,2,5,6的平均数是4.4. 一元二次方程 的根的情况是( )A、有两个相等的实数根 B、有两个不相等的的实数根 C、没有实数根 D、无法判断5. 在平面直角坐标系中,线段 两端点的坐标分别是 , ,平移后得到线段 ,A点的对应点坐标 ,则 的坐标为( )A、 B、 C、 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,在 中, , 轴,点A在反比例函数 的图象上.若点B在y反比例函数 的图象上,则k的值为( )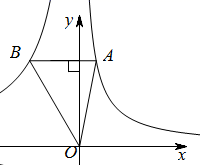 A、 B、 C、3 D、-38. 如图,有公共顶点O的两个边长为3的正五边形(不重叠),以O点为圆心,半径为3作圆,构成一个“蘑菇”形图案,则这个“蘑菇”形图案(阴影部分)的面积为( )
A、 B、 C、3 D、-38. 如图,有公共顶点O的两个边长为3的正五边形(不重叠),以O点为圆心,半径为3作圆,构成一个“蘑菇”形图案,则这个“蘑菇”形图案(阴影部分)的面积为( )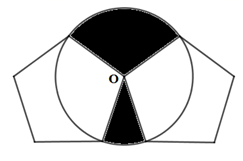 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
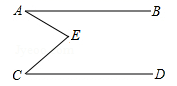
9. 数轴上表示-2的点与原点的距离是 .10. 分解因式: .11. 如图, ,则 , ,则 的度数为°.
 12. 我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,832个贫困县全部摘帽,128000个贫困村全部出列,完成了消除绝对贫困的艰巨任务,创造了又一个彪炳史册的人间奇迹.将数字128000用科学记数法表示为 .13. 下列图形都是由同样大小的圆点按照一定规律所组成的,其中第一个图形中一共有3个圆点,第二个图形中一共有8个圆点,第三个图形中一共有15个圆点,…,按此规律排列下去,第10个图形中圆点的个数为 .
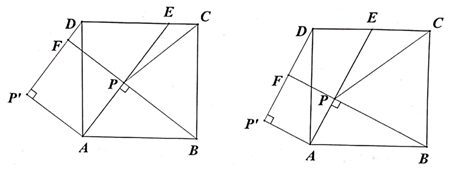
12. 我国脱贫攻坚战取得了全面胜利,现行标准下9899万农村贫困人口全部脱贫,832个贫困县全部摘帽,128000个贫困村全部出列,完成了消除绝对贫困的艰巨任务,创造了又一个彪炳史册的人间奇迹.将数字128000用科学记数法表示为 .13. 下列图形都是由同样大小的圆点按照一定规律所组成的,其中第一个图形中一共有3个圆点,第二个图形中一共有8个圆点,第三个图形中一共有15个圆点,…,按此规律排列下去,第10个图形中圆点的个数为 . 14. 如图,有互相垂直的两面墙 , ,梯子 ,两端点A , B分别在两面墙上滑动( 长度不变),P为 的中点,柱子 ,底端C到墙角O的距离为6m.在此滑动过程中,点D到点P的距离的最小值为m.
14. 如图,有互相垂直的两面墙 , ,梯子 ,两端点A , B分别在两面墙上滑动( 长度不变),P为 的中点,柱子 ,底端C到墙角O的距离为6m.在此滑动过程中,点D到点P的距离的最小值为m.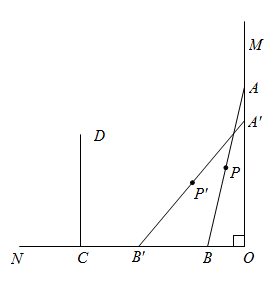
三、解答题
-
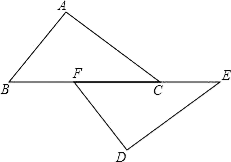
15. 先化简,再求值: ,其中 .16. 如图,已知:点B、F、C、E在一条直线上,∠B=∠E,BF=CE,AC∥DF.求证:△ABC≌△DEF.
 17. 为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: )进行了测量.根据统计的结果,绘制出如图的统计图①和图②.
17. 为了解某种小麦的长势,从中随机抽取了部分麦苗,对苗高(单位: )进行了测量.根据统计的结果,绘制出如图的统计图①和图②.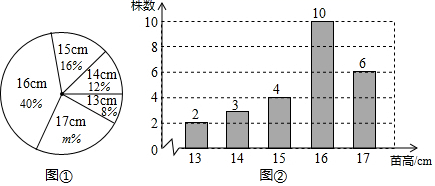
请根据相关信息,解答下列问题:
(1)、本次抽取的麦苗的株数为 , 这组苗高数据的众数为 , 中位数为 .(2)、求统计的这组苗高数据的平均数及m的值.18. 中国高铁已成为一张世界名片.经过技术改进,某次列车平均提速20 ,列车提速前行驶540 所用的时间,提速后比提速前可多行驶60 ,求这次列车提速前的平均速度.19. 为弘扬传统民族文化,某校开设了“民族美食制作”,“曲艺歌舞赏析”,“方言传承研究”三个兴趣小组(分别用字母A , B , C表示),每个同学只能参加一个兴趣小组,老师将A , B , C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,小红先从中随机抽取一张卡片,放回后洗匀,再由小明从中随机抽取一张卡片.(1)、小红抽中“民族美食制作”兴趣小组的概率是;(2)、试用画树状图或列表的方法(选其中一种即可)表示所有可能的结果,并求出小红和小明抽中相同的兴趣小组的概率.20. 某超市需购进某种商品,每件的进价10元.设该商品的销售单价为x(单位:元/件),在销售过程中发现:当 时,该商品的日销售量y(单位:件)与销售单价x之间存在一次函数关系,x , y之间的部分数值对应关系如下表:销售单价x(元/件)
10
20
日销售量y(件)
180
120
(1)、请求出当 时,y与x之间的函数关系式;(2)、设该商品的日销售利润为w元,当该商品的销售单价x(元/件)定价为多少元时,日销售利润最大?最大利润是多少?21. 如图,在5×8的正方形网格中,每个小正方形的边长为1,在格点上分别有两点O , C . (1)、操作:在网格中作一条线段 (点P在格点上),再以点C为直角顶点作一个格点三角形 ,使 , , ;(2)、探索:以O为圆心, 为半径作 ,请判断直线 与 的位置关系,并说明理由.
(1)、操作:在网格中作一条线段 (点P在格点上),再以点C为直角顶点作一个格点三角形 ,使 , , ;(2)、探索:以O为圆心, 为半径作 ,请判断直线 与 的位置关系,并说明理由.