天津市东丽区2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 计算 的值是( )A、 B、6 C、 D、122. 2cos45°的值等于( )A、1 B、 C、 D、23. 在3月份市民政局召开的全市基金会脱贫攻坚总结会上获悉,过去的三年,全市社会组织积极作为,全力投入脱贫攻坚事业,共有779家社会组织承接扶贫项目673个,帮扶资金总计达174000000元,数字174000000用科学记数法表示应为( )A、 B、 C、 D、4. 在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 如图,是一个由5个相同的正方体组成的立体图形,它的左视图是( )
5. 如图,是一个由5个相同的正方体组成的立体图形,它的左视图是( )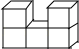 A、
A、 B、
B、 C、
C、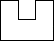 D、
D、 6. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间7. 计算 的结果是( )A、5 B、 C、 D、8. 如图,四边形 为菱形,A , B两点的坐标分别是 ,点C , D在坐标轴上,则菱形 的周长等于( )
6. 估计 的值在( )A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间7. 计算 的结果是( )A、5 B、 C、 D、8. 如图,四边形 为菱形,A , B两点的坐标分别是 ,点C , D在坐标轴上,则菱形 的周长等于( ) A、 B、 C、 D、9. 方程组 的解是( )A、 B、 C、 D、10. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、11. 如图,有一张矩形纸条 ,点M , N分别在边 上, .现将四边形 沿 折叠,使点B , C分别落在点 上.当点 恰好落在边 上时,下列结论不一定正确的是( )
A、 B、 C、 D、9. 方程组 的解是( )A、 B、 C、 D、10. 若点 都在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、11. 如图,有一张矩形纸条 ,点M , N分别在边 上, .现将四边形 沿 折叠,使点B , C分别落在点 上.当点 恰好落在边 上时,下列结论不一定正确的是( ) A、 B、 C、 D、12. 二次函数 (a , b , c是常数, )经过点 ,且 .当 时,y随x的增大而增大.下列结论:① :②若点 在抛物线上,则 :③ 其中,正确结论的个数是( )A、0 B、1 C、2 D、3
A、 B、 C、 D、12. 二次函数 (a , b , c是常数, )经过点 ,且 .当 时,y随x的增大而增大.下列结论:① :②若点 在抛物线上,则 :③ 其中,正确结论的个数是( )A、0 B、1 C、2 D、3二、填空题
-
13. 计算 的结果是 .14. 计算 的结果等于 .15. 不透明袋子中装有13个球,其中有3个红球、4个绿球和6个蓝球,这些球除颜色外无其他差别.从袋子中随机取出1个球,则它是绿球的概率是 .16. 直线 与y轴交点坐标为 .17. 如图,正方形 和 , , ,连接 , .若 绕点A旋转,当 最大时, .
 18. 如图,是由边长为1的小正方形组成的 的网格, 的顶点都在格点上,请仅用无刻度的直尺作图.
18. 如图,是由边长为1的小正方形组成的 的网格, 的顶点都在格点上,请仅用无刻度的直尺作图. (1)、线段 的长等于;(2)、请在如图所示的网格中,用无刻度的直尺,画出一个格点P , 使 并简要说明画图方法(不要求证明)
(1)、线段 的长等于;(2)、请在如图所示的网格中,用无刻度的直尺,画出一个格点P , 使 并简要说明画图方法(不要求证明)三、解答题
-
19. 解不等式组
请结合题意填空,完成本题的解答.
(1)、解不等式①,得 .(2)、解不等式②,得 .(3)、把不等式①和②的解集在数轴上分别表示出来: (4)、原不等式组的解集为 .20. 某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如下统计图.
(4)、原不等式组的解集为 .20. 某校为了了解初中学生每天的睡眠时间(单位为小时),随机调查了该校的部分初中学生,根据调查结果,绘制出如下统计图.
请根据相关信息,解答下列问题:
(1)、扇形统计图中的 , 条形统计图中的 ;(2)、求所调查的初中学生每天睡眠时间的平均数、众数和中位数,21. 如图, 是 直径, 是 的弦, . (1)、如图1,求 的度数;(2)、如图2.过点C作 的切线,与 的延长线相交于点E , 求 的大小.22. 如图,小山上有一座 高的电视发射塔 ,为了测量小山的高度 .在山脚某处D测得山顶的仰角为 ,测得塔项的仰角为 ,求小山的高.(已知: )(结果精确到 )
(1)、如图1,求 的度数;(2)、如图2.过点C作 的切线,与 的延长线相交于点E , 求 的大小.22. 如图,小山上有一座 高的电视发射塔 ,为了测量小山的高度 .在山脚某处D测得山顶的仰角为 ,测得塔项的仰角为 ,求小山的高.(已知: )(结果精确到 ) 23. 小明骑自行车保持匀速从甲地到乙地,到达乙地后,休息了一段时间,然后以相同的速度原路返回,停在甲地.设小明出发 后,到达距离甲地 的地方,图中的折线表示的是y与x之间的函数关系.
23. 小明骑自行车保持匀速从甲地到乙地,到达乙地后,休息了一段时间,然后以相同的速度原路返回,停在甲地.设小明出发 后,到达距离甲地 的地方,图中的折线表示的是y与x之间的函数关系. (1)、根据题意填空:甲、乙两地的距离m , ;(2)、求小明从乙地返回甲地过程中,y与x之间的函数关系式:(3)、在小明从甲地出发的同时,小红从乙地步行至甲地,保持 的速度不变,到甲地停止.小明从甲地出发 与小红相距 ?24. 在平面直角坐标系中,点A的坐标为 ,点B的坐标为 ,把 绕原点O顺时针旋转,得到 ,记旋转角为 .
(1)、根据题意填空:甲、乙两地的距离m , ;(2)、求小明从乙地返回甲地过程中,y与x之间的函数关系式:(3)、在小明从甲地出发的同时,小红从乙地步行至甲地,保持 的速度不变,到甲地停止.小明从甲地出发 与小红相距 ?24. 在平面直角坐标系中,点A的坐标为 ,点B的坐标为 ,把 绕原点O顺时针旋转,得到 ,记旋转角为 . (1)、如图①,当 时,求点 的坐标.(2)、设直线 与直线 相交于点M , 如图②,当 时,求 的面积.25. 如图,在平面直角坐标系中,直线 与x轴交于点C,与抛物线 交于点A,此抛物线与x轴的正半轴交于点 ,且 .
(1)、如图①,当 时,求点 的坐标.(2)、设直线 与直线 相交于点M , 如图②,当 时,求 的面积.25. 如图,在平面直角坐标系中,直线 与x轴交于点C,与抛物线 交于点A,此抛物线与x轴的正半轴交于点 ,且 . (1)、求抛物线的解析式;(2)、点P是直线 上方抛物线上的一点.过点P作 垂直于x轴于点D,交线段 于点E,使 .
(1)、求抛物线的解析式;(2)、点P是直线 上方抛物线上的一点.过点P作 垂直于x轴于点D,交线段 于点E,使 .①求点P的坐标;
②在直线 上是否存在点M,使 为以 为直角边的直角三角形?若存在,直接写出符合条件的点M的坐标;若不存在,说明理由.