山东省邹城市2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 如果a与 互为倒数,那么a是( )A、 B、 C、 D、22. 下列等式成立的是( )A、 B、 C、 D、3. 函数y= 的自变量x的取值范围在数轴上可表示为( )A、
 B、
B、 C、
C、 D、
D、 4. 如图是某几何体的三视图,该几何体是( )
4. 如图是某几何体的三视图,该几何体是( )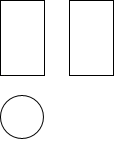 A、圆柱 B、正方体 C、圆锥 D、球5. 若关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是( )A、 B、 C、 且 D、 且6. 如图,菱形 的对角线的长分别为2和5,P是对角线 上任一点(点P不与点A,C重合),且 交 于E, 交 于F,则阴影部分的面积是( )
A、圆柱 B、正方体 C、圆锥 D、球5. 若关于x的一元二次方程 有两个不相等的实数根,则k的取值范围是( )A、 B、 C、 且 D、 且6. 如图,菱形 的对角线的长分别为2和5,P是对角线 上任一点(点P不与点A,C重合),且 交 于E, 交 于F,则阴影部分的面积是( ) A、10 B、7.5 C、5 D、2.57. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、
A、10 B、7.5 C、5 D、2.57. 已知抛物线y=ax2+bx+c与反比例函数y= 的图象在第一象限有一个公共点,其横坐标为1,则一次函数y=bx+ac的图象可能是( )A、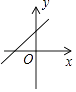 B、
B、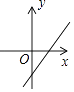 C、
C、 D、
D、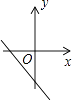 8. 如图,P点的坐标为(3,2),过P点的直线 分别交x轴和y轴的正半轴于A,B两点,作 轴于M点,作 轴于N点,若 的面积与 的面积的比为 ,则直线 的解析式为( )
8. 如图,P点的坐标为(3,2),过P点的直线 分别交x轴和y轴的正半轴于A,B两点,作 轴于M点,作 轴于N点,若 的面积与 的面积的比为 ,则直线 的解析式为( ) A、 B、 C、 D、9. 一种商品进价为每件a元,按进价增加25%出售,后因库存积压降价,按售价的九折出售,每件还盈利( )A、0.125a元 B、0.15a元 C、0.25a元 D、1.25a元10. 如图,平面直角坐标系中, 是边长为2的等边三角形,作 与 关于点 成中心对称,再作 与 关于点 成中心对称,如此作下去,则 (n是正整数)的顶点 的坐标是( )
A、 B、 C、 D、9. 一种商品进价为每件a元,按进价增加25%出售,后因库存积压降价,按售价的九折出售,每件还盈利( )A、0.125a元 B、0.15a元 C、0.25a元 D、1.25a元10. 如图,平面直角坐标系中, 是边长为2的等边三角形,作 与 关于点 成中心对称,再作 与 关于点 成中心对称,如此作下去,则 (n是正整数)的顶点 的坐标是( ) A、( , ) B、( , ) C、( , ) D、( , )
A、( , ) B、( , ) C、( , ) D、( , )二、填空题
-
11. 已知一粒米的质量是0.000021千克,这个数字用科学记数法表示为.12. 分解因式: =13. 一个不透明的袋子中装有除颜色外其余均相同的3个红球2个黑球,现从中随机一次摸出两个球恰好一红一黑的概率为 .14. 如图,在 中,点A的坐标为 ,点B的坐标为 ,点C的坐标为 ,如果要使以A,B,D为顶点的三角形与 全等(点D不与点C重合),那么点D的坐标是 .
 15. 如图,在 中, , , ,点D是 上一动点,连结 ,将 沿 折叠,点C落在点C',连结DC'交 于点E,连结AC',BC'.当 是直角三角形时, 的长为 .
15. 如图,在 中, , , ,点D是 上一动点,连结 ,将 沿 折叠,点C落在点C',连结DC'交 于点E,连结AC',BC'.当 是直角三角形时, 的长为 .
三、解答题
-
16. 先化简,再求值: ,其中 , .17. 如图,一次函数 的图象与反比例函数 的图象交于A,B两点,与x轴交于C点.已知A点的坐标为( ,3).
 (1)、求一次函数与反比例函数的解析式;(2)、作 轴,垂足为M,求 的面积.18. 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
(1)、求一次函数与反比例函数的解析式;(2)、作 轴,垂足为M,求 的面积.18. 在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:5640 6430 6520 6798 7325 8430 8215 7453 7446 6754
7638 6834 7326 6830 8648 8753 9450 9865 7290 7850
对这20个数据按组距1000进行分组,并统计整理绘制了如下尚不完整的统计图表:
步数分组统计表
组别
步数分组
频数
A
5500≤x<6500
2
B
6500≤x<7500
10
C
7500≤x<8500
m
D
8500≤x<9500
3
E
9500≤x<10500
n

请根据以上信息解答下列问题:
(1)、填空:m= , n=;(2)、补全频数直方图;(3)、这20名“健步走运动”团队成员一天行走步数的中位数落在组;(4)、若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.19. 如图, 为⊙O的直径,弦 于点M,过B点作 ,交 的延长线于点E,连接 . (1)、求证: 为⊙O的切线;(2)、如果 ,求⊙O的直径.20. 某校在去年购买A , B两种足球,费用分别为2400元和2000元,其中A种足球数量是B种足球数量的2倍,B种足球单价比A种足球单价多80元/个.(1)、求A , B两种足球的单价;(2)、由于该校今年被定为“足球特色校”,学校决定再次购买A , B两种足球共18个,且本次购买B种足球的数量不少于A种足球数量的2倍,若单价不变,则本次如何购买才能使费用W最少?
(1)、求证: 为⊙O的切线;(2)、如果 ,求⊙O的直径.20. 某校在去年购买A , B两种足球,费用分别为2400元和2000元,其中A种足球数量是B种足球数量的2倍,B种足球单价比A种足球单价多80元/个.(1)、求A , B两种足球的单价;(2)、由于该校今年被定为“足球特色校”,学校决定再次购买A , B两种足球共18个,且本次购买B种足球的数量不少于A种足球数量的2倍,若单价不变,则本次如何购买才能使费用W最少?

