山东省枣庄市薛城区2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 方程x2+x-12=0的两个根为( )A、x1=-2,x2=6 B、x1=-6,x2=2 C、x1=-3,x2=4 D、x1=-4,x2=32. 大约在两千四五百年前,如图1墨子和他的学生做了世界上第一个小孔成倒像的实验.并在《墨经》中有这样的精彩记录:“景到,在午有端,与景长,说在端”.如图2所示的小孔成像实验中,若物距为 ,像距为 ,蜡烛火焰倒立的像的高度是 ,则蜡烛火焰的高度是( )
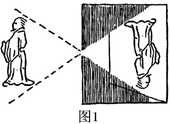
 A、 B、 C、 D、3. 要得到抛物线 ,可以将抛物线 ( )A、向右平移6个单位长度,再向下平移3个单位长度 B、向右平移6个单位长度,再向上平移3个单位长度 C、向左平移6个单位长度,再向上平移3个单位长度 D、向左平移6个单位长度,再向下平移3个单位长度4. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C的大小等于( )
A、 B、 C、 D、3. 要得到抛物线 ,可以将抛物线 ( )A、向右平移6个单位长度,再向下平移3个单位长度 B、向右平移6个单位长度,再向上平移3个单位长度 C、向左平移6个单位长度,再向上平移3个单位长度 D、向左平移6个单位长度,再向下平移3个单位长度4. 如图,AB是⊙O的弦,AC是⊙O的切线,A为切点,BC经过圆心,若∠B=25°,则∠C的大小等于( ) A、25° B、20° C、40° D、50°5. 如图,菱形 的边长为13,对角线 ,点E、F分别是边 、 的中点,连接 并延长与 的延长线相交于点G,则 ( )
A、25° B、20° C、40° D、50°5. 如图,菱形 的边长为13,对角线 ,点E、F分别是边 、 的中点,连接 并延长与 的延长线相交于点G,则 ( )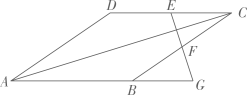 A、13 B、10 C、12 D、56. 图2是图1中长方体的三视图,若用S表示面积,S主=x2+2x , S左=x2+x , 则S俯=( )
A、13 B、10 C、12 D、56. 图2是图1中长方体的三视图,若用S表示面积,S主=x2+2x , S左=x2+x , 则S俯=( )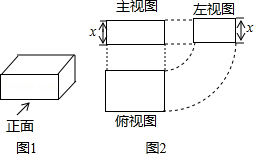 A、x2+3x+2 B、x2+2 C、x2+2x+1 D、2x2+3x7. 如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( )
A、x2+3x+2 B、x2+2 C、x2+2x+1 D、2x2+3x7. 如图,点I为△ABC的内心,AB=4,AC=3,BC=2,将∠ACB平移使其顶点与I重合,则图中阴影部分的周长为( ) A、4.5 B、4 C、3 D、28. 如图①,正方形 中, , 相交于点O,E是 的中点,动点P从点E出发,沿着 的路径以每秒1个单位长度的速度运动到点A,在此过程中线段 的长度 随着运动时间x的函数关系如图②所示,则 的长为( )
A、4.5 B、4 C、3 D、28. 如图①,正方形 中, , 相交于点O,E是 的中点,动点P从点E出发,沿着 的路径以每秒1个单位长度的速度运动到点A,在此过程中线段 的长度 随着运动时间x的函数关系如图②所示,则 的长为( ) A、 B、4 C、 D、9. 如图,△OA1B1 , △A1A2B2 , △A2A3B3 , …是分别以B1 , B2 , B3 , …为直角顶点,斜边在x轴正半轴上的等腰直角三角形,其直角顶点B1(x1 , y1),B2(x2 , y2),B3(x3 , y3),…均在反比例函数y= (>0)的图象上,则y1+y2+y3+…+y10的值为( )
A、 B、4 C、 D、9. 如图,△OA1B1 , △A1A2B2 , △A2A3B3 , …是分别以B1 , B2 , B3 , …为直角顶点,斜边在x轴正半轴上的等腰直角三角形,其直角顶点B1(x1 , y1),B2(x2 , y2),B3(x3 , y3),…均在反比例函数y= (>0)的图象上,则y1+y2+y3+…+y10的值为( )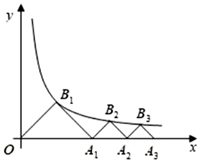 A、 B、6 C、 D、10. 若二次函数y=a2x2﹣bx﹣c的图象,过不同的六点A(﹣1,n)、B(5,n﹣1)、C(6,n+1)、D( ,y1)、E(2,y2)、F(4,y3),则y1、y2、y3的大小关系是( )A、y1<y2<y3 B、y1<y3<y2 C、y2<y3<y1 D、y2<y1<y311. 如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F , 交AB于E , 点G是AE中点且∠AOG=30°,①DC=3OG;②OG= BC;③△OGE是等边三角形;④S△AOE= S矩形ABCD , 则下列结论正确的个数为( )
A、 B、6 C、 D、10. 若二次函数y=a2x2﹣bx﹣c的图象,过不同的六点A(﹣1,n)、B(5,n﹣1)、C(6,n+1)、D( ,y1)、E(2,y2)、F(4,y3),则y1、y2、y3的大小关系是( )A、y1<y2<y3 B、y1<y3<y2 C、y2<y3<y1 D、y2<y1<y311. 如图,在矩形ABCD中,O为AC中点,EF过O点且EF⊥AC分别交DC于F , 交AB于E , 点G是AE中点且∠AOG=30°,①DC=3OG;②OG= BC;③△OGE是等边三角形;④S△AOE= S矩形ABCD , 则下列结论正确的个数为( )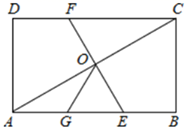 A、1个 B、2个 C、3个 D、4个12. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )
A、1个 B、2个 C、3个 D、4个12. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )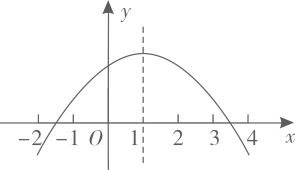 A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 在△ABC中,若 ,∠A、∠B都是锐角,则∠C的度数为.14. 如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度CD为2m,水面宽AB为8m,则输水管的半径为m.
 15. 如果关于x的方 的两个实数根分别为x1 , x2 , 那么 的值为 .16. 如图,平面直角坐标系中,已知O(0,0),A(﹣3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,测第70次旋转结束时,点D的坐标为 .
15. 如果关于x的方 的两个实数根分别为x1 , x2 , 那么 的值为 .16. 如图,平面直角坐标系中,已知O(0,0),A(﹣3,4),B(3,4),将△OAB与正方形ABCD组成的图形绕点O顺时针旋转,每次旋转90°,测第70次旋转结束时,点D的坐标为 . 17. 如图,在反比例函数 的图象上有一点A向x轴垂线交x轴于点C , B为线段AC的中点,又D点在x轴上,且OD=3OC , 则△OBD的面积为 .
17. 如图,在反比例函数 的图象上有一点A向x轴垂线交x轴于点C , B为线段AC的中点,又D点在x轴上,且OD=3OC , 则△OBD的面积为 .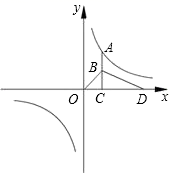 18. 如图,在△ABC中,BA=BC , ∠ABC=90°,AD=DB , BE⊥DC于E , 连接AE并延长交BC与F , 以下说法正确的有 . (直接填序号)
18. 如图,在△ABC中,BA=BC , ∠ABC=90°,AD=DB , BE⊥DC于E , 连接AE并延长交BC与F , 以下说法正确的有 . (直接填序号)①BE=DE•EC;②EA=EB;③AE:EF=3:2;④FC2=FE•FA .
 19. 如图,E , F是正方形ABCD的边AD上两个动点,满足AE=DF . 连接CF交BD于点G , 连接BE交AG于点H . 若正方形的边长为2,则线段DH长度的最小值是 .
19. 如图,E , F是正方形ABCD的边AD上两个动点,满足AE=DF . 连接CF交BD于点G , 连接BE交AG于点H . 若正方形的边长为2,则线段DH长度的最小值是 . 20. 如图,在平面直角坐标系中,点A、B分别在x轴和y轴, ,∠AOB的角平分线与OA的垂直平分线交于点C , 与AB交于点D , 反比例函数y= 的图象过点C . 当以CD为边的正方形的面积为 时,k的值为 .
20. 如图,在平面直角坐标系中,点A、B分别在x轴和y轴, ,∠AOB的角平分线与OA的垂直平分线交于点C , 与AB交于点D , 反比例函数y= 的图象过点C . 当以CD为边的正方形的面积为 时,k的值为 .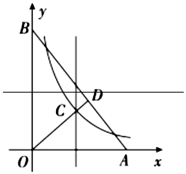
三、解答题
-
21. 如图,放置在水平桌面上的台灯的灯臂AB长为30cm,灯罩BC长为20cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1cm,参考数据: ≈1.732)
 22. 如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E.
22. 如图,△ABC是⊙O的内接三角形,∠BAC=75°,∠ABC=45°.连接AO并延长,交⊙O于点D,连接BD.过点C作⊙O的切线,与BA的延长线相交于点E. (1)、求证:AD∥EC;(2)、若AB=12,求线段EC的长.23. 阅读材料:已知方程p2﹣p﹣1=0,1﹣q﹣q2=0且pq≠1,求 的值.
(1)、求证:AD∥EC;(2)、若AB=12,求线段EC的长.23. 阅读材料:已知方程p2﹣p﹣1=0,1﹣q﹣q2=0且pq≠1,求 的值.解:由p2﹣p﹣1=0,及1﹣q﹣q2=0可知p≠0,
又∵pq≠1,
∴p≠ .
∵1﹣q﹣q2=0可变形为 ﹣1=0,
根据p2﹣p﹣1=0和 ﹣1=0的特征,
∴p、 是方程x2﹣x﹣1=0的两个不相等的实数根,
则p+ ,即 .
根据阅读材料所提供的方法,完成下面的解答.
已知:2m2﹣5m﹣1=0, ,且m≠n , 求:
(1)、mn的值;(2)、 .24. 如图,在平面直角坐标系xOy中,函数 的图像与函数 (x<0)的图像相交于点A(﹣1,6),并与x轴交于点C.点D是线段AC上一点,△ODC与△OAC的面积比为2:3.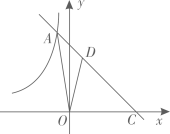 (1)、k= , b=;(2)、求点D的坐标;(3)、若将△ODC绕点O逆时针旋转,得到△OD′C′,其中点D′落在x轴负半轴上,判断点C′是否落在函数 (x<0)的图像上,并说明理由.25. 如图,在平行四边形 中, 是对角线, ,以点A为圆心,以 的长为半径作 ,交 边于点E,交 于点F,连接 .
(1)、k= , b=;(2)、求点D的坐标;(3)、若将△ODC绕点O逆时针旋转,得到△OD′C′,其中点D′落在x轴负半轴上,判断点C′是否落在函数 (x<0)的图像上,并说明理由.25. 如图,在平行四边形 中, 是对角线, ,以点A为圆心,以 的长为半径作 ,交 边于点E,交 于点F,连接 .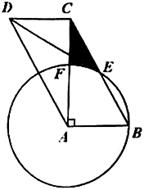 (1)、求证: 与 相切;(2)、若 , ,求阴影部分的面积.26. 在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.
(1)、求证: 与 相切;(2)、若 , ,求阴影部分的面积.26. 在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.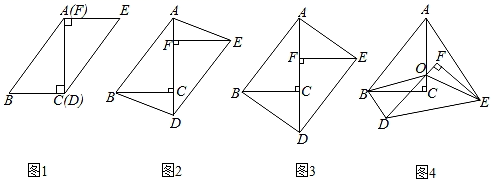 (1)、活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
(1)、活动一:将图1中的纸片DEF沿AC方向平移,连结AE,BD(如图2),当点F与点C重合时停止平移.
(思考)图2中的四边形ABDE是平行四边形吗?请说明理由.(2)、(发现)当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3).求AF的长.(3)、活动二:在图3中,取AD的中点O,再将纸片DEF绕点O顺时针方向旋转α度(0≤α≤90),连结OB,OE(如图4).
(探究)当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.27. 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.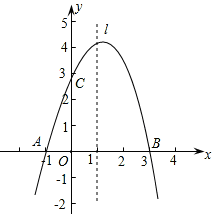 (1)、求抛物线的函数关系式;(2)、设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;(3)、在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.28. 已知抛物线y=x2+bx+c的顶点为P , 与y轴交于点A , 与直线OP交于点B .
(1)、求抛物线的函数关系式;(2)、设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标;(3)、在直线l上是否存在点M,使△MAC为等腰三角形?若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.28. 已知抛物线y=x2+bx+c的顶点为P , 与y轴交于点A , 与直线OP交于点B .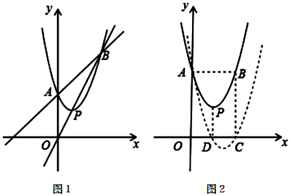 (1)、如图1,若点P的横坐标为1,点B的坐标为(3,6),①试确定抛物线的解析式;②若当m≤x≤3时,y=x2+bx+c的最小值为2,最大值为6,求m的取值范围;(2)、在(1)的条件下,若M点是直线AB下方抛物线上的一点,且S△ABM≥3,求M点横坐标的取值范围;(3)、如图2,若点P在第一象限,且PA=PO , 过点P作PD⊥x轴于点D , 将抛物线y=x2+bx+c平移,平移后的抛物线经过点 A、D , 与x轴的另一个交点为C , 试探究四边形OABC的形状,并说明理由.
(1)、如图1,若点P的横坐标为1,点B的坐标为(3,6),①试确定抛物线的解析式;②若当m≤x≤3时,y=x2+bx+c的最小值为2,最大值为6,求m的取值范围;(2)、在(1)的条件下,若M点是直线AB下方抛物线上的一点,且S△ABM≥3,求M点横坐标的取值范围;(3)、如图2,若点P在第一象限,且PA=PO , 过点P作PD⊥x轴于点D , 将抛物线y=x2+bx+c平移,平移后的抛物线经过点 A、D , 与x轴的另一个交点为C , 试探究四边形OABC的形状,并说明理由.