山东省滕州市2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 下列运算正确的是( )A、 B、 C、 D、2. 如图,已知 ,则∠BCE的度数为( )
 A、70° B、65° C、35° D、55°3. 已知 ,则 的值是( )A、 B、 C、 D、4. 下列各数中,不是不等式 的解的是( )A、-3 B、 C、 D、25. 2020年中央财政下达义务教育补助经费1695.9亿元,比上年增长8.3%.其中1695.9亿元用科学记数法表示为( )A、 元 B、 元 C、 元 D、 元6. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A、70° B、65° C、35° D、55°3. 已知 ,则 的值是( )A、 B、 C、 D、4. 下列各数中,不是不等式 的解的是( )A、-3 B、 C、 D、25. 2020年中央财政下达义务教育补助经费1695.9亿元,比上年增长8.3%.其中1695.9亿元用科学记数法表示为( )A、 元 B、 元 C、 元 D、 元6. 如图,小明想要测量学校操场上旗杆 的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角 ;(2)量得测角仪的高度 ;(3)量得测角仪到旗杆的水平距离 .利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )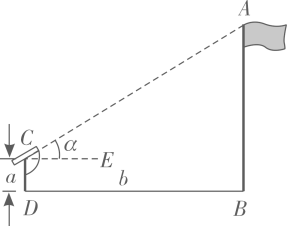 A、 B、 C、 D、7. 一个不透明的袋子中装有1个红球,2个绿球,除颜色外无其他差别,从中随机摸出一个球,然后放回摇匀,再随机摸出一个.给出下列结论:①第一次摸出的球是红球,第二次摸出的球一定是绿球;②第一次摸出的球是红球,第二次摸出的球不一定是绿球;③第一次摸出的球是红球的概率是 ;④两次摸出的球都是红球的概率是 .其中正确的结论个数为( )A、1个 B、2个 C、3个 D、4个8. 如图1,将边长为的大正方形减去一个边长为1的小正方形(阴影部分),并将剩余部分延虚线剪开,得到两个长方形,再将两个长方形拼成图2所示长方形.这两个图能解释下列哪个等式( )
A、 B、 C、 D、7. 一个不透明的袋子中装有1个红球,2个绿球,除颜色外无其他差别,从中随机摸出一个球,然后放回摇匀,再随机摸出一个.给出下列结论:①第一次摸出的球是红球,第二次摸出的球一定是绿球;②第一次摸出的球是红球,第二次摸出的球不一定是绿球;③第一次摸出的球是红球的概率是 ;④两次摸出的球都是红球的概率是 .其中正确的结论个数为( )A、1个 B、2个 C、3个 D、4个8. 如图1,将边长为的大正方形减去一个边长为1的小正方形(阴影部分),并将剩余部分延虚线剪开,得到两个长方形,再将两个长方形拼成图2所示长方形.这两个图能解释下列哪个等式( )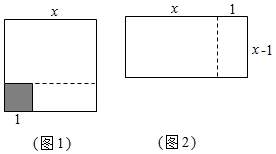 A、 B、 C、 D、9. 如图 是 切线,点A为切点, 交 于点C , 点D在 上,连接 ,若 ,则 的度数为( )
A、 B、 C、 D、9. 如图 是 切线,点A为切点, 交 于点C , 点D在 上,连接 ,若 ,则 的度数为( ) A、 B、 C、 D、10. 如图,点 在 上, ,垂足为E.若 , ,则 ( )
A、 B、 C、 D、10. 如图,点 在 上, ,垂足为E.若 , ,则 ( ) A、2 B、4 C、 D、11. 如图,在平面直角坐标系中,函数 与 的图像交于点 ,则代数式 的值为( )
A、2 B、4 C、 D、11. 如图,在平面直角坐标系中,函数 与 的图像交于点 ,则代数式 的值为( )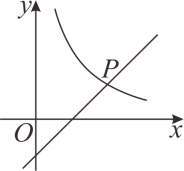 A、 B、 C、 D、12. 如图是二次函数 图象的一部分,对称轴为 ,且经过点 ,有下列说法:① ;② ;③ ;④若 是抛物线上的两点,则 ,上述说法正确的是( )
A、 B、 C、 D、12. 如图是二次函数 图象的一部分,对称轴为 ,且经过点 ,有下列说法:① ;② ;③ ;④若 是抛物线上的两点,则 ,上述说法正确的是( ) A、①②④ B、③④ C、①③④ D、①②
A、①②④ B、③④ C、①③④ D、①②二、填空题
-
13. 分解因式: = .14. 计算: = .15. 如图,在正方形网格中,每个小正方形的边长均为1,△ABC和△DEF的顶点都在网格线的交点上.设△ABC的周长为C1 , △DEF的周长为C2 , 则 的值等于.
 16. 观察下面的变化规律: 根据以上的规律计算: .17. 如图,点A再反比例函数 的图象上,点B在x轴的负半轴上,直线AB交y轴于点C , 若 ,△AOB的面积为9,则k的值为 .
16. 观察下面的变化规律: 根据以上的规律计算: .17. 如图,点A再反比例函数 的图象上,点B在x轴的负半轴上,直线AB交y轴于点C , 若 ,△AOB的面积为9,则k的值为 . 18. 如图,在 中, . 的半径为2,点 是 边上的动点,过点P作 的一条切线 (点Q为切点),则线段 长的最小值为 .
18. 如图,在 中, . 的半径为2,点 是 边上的动点,过点P作 的一条切线 (点Q为切点),则线段 长的最小值为 .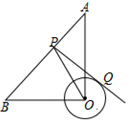
三、解答题
-
19. 先化简,再求值: ,然后从 ,0,1中选择适当的数代入求值.20. 某高速公路管理部门工作人员在对某段高速公路进行安全巡检过程中,发现该高速公路旁的一斜坡存在落石隐患.该斜坡横断面示意图如图所示,水平线 ,点A、B分别在 、 上,斜坡AB的长为18米,过点B作 于点C,且线段AC的长为 米.
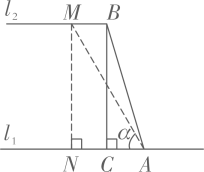 (1)、求该斜坡的坡高BC;(结果用最简根式表示)(2)、为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡脚 为60°,过点M作 于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?21. 某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:
(1)、求该斜坡的坡高BC;(结果用最简根式表示)(2)、为降低落石风险,该管理部门计划对该斜坡进行改造,改造后的斜坡坡脚 为60°,过点M作 于点N,求改造后的斜坡长度比改造前的斜坡长度增加了多少米?21. 某超市经销一种商品,每千克成本为50元,经试销发现,该种商品的每天销售量y(千克)与销售单价x(元/千克)满足一次函数关系,其每天销售单价,销售量的四组对应值如下表所示:销售单价x(元/千克)
55
60
65
70
销售量y(千克)
70
60
50
40
(1)、求y(千克)与x(元/千克)之间的函数表达式;(2)、为保证某天获得600元的销售利润,则该天的销售单价应定为多少?(3)、当销售单价定为多少时,才能使当天的销售利润最大?最大利润是多少?22. 在矩形ABCD中,E为DC边上一点,把 沿AE翻折,使点D恰好落在BC边上的点F .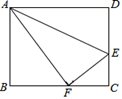 (1)、求证: ;(2)、若AB=2 ,AD=4,求EC的长.23. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象相交于 ,B两点.
(1)、求证: ;(2)、若AB=2 ,AD=4,求EC的长.23. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象相交于 ,B两点.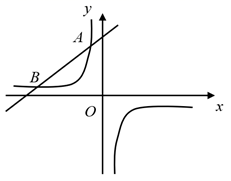 (1)、求反比例函数的表达式;(2)、将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求b的值.
(1)、求反比例函数的表达式;(2)、将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求b的值.