山东省济南市天桥区2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
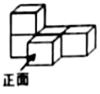
1. 3的相反数是( )A、 3 B、-3 C、 D、2. 如图是由几个相同的小正方体搭成的几何体,这个几何体的左视图是( )
 A、
A、 B、
B、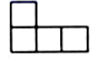 C、
C、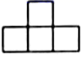 D、
D、 3. 我国实施精准扶贫政策以来,收效显著 . 据统计截至2020年底约有93000000人脱贫,93000000用科学记数法表示,正确的是( )A、 B、 C、 D、4.
3. 我国实施精准扶贫政策以来,收效显著 . 据统计截至2020年底约有93000000人脱贫,93000000用科学记数法表示,正确的是( )A、 B、 C、 D、4.如图,AB∥CD,AC⊥BC,∠BAC=65°,则∠BCD的度数等于( )
 A、20° B、25° C、35° D、50°5. 下列垃圾分类标志分别是厨余垃圾、有害垃圾、其他垃圾和可回收物,其中既是轴对称图形又是中心对称图形的是( )A、
A、20° B、25° C、35° D、50°5. 下列垃圾分类标志分别是厨余垃圾、有害垃圾、其他垃圾和可回收物,其中既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 下列运算正确的是( )A、 B、 C、 D、7. “学雷锋”活动月中,“飞翼”班将组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )A、 B、 C、 D、8. 如图是某班去年 月份全班同学每月的课外阅读数量折线统计图,下列说法正确的是( )
6. 下列运算正确的是( )A、 B、 C、 D、7. “学雷锋”活动月中,“飞翼”班将组织学生开展志愿者服务活动,小晴和小霞从“图书馆,博物馆,科技馆”三个场馆中随机选择一个参加活动,两人恰好选择同一场馆的概率是( )A、 B、 C、 D、8. 如图是某班去年 月份全班同学每月的课外阅读数量折线统计图,下列说法正确的是( ) A、每月阅读数量的众数是42 B、每月阅读数量的中位数是58 C、每月阅读数量的平均数是58 D、每月阅读数量的极差是659. 一次函数 且y随x的增大而增大,则其图象可能是( )A、
A、每月阅读数量的众数是42 B、每月阅读数量的中位数是58 C、每月阅读数量的平均数是58 D、每月阅读数量的极差是659. 一次函数 且y随x的增大而增大,则其图象可能是( )A、 B、
B、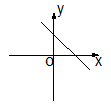 C、
C、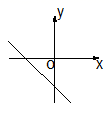 D、
D、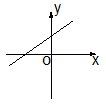 10. 如图, 的斜边 在 轴上, ,将 绕原点顺时针旋转 ,则 的对应点 的坐标为( )
10. 如图, 的斜边 在 轴上, ,将 绕原点顺时针旋转 ,则 的对应点 的坐标为( )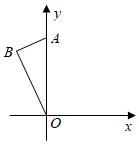 A、 B、 C、 D、11. 如图1是一个手机的支架,由底座、连杆和托架组成(连杆 始终在同一平面内), 垂直于底座且长度为 的长度为 的长度可以伸缩调整 . 如图2, 保持不变,转动 ,使得 ,假如 时为最佳视线状态,则此时 的长度为(参考数据: )( )
A、 B、 C、 D、11. 如图1是一个手机的支架,由底座、连杆和托架组成(连杆 始终在同一平面内), 垂直于底座且长度为 的长度为 的长度可以伸缩调整 . 如图2, 保持不变,转动 ,使得 ,假如 时为最佳视线状态,则此时 的长度为(参考数据: )( ) A、 B、 C、 D、12. 如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x= ,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
A、 B、 C、 D、12. 如图,抛物线y=ax2+bx+4交y轴于点A,交过点A且平行于x轴的直线于另一点B,交x轴于C,D两点(点C在点D右边),对称轴为直线x= ,连接AC,AD,BC.若点B关于直线AC的对称点恰好落在线段OC上,下列结论中错误的是( )
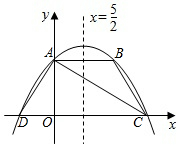 A、点B坐标为(5,4) B、AB=AD C、a= D、OC•OD=16
A、点B坐标为(5,4) B、AB=AD C、a= D、OC•OD=16二、填空题
-
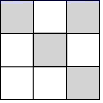
13. 分解因式: .14. 一个小球在如图所示的地板上自由滚动,并随机停在某块方砖上 . 如果每一块方砖除颜色外完全相同,那么小球最终停留在黑砖上的概率是 .
 15. 一个n边形的内角和为1080°,则n= .16. 若代数式 的值是 ,则 .17. 如图,菱形 的边长为2,点 在以点A为圆心, 为半径的圆弧上,则图中阴影部分的面积是 .
15. 一个n边形的内角和为1080°,则n= .16. 若代数式 的值是 ,则 .17. 如图,菱形 的边长为2,点 在以点A为圆心, 为半径的圆弧上,则图中阴影部分的面积是 .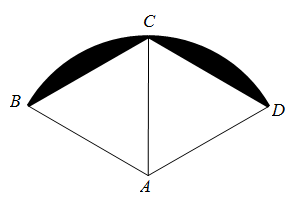 18. 如图,四边形 是矩形纸片, ,对折矩形纸片 ,使 与 重合,折痕为 ,展平后再过点B折叠矩形纸片,使点A落在 上的点N处,折痕 与 相交于点Q;再次展平,连接 ,延长 交 于点G;P为线段 上一动点 . 有如下结论:① ;② ;③ 是等边三角形;④ ;⑤H是 的中点,则 的最小值是 . 其中正确结论的序号是 .
18. 如图,四边形 是矩形纸片, ,对折矩形纸片 ,使 与 重合,折痕为 ,展平后再过点B折叠矩形纸片,使点A落在 上的点N处,折痕 与 相交于点Q;再次展平,连接 ,延长 交 于点G;P为线段 上一动点 . 有如下结论:① ;② ;③ 是等边三角形;④ ;⑤H是 的中点,则 的最小值是 . 其中正确结论的序号是 .
三、解答题
-
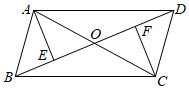
19. 计算:20. 解不等式组 ,并写出它的所有整数解 .21. 如图,在 中,对角线 与 相交于点O,点 分别为 的中点,连接 . 求证: .
 22. 在创客教育理念的指引下,国内很多学校都纷纷建立创客实践室及创客空间,致力于从小培养孩子的创新精神和创造能力,我区某校开设了 “ ”打印; 数学编程; 智能机器人; 陶艺制作,共四门创客课程 . 为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机抽样调查,他们将调查结果整理后绘制成如下三幅均不完整的统计图表 .
22. 在创客教育理念的指引下,国内很多学校都纷纷建立创客实践室及创客空间,致力于从小培养孩子的创新精神和创造能力,我区某校开设了 “ ”打印; 数学编程; 智能机器人; 陶艺制作,共四门创客课程 . 为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机抽样调查,他们将调查结果整理后绘制成如下三幅均不完整的统计图表 .最喜爱的创客课程统计表
创客课程
频数
频率
A
36
0.45
B
0.25
C
16
b
D
8
合计
a
1

请根据图表中提供的信息回答下列问题:
(1)、统计表中 ; ;(2)、图1中“D”对应扇形的圆心角为度;(3)、请补全图1中“B”所对应的条形图;(4)、若该校有2000名学生,请你根据调查估计全校最喜欢“数学编程”创客课程的人数 .23. 如图, 是 的直径,点P在 的延长线上, 切 于点 ,垂足为D,连接 . (1)、求证: ;(2)、若 ,求 的半径 .24. 某学校为了满足疫情防控需求,决定购进 两种型号的口罩若干盒 . 若购进A型口罩10盒,B型口罩5盒,共需1000元:若购进A型口罩4盒,B型口罩3盒,共需550元 .(1)、求 两种型号的口罩每盒各需多少元?(2)、若该学校决定购进这两种型号的口罩共计200盒,并要求购进A型口罩的盒数不超过B型口罩盒数的4倍,请为该学校设计出最省钱的购买方案,并说明理由 .25. 如图1,已知一次函数 的图象分别与x轴和y轴交于点A、点B,与反比例函数 的图象相交于点 .
(1)、求证: ;(2)、若 ,求 的半径 .24. 某学校为了满足疫情防控需求,决定购进 两种型号的口罩若干盒 . 若购进A型口罩10盒,B型口罩5盒,共需1000元:若购进A型口罩4盒,B型口罩3盒,共需550元 .(1)、求 两种型号的口罩每盒各需多少元?(2)、若该学校决定购进这两种型号的口罩共计200盒,并要求购进A型口罩的盒数不超过B型口罩盒数的4倍,请为该学校设计出最省钱的购买方案,并说明理由 .25. 如图1,已知一次函数 的图象分别与x轴和y轴交于点A、点B,与反比例函数 的图象相交于点 . (1)、求点C的坐标和反比例函数 的表达式;(2)、如图2,点M为线段 的中点,将线段 向左平移 个单位后,点C和点M的对应点 和 都落在另一个反比例函数 的图象上 .
(1)、求点C的坐标和反比例函数 的表达式;(2)、如图2,点M为线段 的中点,将线段 向左平移 个单位后,点C和点M的对应点 和 都落在另一个反比例函数 的图象上 .①求点M的坐标及n的值;
②连接 ,求四边形 的面积 .
26. 如图1,已知 和 均为等腰直角三角形,点 分别在线段 上,且 . (1)、观察猜想:如图2,将 绕点A逆时针旋转,连接 的延长线交 于点F . 当 的延长线恰好经过点E时,点E与点F重合,此时,
(1)、观察猜想:如图2,将 绕点A逆时针旋转,连接 的延长线交 于点F . 当 的延长线恰好经过点E时,点E与点F重合,此时,① 的值为;
② 的度数为度;
(2)、类比探究:如图3,继续旋转 ,点F与点E不重合时,上述结论是否仍然成立,请说明理由 .(3)、拓展延伸:若 ,当 所在的直线垂直于 时,请你直接写出线段 的长 .27. 如图,抛物线 的图象经过点 ,交 轴于点 和B,连接 ,直线 与 轴交于点D,与 上方的抛物线交于点E,与 交于点F . (1)、求抛物线的表达式及点B的坐标;(2)、求 的最大值及此时点E的坐标;(3)、在(2)的条件下,若点M为直线 上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点 为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由 .
(1)、求抛物线的表达式及点B的坐标;(2)、求 的最大值及此时点E的坐标;(3)、在(2)的条件下,若点M为直线 上一点,点N为平面直角坐标系内一点,是否存在这样的点M和点N,使得以点 为顶点的四边形是菱形?若存在,直接写出点M的坐标;若不存在,请说明理由 .