山东省德州市临邑武城禹城县联考2021年中考数学一模试卷

试卷更新日期：2021-05-14 类型：中考模拟

进入出卷网下载

一、单选题

1. （）的相反数的倒数是 $- \frac{1}{2021}$

A、2021 B、-2021 C、 $\pm \frac{1}{2021}$ D、 $\pm 2021$

查看试题解析
2. 在图形：（1）线段；（2）等边三角形；（3）矩形；（4）菱形；（5）平行四边形，（6）圆形中，既是轴对称图形又是中心对称图形的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
3. 如图是一个零件的示意图，它的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）

A、 ${(2 a^{2})}^{3} = 6 a^{6}$ B、 $a^{3} \cdot a^{2} = a^{5}$ C、 $2 a^{2} + 4 a^{2} = 6 a^{4}$ D、 ${(a + 2 b)}^{2} = a^{2} + 4 b^{2}$

查看试题解析
5. 已知方程组 ${\begin{array}{l} 2 x + y = 4 \\ x + 2 y = 5 \end{array}$ ，则 $x^{2} - y^{2}$ 的值为（）

A、-1 B、0 C、2 D、-3

查看试题解析
6. 如图，直线a∥b，Rt△ABC的直角顶点A落在直线a上，点B落在直线b上，若∠1＝15°，∠2＝25°，则∠ABC的大小为（）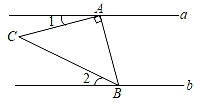

A、40° B、45° C、50° D、55°

查看试题解析
7. 若关于x的方程 $\frac{x}{x - 3} = 2 + \frac{m}{x - 3}$ 无解，则m的值是（）

A、-3 B、3 C、2 D、-2

查看试题解析
8. 计算 $\frac{a^{2}}{a - 1} - a - 1$ 的正确结果是（）

A、 $- \frac{1}{a - 1}$ B、 $\frac{1}{a - 1}$ C、 $- \frac{2 a - 1}{a - 1}$ D、 $\frac{2 a - 1}{a - 1}$

查看试题解析
9. 融侨半岛某文具店购入一批笔袋进行销售，进价为每个20元，当售价为每个50元时，每星期可以卖出100个，现需降价处理：售价每降价3元，每星期可以多卖出15个，店里每星期笔袋的利润要达到3125元．若设店主把每个笔袋售价降低x元，则可列方程为（）

A、（30+x）（100－15x）=3125 B、（30﹣x）（100+15x）=3125 C、（30+x）（100－5x）=3125 D、（30﹣x）（100+5x）=3125

查看试题解析
10. 我国魏晋时期的数学家刘徽将勾股形（古人称直角三角形为勾股形）分割成一个正方形和两对全等的直角三角形，得到一个恒等式.后人借助这种分割方法所得的图形证明了勾股定理，如图，若 $a = 2$ ， $b = 3$ ，现随机向该图形内掷一枚小针，则针尖落在阴影区域内的概率（）．

A、 $\frac{2}{5}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
11. 二次函数y=ax2+bx+c（a≠0）的部分图象如图，图象过点（-1，0），对称轴为直线x=2，下列结论：①4a+b=0；②9a+c＞3b；③8a+7b+2c＞0；④当x＞-1时，y的值随x值的增大而增大.其中正确的结论有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
12. 不等式组 ${\begin{matrix} 2 x + \frac{1}{2} > \frac{1}{2} x - 4 \\ \frac{3}{2} x - \frac{1}{2} \leq x \end{matrix}$ 的解集在数轴上表示正确的是（　　）

A、 B、 C、 D、

查看试题解析

二、填空题

13. 中国高铁近年来迅速发展．高铁技术不断走出国门，成为展示我国实力的新名片．现在中国高速铁路营运里程将达到37900公里，将37900用科学记数法表示应为．

查看试题解析
14. 对于有理数a，b定义运算※如下：a※b=(a+b)a-b，则（-3）※4=。

查看试题解析
15. 如图，在4 x 4的正方形方格图形中，小正方形的顶点称为格点，△ABC的顶点都在格点上，则图中cos∠ABC= ．

查看试题解析
16. 在平面直角坐标系中，四边形 $O A B C$ 是菱形， $∠ B = 60 °$ ，反比例函数 $y = \frac{k}{x} (k > 0)$ 的图象经过点C，若将菱形向下平移2个单位，点B恰好落在反比例函数的图象上，则反比例函数的表达式为．

查看试题解析
17. 如图， $A B$ 是⊙O的直径， $A B = 4$ ，过点B作 $⊙ O$ 的切线，C是切线上一点，且 $B C = 2$ ，P是线段 $O A$ 的中点，连接 $P C$ 交⊙O于点D，过点P作 $P C$ 的垂线，交切线 $B C$ 于点E，交⊙O于点F，则 $P E$ 的长为．

查看试题解析
18. 若函数y=mx² +（m+2）x+ $\frac{1}{2}$ m+1的图象与 x 轴只有一个交点，那么m的值为．

查看试题解析

三、解答题

19. 先化简后求值： $\frac{(16 - a^{2})}{(a^{2} + 8 a + 16)} \div \frac{(a - 4)}{2 a + 8} \cdot \frac{a - 2}{a + 2} + 2$ ，其中 $a = 2 \sin 45 ° - {(\frac{1}{2})}^{- 1}$ ．

查看试题解析
20. 为落实德州市关于开展中小学课后服务工作的要求，某学校开展了四门校本课程供学生选择：A．趣味数学；B．博乐阅读；C．快乐英语；D．硬笔书法．全校共有100名学生选择了A课程，为了解选A课程学生的学习情况，从这100名学生中随机抽取了30名学生进行测试，将他们的成绩（百分制）绘制成如下频数分布直方图．

(1)、其中 $70 \leq x < 80$ 这一组的数据为74，73，74，75，76，76，79，则这组数据的中位数是，众数是．

(2)、根据题中信息，估计该校共有人，选A课程学生成绩在 $80 \leq x < 90$ 的有人．

(3)、课程D在扇形统计图中所对应的圆心角的度数为．

(4)、如果学校规定每名学生要选两门不同的课程，小张和小王在选课程中，若第一次都选了课程C，那么他俩第二次同时选课程A或B的概率是多少？请用列表法或画树状图的方法加以说明．

查看试题解析
21. 若在方格（每小格正方形边长为 $1m$ ）上沿着网格线平移，规定：沿水平方向平移的数量为a（向右为正，向左为负，平移 $| a |$ 单位），沿竖直方向平移的数量为b（向上为正，向下为负，平移 $| b |$ 个单位），则把有序数对 ${a ， b}$ 叫做这一平移的“平移量”．例如：点A按“平移量” ${1 ， 4}$ 可平移至点B．

(1)、从点C按“平移量”{ ， }可平移到点B；

(2)、若点B依次按“平移量” ${2 ， - 2}$ ， ${- 3 ， 2}$ 平移至点D
①请在图中标出点D；（用黑色水笔在答题卡上作出点D）

②如果每平移 $1m$ 需要2.5秒，那么按此方法从点B移动至点D需要多少秒？

③观察点D的位置，其实点B也可按“平移量”{ ▲ ， ▲ }直接平移至点D；观察这两种平移的“平移量”，猜想：点依次按“平移量” ${2 ， 3}$ 、 ${- 5 ， 1}$ 、 ${1 ， - 5}$ 平移至点F，则相当于点E按“平移量”{ ▲ ， ▲ }直接平移至点F．

查看试题解析
22. 如图，在Rt $△ A B C$ 中， $∠ A C B = 90 °$ ，以斜边 $A B$ 上的中线 $C D$ 为直径作⊙O ，与 $B C$ 交于点M，与 $A B$ 的另一个交点为E，过点M作⊙O的切线 $M N$ 交 $A B$ 于点N．

(1)、求证： $M N ⊥ A B$ ；

(2)、若⊙O的直径为5， $\sin B = \frac{3}{5}$ ，求 $E D$ 的长．

查看试题解析

23. 某公司销售一种进价为

20

元/个的计算器，其销售量y（万个）与销售价格x（元/个）的变化如表：

价格x（元/个）	…	$30$	$40$	$50$	$60$	…
销售量y（万个）	…	$5$	$4$	$3$	$2$	…

同时，销售过程中的其他开支（不含进价）总计 $40$ 万元．

(1)、观察并分析表中的y与x之间的对应关系，用学过的一次函数的有关知识写出y（万个）与x（元/个）的函数解析式；

(2)、求得该公司销售这种计算器的净得利润z（万元）与销售价格x（元/个）的函数解析式，销售价格定为多少元时净得利润最大，最大值是多少？

(3)、该公司要求净得利润不能低于40万元，请写出销售价格x（元/个）的取值范围，若还需考虑销售量尽可能大，销售价格应定为多少元？

查看试题解析

24. 在正方形 $A B C D$ 中，E是 $C D$ 边上任意一点，连接 $A E$ ．将 $A E$ 绕点A顺时针旋转 $45 °$ ， $A E$ 所在的直线与 $B C$ 交与点F，连接 $E F$ ．

(1)、探究：以A为圆心， $A E$ 为半径作圆，交 $C B$ 的延长线于点G，连接 $A G$ （如图1）．求证： $B F + D E = E F$ ；

(2)、应用：点E在 $D C$ 边上移动，当 $E C = C F$ 时，直线 $E F$ 与 $A B$ 、 $A D$ 的延长线分别交于点M、N．（如图2）．求证： $E F^{2} = M F^{2} + N E^{2}$ ；

(3)、类比：将正方形改为长与宽不相等的矩形，在（2）的条件下，其余条件不变（如图3），直接写出线段 $E F$ 、 $B F$ 、 $D E$ 之间的数量关系．

查看试题解析
25. 如图，在平面直角坐标系中点M的坐标是 $(5 ， 4)$ ，⊙M与x轴相交于A、B两点，与y轴相切于点C，抛物线 $y = a x^{2} + b x + c$ 经过A、B、C三点．

(1)、求抛物线的解析式；

(2)、设抛物线的顶点为D．求证：直线 $A D$ 与⊙M相切；

(3)、在（2）的条件下，设直线 $A D$ 与y轴交于点F，点P是抛物线上一动点，过点P作y轴的平行线与直线 $A D$ 相交于点Q，若点Q关于直线 $P F$ 的对称点恰好落在y轴上，直接写出P点的横坐标．

查看试题解析