内蒙古自治区呼和浩特市2021年中考数学一模试卷

试卷更新日期：2021-05-14 类型：中考模拟

进入出卷网下载

一、单选题

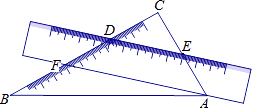
1. 高度每增加1 km，气温大约下降6 ℃，现在地面温度是25 ℃，某飞机在该地上空6 km处，则此时飞机所在高度的气温为（　　）

A、-9 ℃ B、-11 ℃ C、9 ℃ D、11 ℃

查看试题解析
2. 将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置，如果∠CDE=40°，那么∠BAF的大小为（）

A、10° B、15° C、20° D、25°

查看试题解析
3. 在一条笔直的航道上依次有甲、乙、丙三个港口，一艘船从甲港出发，沿直线匀速行驶经过乙港驶向丙港，最终到达丙港，设行驶x（h）后，与乙港的距离为y（km），y与x的函数关系如图所示，则下列说法错误的是（　　）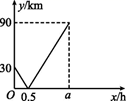

A、乙港与丙港的距离是90 km B、船在中途休息了0.5 h C、船的行驶速度是60 km/h D、从乙港到达丙港共花了1.5 h

查看试题解析
4. 小王第一天做了x个零件，第二天比第一天多做5个，第三天做的零件是第二天的2倍，若三天共做零件75个，则第一天做了（　　）

A、15个 B、14个 C、10个 D、20个

查看试题解析
5. 某班学生做“用频率估计概率”的实验时，给出的某一结果出现如图所示的统计图，则符合这一结果的实验可能是（　　）

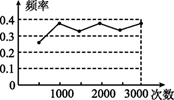A、抛一枚硬币，出现正面朝上 B、从标有1，2，3，4，5，6的六张卡片中任抽一张，出现偶数 C、从一个装有6个红球和3个黑球的袋子中任取一球，取到的是黑球 D、先后两次掷一枚质地均匀的正六面体骰子，两次向上的点数之和是7

查看试题解析
6. 我国古代数学家刘徽创立的“割圆术”可以估算圆周率π，理论上能把π的值计算到任意精度．祖冲之继承并发展了“割圆术”，将π的值精确到小数点后第七位，这一结果领先世界一千多年，“割圆术”的第一步是计算半径为1的圆内接正六边形的面积S₆ ，则S₆的值为（　　）

A、 $ \sqrt{3}$ B、2 $ \sqrt{3}$ C、 $\frac{3 \sqrt{3}}{2}$ D、 $ \frac{2}{3} \sqrt{3}$

查看试题解析
7. 某几何体的三视图如图所示；则该几何体的表面积为（　　）

A、6 $\sqrt{3}$ +6+2 $\sqrt{2}$ B、18+2 $\sqrt{2}$ C、3 $\sqrt{2}$ D、6 $\sqrt{2}$

查看试题解析
8. 已知 $x_{1}$ ， $x_{2}$ 是方程2 $x^{2}$ +2x-3=0的两个根，则 $\frac{2}{x_{1}^{2} - 1} - \frac{1}{x_{1}^{2} + x_{2} + 1}$ 的值为（　　）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、1 D、 $\frac{4}{3}$

查看试题解析
9. 如图，矩形ABCD中，AB：AD=2：1，E为AB的中点，F为EC上一动点，P为DF中点，连接PB ，当PB的最小值为3 $\sqrt{2}$ 时，AD的值为（　　）

A、2 B、3 C、4 D、6

查看试题解析
10. 给出以下四个命题：
①以现价销售一件商品的利润率为30%，如果商家在现在价格的基础上先提价40%，后降价50%进行销售，商家还能有利润；

②数据x₁ ， x₂ ， x₃ ， x₄的方差是3，则数据x₁+1，x₂+1，x₃+1，x₄+1的方差还是3；

③若圆锥的侧面展开图是一个半圆，则母线AB与高AO的夹角为30°；

④已知关于a的一次函数y=2ax²+2x-3(x≠0)在-1≤a≤1上函数值恒小于零，则实数x的取值范围为- $\frac{1}{2}$ - $\frac{\sqrt{7}}{2}$ <x<0或0<x<- $\frac{1}{2}$ + $\frac{\sqrt{7}}{2}$ ．

其中正确命题的个数为（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

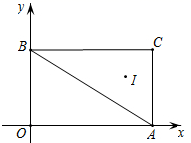
11. 2019年第一季度，我国国民经济开局平稳，积极因素逐渐增多．社会消费品零售总额约为97790亿元，同比增长8.3%；网上零售额为22379亿元，同比增长15.3% ．其中22379亿用科学记数法表示为．

查看试题解析
12. 已知直线y=kx+b与两坐标轴的交点都在正半轴上，则|k-b|- $\sqrt{k^{2}}$ = ．

查看试题解析
13. 在正方形ABCD中，点E ， F分别为BC和AB的中点，DE和FC交于点M ，连接AM ．若BC=5，则AM的长度为．

查看试题解析
14. 已知关于x的不等式 $\frac{2 m - m x}{2}$ > $\frac{1}{2}$ x-1，当m=1时，该不等式的解集为；若该不等式的解集中的每一个x都能使关于x的不等式x>a成立，则此时m的取值范围为， a的取值范围是．

查看试题解析
15. 如图，在平面直角坐标系xOy中，A（4，0），B（0，3），C（4，3），点I是△ABC的内心，则点I的坐标为；点I关于原点对称的点的坐标为．

查看试题解析
16. 在平面直角坐标系xOy中，抛物线y=-x²+6x-8与x轴交于点A ， B（点A在点B的左侧），与y轴交于点C ．垂直于y轴的直线l与抛物线交于点P（x₁ ， y₁），Q（x₂ ， y₂），与直线BC交于点N（x₃ ， y₃），若x₁<x₂<x₃ ，记s=x₁+x₂+x₃ ，则s的取值范围为．

查看试题解析

三、解答题

17.

(1)、计算：2 $\sqrt{6}$ ·sin60°-|7-5 $\sqrt{2}$ |+2÷ $（ \sqrt{2} ）$ ^-¹ ．

(2)、解方程： $\frac{3}{x}$ - $\frac{2 x}{x + 1}$ =-2 ．

查看试题解析
18. 如图，四边形ABCD中，∠B=60°，AC=BC ，点E在AB上，将CE绕点C顺时针旋转60°得CF ，且点F在AD上．

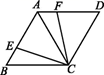(1)、求证：AF=BE；

(2)、若AE=DF ，求证：四边形ABCD是菱形；

(3)、若BC=2 $\sqrt{3}$ ，求四边形AFCE的面积．

查看试题解析
19. 在塔前平地上选取一点A作为观测点竖立一根长1.6米的测杆AD ，观测塔顶N的仰角为45°，将测杆AD向塔的方向平移8米到达BC位置，此时观测塔顶N的仰角为65°，计算塔的高度MN（用含有非特殊角的三角函数表示结果）．

查看试题解析

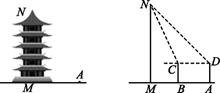20. 某区在实施居民用水额定管理前，对居民生活用水情况进行了调查，下表是通过简单随机抽样获得的50个家庭去年的月均用水量（单位：吨），并将调查数据进行了如下整理：

分组	划记	频数
2.0＜x≤3.5	正正一	11
3.5＜x≤5.0		19
5.0＜x≤6.5
6.5＜x≤8.0
8.0＜x≤9.5		2
合计		50

(1)、把上面的频数分布表和频数分布直方图补充完整；

(2)、请你用频数分布直方图计算这50个家庭去年的月均用水量的平均数和中位数（各组的实际数据用该组的组中值表示）；若该小区有2000个家庭，请你用频数分布直方图得到的数据估计该小区月均用水总量；

(3)、为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使60%的家庭收费不受影响，你觉得家庭月均用水量标准应该定为多少?为什么?

查看试题解析

21. 我们知道，任意一个正整数x都可以进行这样的分解：x=m×n（m，n是正整数，且m≤n），在x的所有这种分解中，如果m，n两因数之差的绝对值最小，我们就称m×n是x的最佳分解．并规定：f（x）= $\frac{m}{n}$ .
例如：18可以分解成1×18，2×9或3×6，因为18-1>9-2>6-3，所以3×6是18的最佳分解，所以f（18）= $\frac{3}{6}$ = $\frac{1}{2}$ ．

(1)、填空：f（6）= ， f（9）=；

(2)、一个两位正整数t（t=10a+b，1≤a≤b≤9，a，b为正整数），交换其个位上的数字与十位上的数字，得到的新数减去原数所得的差为54，求出所有满足条件的两位正整数，并求f（t）的最大值．

查看试题解析
22. 如图，在平面直角坐标系内，反比例函数y= $\frac{k}{x}$ （x>0）的图象过点A（m ， 4）和点B ，且点B的横坐标大于1，过A作x轴的垂线，垂足为C（1，0），过点B作y轴的垂线，垂足为D ，且△ABD的面积等于4．记直线AB的函数解析式为y=ax+b（a≠0）．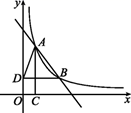

(1)、求点B的坐标；

(2)、求直线AB的函数解析式；

(3)、请直接写出 $\frac{k}{x}$ >ax+b成立时，对应的x的取值范围．

查看试题解析
23. 如图，在Rt△ABC中，∠ABC=90°，AC的垂直平分线分别与AC ， BC及AB的延长线相交于点D ， E ， F ，且BF=BC ， ⊙O是△BEF的外接圆，∠EBF的平分线交EF于点G ，交⊙O于点H ，连接BD ， FH ．

(1)、试判断BD与⊙O的位置关系，并说明理由；

(2)、若AB=1，求HG·HB的值．

查看试题解析
24. 2020年是脱贫攻坚收官之年，为贯彻落实党中央全面建成小康社会的新部署，某贫困地区的广大党员干部深入农村积极开展“精准扶贫”工作．如果将农村家庭人均年纯收入8000元作为一个标准，该地区仅剩部分家庭尚未达标.2019年7月，为估计该地区能否在2020年底达到上述标准，统计了当时该地某一贫困家庭2019年1至6月的人均月纯收入，汇总如下：

月份代码

1

2

3

4

5

6

人均月纯收（元）

310

350

390

430

470

510

根据分析，发现该家庭人均月纯收入y与月份代码x之间具有一次函数关系（记2019年1月、2月、…、2020年1月、…分别为x=1，x=2，…，x=13，…，依此类推）．

由于新冠肺炎疫情的影响，该家庭2020年第一季度每月人均月纯收入只有2019年12月人均月纯收入的三分之二．根据以上信息，完成以下问题．

(1)、求该家庭人均月纯收入y与月份代码x之间的函数关系式；

(2)、若疫情没有暴发，2020年底该家庭能否达到人均年纯收入8000元的标准?

(3)、2020年3月初开始，在当地党员干部的扶持下，该家庭的人均月纯收入y与月份代码x之间满足二次函数y=x²+bx+c的关系．若该家庭2020年12月人均月纯收入不低于1400元，求b的最小值．

(4)、若以该家庭2020年3月人均月纯收入为基数，以后每月的增长率为a ，为了使该家庭2020年底能达到人均年纯收入8000元的标准，a至少为多少?（结果保留两位小数）
（参考数据： $\sqrt{45^{2} + 4 \times 120 \times 4}$ ≈62.81）（参考公式：1+x+x²+…+x⁹= $\frac{x^{10} - 1}{x - 1}$ ；（1+a）¹⁰≈1+10a+45a²+120a³（|a|<0.15）．

查看试题解析

月份代码	1	2	3	4	5	6
人均月纯收（元）	310	350	390	430	470	510