内蒙古鄂尔多斯市2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 在 这四个数中,最小的数是( )A、0 B、 C、 D、2. 已知点A(x﹣2,3)与点B(x+4,y﹣5)关于原点对称,则yx的值是( )A、2 B、 C、4 D、83. 下列左图表示一个由相同小立方块搭成的几何体的俯视图,小正方形中的数字表示该位置上小立方块的个数,则该几何体的主视图为( )
 A、
A、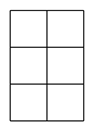 B、
B、 C、
C、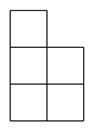 D、
D、 4. 下列计算错误的是( )A、(a3b)•(ab2)=a4b3 B、xy2- xy2= xy2 C、a5÷a2=a3 D、(-mn3)2=m2n55. 下表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
4. 下列计算错误的是( )A、(a3b)•(ab2)=a4b3 B、xy2- xy2= xy2 C、a5÷a2=a3 D、(-mn3)2=m2n55. 下表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)成绩(个/分钟)
140
160
169
170
177
180
人数
1
1
1
2
3
2
则关于这10名同学每分钟跳绳的测试成绩,下列说法正确的是( )
A、中位数是173.5 B、平均数是169.5 C、方差是135 D、众数是1706. 如图,已知直线 ,一块含30°角的直角三角板如图所示放置, ,则 等于( ) A、25° B、35° C、40° D、45°7. 尺规作图:过直线外一点作已知直线的垂线,已知:如图(1),直线 及外一点 ,求作 的垂线,使它经过点 ,小红的做法如下:
A、25° B、35° C、40° D、45°7. 尺规作图:过直线外一点作已知直线的垂线,已知:如图(1),直线 及外一点 ,求作 的垂线,使它经过点 ,小红的做法如下:①在直线 上任取一点B,连接
②以 为圆心, 长为半径作弧,交直线 于点 ;
③分别以 为圆心, 长为半径作弧,两弧相交于点 ;
④作直线 ,直线 即为所求如图(2),小红的做题依据是( )
 A、四条边都相等的四边形是菱形;菱形的对角线互相垂直 B、直径所对的圆周角是直角 C、直线外一点到这条直线上垂线段最短 D、同圆或等圆中半径相等8. 下列说法正确的有( )
A、四条边都相等的四边形是菱形;菱形的对角线互相垂直 B、直径所对的圆周角是直角 C、直线外一点到这条直线上垂线段最短 D、同圆或等圆中半径相等8. 下列说法正确的有( )①等边三角形、菱形、正方形、圆既是轴对称图形又是中心对称图形.
②九边形的内角和等于 ;
③ 的整数部分是x,小数部分是y,则
④一元二次方程 有两个不相等的实数根.
⑤对于命题“对顶角相等”,它的逆命题是假命题.
A、①②④ B、②③⑤ C、③④⑤ D、④⑤①9. 在Rt△ABC中,∠ACB=90°.AC=8,BC=3,点D是BC边上动点,连接AD交以CD为直径的圆于点E,则线段BE长度的最小值为( ) A、1 B、 C、 D、10. 如图,在矩形ABCD中, , , 一个三角形的直角顶点E是边AB上的一动点,一直角边过点D , 另一直角边与BC交于F , 若 , , 则y关于x的函数关系的图象大致为( )
A、1 B、 C、 D、10. 如图,在矩形ABCD中, , , 一个三角形的直角顶点E是边AB上的一动点,一直角边过点D , 另一直角边与BC交于F , 若 , , 则y关于x的函数关系的图象大致为( ) A、
A、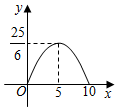 B、
B、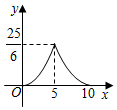 C、
C、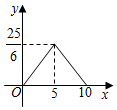 D、
D、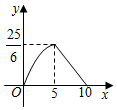
二、填空题
-
11. 若 在实数范围内有意义,则实数x的取值范围是.12. 面对突如其来的疫情,全国广大医务工作者以白衣为战袍,义无反顾的冲在抗疫战争的一线,用生命捍卫人民的安全.据统计,全国共有346支医疗队,将近42600名医护工作者加入到支援湖北武汉的抗疫队伍,将42600用科学记数法表示.13. 对实数 定义新运算 例如: ,化简 .14. 已知a、b可以取﹣2、﹣1、1、2中任意一个值(a≠b),则直线y=ax+b的图象不经过第四象限的概率是.15. 如图,在平面直角坐标系中,矩形 的顶点 分别在x轴的负半轴,y轴的正半轴上,点B在第二象限.将矩形 绕点O顺时针旋转,使点B落在y轴上,得到矩形 与 相交于点M.若经过点M的反比例函数 的图象交 于点N,矩形 的面积为8, ,则 的长为.
 16. 如图,放置的△OAB1 , △B1A1B2 , △B2A2B3 , 都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3都在直线y= x上,则点A2020的坐标为.
16. 如图,放置的△OAB1 , △B1A1B2 , △B2A2B3 , 都是边长为2的等边三角形,边AO在y轴上,点B1、B2、B3都在直线y= x上,则点A2020的坐标为.
三、解答题
-
17.(1)、先化简,再求值: ,其(2)、解不等式组: 并把解集在数轴上表示出来.18. 随着通讯技术的迅猛发展,人与人之间的沟通方式变得更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息回答下列问题:
 (1)、本次调查共调查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,请估计该校最喜欢用“微信”沟通的学生有多少名?(4)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.19. 某挖掘机的底座高AB=0.8米,动臂BC=1.2米,CD=1.5米,BC与CD的固定夹角∠BCD=140°.初始位置如图 1,斗杆顶点D 与铲斗顶点E 所在直线DE 垂直地面AM于点E,测得∠CDE=70°(示意图 2).工作时如图 3,动臂BC 会绕点B 转动,当点 A,B,C在同一直线时,斗杆顶点D 升至最高点(示意图 4).
(1)、本次调查共调查了名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、该校共有1500名学生,请估计该校最喜欢用“微信”沟通的学生有多少名?(4)、某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.19. 某挖掘机的底座高AB=0.8米,动臂BC=1.2米,CD=1.5米,BC与CD的固定夹角∠BCD=140°.初始位置如图 1,斗杆顶点D 与铲斗顶点E 所在直线DE 垂直地面AM于点E,测得∠CDE=70°(示意图 2).工作时如图 3,动臂BC 会绕点B 转动,当点 A,B,C在同一直线时,斗杆顶点D 升至最高点(示意图 4). (1)、求挖掘机在初始位置时动臂BC与AB的夹角∠ABC 的度数.(2)、问斗杆顶点D 的最高点比初始位置高了多少米(精确到 0.1米)?
(1)、求挖掘机在初始位置时动臂BC与AB的夹角∠ABC 的度数.(2)、问斗杆顶点D 的最高点比初始位置高了多少米(精确到 0.1米)?(考数据:sin50°≈0.77,cos50°≈0.64,sin70°≈0.94,cos70°≈0.34, )
20. 在抗击新型冠状病毒感染的肺炎疫情过程中,某医药研究所正在试研发一种抑制新型冠状病毒的药物,据临床观察:如果成人按规定的剂量注射这种药物,注射药物后每毫升血液中的含药量y(微克)与时间t(小时)之间的关系近似地满足图中折线.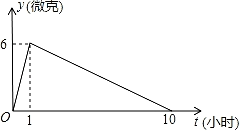 (1)、求注射药物后每毫升血液中含药量y与时间t之间的函数关系式,并写出自变量的取值范围;(2)、据临床观察:每毫升血液中含药量不少于4微克时,对控制病情是有效的.如果病人按规定的剂量注射该药物后,求控制病情的有效时间.21. 如图,在 中, , 的平分线 交 于点 ,点 在 上,以 为直径的 经过点 .
(1)、求注射药物后每毫升血液中含药量y与时间t之间的函数关系式,并写出自变量的取值范围;(2)、据临床观察:每毫升血液中含药量不少于4微克时,对控制病情是有效的.如果病人按规定的剂量注射该药物后,求控制病情的有效时间.21. 如图,在 中, , 的平分线 交 于点 ,点 在 上,以 为直径的 经过点 . (1)、求证:① 是 的切线;
(1)、求证:① 是 的切线;② ;
(2)、若点 是劣弧 的中点,且 ,试求阴影部分的面积.22. 某校为改善办学条件,计划购进 两种规格的书架,经市场调查发现有线下和线上两种方式,具有情况如下表:规格
线下
线上
单价(元/个)
运费(元/个)
单价(元/个)
运费(元/个)
A
240
0
210
20
B
300
0
250
30
(1)、如果在线下购买 两种书架20个,共花费5520元,求 两种书架各购买了多少个;(2)、如果在线上购买 两种书架20个,共花费 元,设其中 种书架购买 个,求W关于 的函数关系式;(3)、在(2)的条件下,若购买 种书架的数量不少于 种书架的2倍,请求出花费最少的购买方案,并计算按照该购买方案线上比线下节约多少钱.23. 如图,抛物线y=ax2+bx+3经过点A(﹣1,0),B(2,0)两点,与y轴交于点C,点D是抛物线上一个动点,设点D的横坐标为m(0<m<2).连接AC,BC,DB,DC. (1)、求抛物线的函数表达式;(2)、△BCD的面积何时最大?求出此时D点的坐标和最大面积;(3)、在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.24. 如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)、求抛物线的函数表达式;(2)、△BCD的面积何时最大?求出此时D点的坐标和最大面积;(3)、在(2)的条件下,若点M是x轴上一动点,点N是抛物线上一动点,试判断是否存在这样的点M,使得以点B,D,M,N为顶点的四边形是平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.24. 如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点. (1)、观察猜想:
(1)、观察猜想:图1中,线段PM与PN的数量关系是 , 位置关系是;
(2)、探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)、拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.