江西省2021年中考数学第五次联考模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. tan45°的值等于( )A、 B、 C、 D、12. 如图,这是一个由2个大小不一样的圆柱组成的几何体,则该几何体的主视图是( )
 A、
A、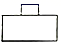 B、
B、 C、
C、 D、
D、 3. 在 中, ,则下列结论正确的是( )A、 B、 C、 D、4. 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC,若∠BCO=α,则∠P的度数为( )
3. 在 中, ,则下列结论正确的是( )A、 B、 C、 D、4. 如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC,若∠BCO=α,则∠P的度数为( ) A、2α B、90°﹣2α C、45°﹣2α D、45°+2α5. 已知关于x的方程x2+kx+2=0的两个根为x1 , x2 , 且 ,则k的值为( )A、0 B、2 C、4 D、86. 如图,在平面直角坐标系xOy中,直线l与x轴平行,且直线l分别与反比例函数 (x>0)和 (x<0)的图象交于点P和点Q . 若△POQ的面积为10,则k的值为( )
A、2α B、90°﹣2α C、45°﹣2α D、45°+2α5. 已知关于x的方程x2+kx+2=0的两个根为x1 , x2 , 且 ,则k的值为( )A、0 B、2 C、4 D、86. 如图,在平面直角坐标系xOy中,直线l与x轴平行,且直线l分别与反比例函数 (x>0)和 (x<0)的图象交于点P和点Q . 若△POQ的面积为10,则k的值为( )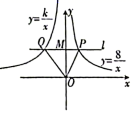 A、10 B、12 C、﹣10 D、﹣12
A、10 B、12 C、﹣10 D、﹣12二、填空题
-
7. 在反比例函数 的图象每一条曲线上,y都随x的增大而减小,则m的取值范围是 .8. 如图, ,则 .
 9. 在一个不透明的口袋中,放入标有数字1,2,2,3,4的五个小球(除数字外完全相同),从中随机摸出一个小球后放回,再随机摸出一个小球,则两次摸出的小球标号之和为5的概率为 .10. 如图,在△ABC中,AD是BC边上的高,cosC= ,AB=6 ,AC=6,则BC的长为 .
9. 在一个不透明的口袋中,放入标有数字1,2,2,3,4的五个小球(除数字外完全相同),从中随机摸出一个小球后放回,再随机摸出一个小球,则两次摸出的小球标号之和为5的概率为 .10. 如图,在△ABC中,AD是BC边上的高,cosC= ,AB=6 ,AC=6,则BC的长为 . 11. 如图,已知 的半径为2, 内接于 , ,则弓形 (阴影部分)的面积为 .
11. 如图,已知 的半径为2, 内接于 , ,则弓形 (阴影部分)的面积为 .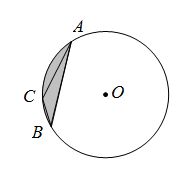 12. 定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.如图,在矩形ABCD中,AB=6,BC=9,P是对角线AC上一点,且AP:PC=2:3,过点P作直线分别交边AD , BC于点E , F , 使四边形ABFP是等腰直角四边形,则AE的长是 .
12. 定义:有一组邻边相等,并且它们的夹角是直角的凸四边形叫做等腰直角四边形.如图,在矩形ABCD中,AB=6,BC=9,P是对角线AC上一点,且AP:PC=2:3,过点P作直线分别交边AD , BC于点E , F , 使四边形ABFP是等腰直角四边形,则AE的长是 .
三、解答题
-
13.(1)、计算: ﹣2cos45°;(2)、解方程:2x2﹣5x+1=0.14. 如图,D是△ABC的BC边上一点,E为AD上一点,若∠DAC=∠B,CD=CE,试说明△ACE∽△BAD.
 15. 小贤同学总是不爱整理自己的物品,他的床头抽屉里放着3只白袜子和1双黑袜子,这些袜子除了颜色不同外没有任何区别,并且袜子在抽屉里是散开混在一起的.(1)、若小贤从抽屉里随机摸出一只袜子,则摸到白袜子的概率是 .(2)、若小贤从抽屉中随机一次性摸出两只袜子,请用列表法或画树状图法求小贤摸出的袜子恰好颜色相同的概率.16. 如图,在△ABC中,AB为半圆的直径,请仅用无刻度的直尺分别按下列要求作图(保留作图痕迹).
15. 小贤同学总是不爱整理自己的物品,他的床头抽屉里放着3只白袜子和1双黑袜子,这些袜子除了颜色不同外没有任何区别,并且袜子在抽屉里是散开混在一起的.(1)、若小贤从抽屉里随机摸出一只袜子,则摸到白袜子的概率是 .(2)、若小贤从抽屉中随机一次性摸出两只袜子,请用列表法或画树状图法求小贤摸出的袜子恰好颜色相同的概率.16. 如图,在△ABC中,AB为半圆的直径,请仅用无刻度的直尺分别按下列要求作图(保留作图痕迹). (1)、如图1,点C在半圆外,作△ABC的高CD .(2)、如图2,点C在半圆内,作△ABC的高CE .17. 如图,一次函数y=kx+b与反比例函数 (其中mk≠0)的图象交于A(﹣4,2),B(2,n)两点.
(1)、如图1,点C在半圆外,作△ABC的高CD .(2)、如图2,点C在半圆内,作△ABC的高CE .17. 如图,一次函数y=kx+b与反比例函数 (其中mk≠0)的图象交于A(﹣4,2),B(2,n)两点. (1)、求一次函数和反比例函数的表达式.(2)、请直接写出当一次函数值大于反比例函数值时x的取值范围.18. 某药研所研发了一种治疗某种疾病的新药,经测试发现:新药在人体的释放过程中,10分钟内(含10分钟),血液中含药量y(微克)与时间x(分钟)的关系满足 ;10分钟后,y与x的关系满足反比例函数 .部分实验数据如表:
(1)、求一次函数和反比例函数的表达式.(2)、请直接写出当一次函数值大于反比例函数值时x的取值范围.18. 某药研所研发了一种治疗某种疾病的新药,经测试发现:新药在人体的释放过程中,10分钟内(含10分钟),血液中含药量y(微克)与时间x(分钟)的关系满足 ;10分钟后,y与x的关系满足反比例函数 .部分实验数据如表:时间x(分钟)
…
10
15
…
含药量y(微克)
…
30
20
…
(1)、分别求当 和 时,y与x之间满足的函数关系式.(2)、据测定,当人体中每毫升血液中的含药量不低于3微克时,治疗才有效,那么该药的有效时间是多少?19. 某次台风来袭时,一棵笔直且垂直于地面的大树AB被刮倾斜7°(∠BAB′=7°)后在C处折断倒在地上,树的顶部恰好接触到地面D处(如图),测得∠ADC=37°,AD=5米. (1)、填空:∠ACD的度数为 .(2)、求这棵大树AB的高.(结果精确到0.1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ≈1.73)20. 如图,在平行四边形 中, ,过点D作 ,垂足为E , 连接 ,F为线段 上一点,且 .
(1)、填空:∠ACD的度数为 .(2)、求这棵大树AB的高.(结果精确到0.1米,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75, ≈1.73)20. 如图,在平行四边形 中, ,过点D作 ,垂足为E , 连接 ,F为线段 上一点,且 . (1)、求证: .(2)、若 ,求 的长.21. 如图,以△ABC的AC边为直径作⊙O , 交AB于点D , E是AC上一点,连接DE并延长交⊙O于点F , 连接AF , 且∠AFD=∠B .
(1)、求证: .(2)、若 ,求 的长.21. 如图,以△ABC的AC边为直径作⊙O , 交AB于点D , E是AC上一点,连接DE并延长交⊙O于点F , 连接AF , 且∠AFD=∠B . (1)、求证:BC是⊙O的切线.(2)、当AE=AD时:
(1)、求证:BC是⊙O的切线.(2)、当AE=AD时:①若∠FAC=25°,求∠B的度数;
②若OA=5,AD=6,求DE的长.
22. 在 中, ,点E在射线 上运动.连接 ,将线段 绕点E顺时针旋转 得到 ,连接 . (1)、如图1,点E在点B的左侧运动.
(1)、如图1,点E在点B的左侧运动.①当 , 时,则 ;
②猜想线段 与 之间的数量关系为 .
(2)、如图2,点E在线段 上运动时,第(1)问中线段 与 之间的数量关系是否仍然成立?如果成立,请说明理由;如果不成立,请求出它们之间新的数量关系.(3)、点E在射线 上运动, ,设 ,以A , E , C , F为顶点的四边形面积为y , 请直接写出y与x之间的函数关系式(不用写出x的取值范围).23. 如图,直线y=﹣x+n与x轴交于点A(3,0),与y轴交于点B , 抛物线y=﹣x2+bx+c经过点A , B . (1)、求抛物线的解析式.(2)、M是抛物线对称轴上的一点连接BM , CM , 求BM+CM的最小值.(3)、若E(m , 0)为x轴正半轴上一动点,过点E作直线ED⊥x轴,交直线AB于点D , 交抛物线于点P , 连接BP , BC , 当∠PBD+∠CBO=45°时,请求出m的值.
(1)、求抛物线的解析式.(2)、M是抛物线对称轴上的一点连接BM , CM , 求BM+CM的最小值.(3)、若E(m , 0)为x轴正半轴上一动点,过点E作直线ED⊥x轴,交直线AB于点D , 交抛物线于点P , 连接BP , BC , 当∠PBD+∠CBO=45°时,请求出m的值.