江西赣州经开区2021年中考数学模拟试卷

试卷更新日期：2021-05-14 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2021$ 的倒数是（）

A、2021 B、 $\frac{1}{2021}$ C、 $- 2021$ D、 $- \frac{1}{2021}$

查看试题解析
2. 下列运算正确的是（）．

A、 $2 a^{2} \cdot 3 a^{3} = 6 a^{6}$ B、 ${(a - 2)}^{2} = a^{2} - 2 a + 4$ C、 ${(- 2 a b^{2})}^{3} = - 8 a b^{6}$ D、 $(\sqrt{3} - 2) (\sqrt{3} + 2) = - 1$

查看试题解析
3. 如图是由6个相同的小正方体搭成的几何体，若去掉上层的一个小正方体，则下列说法正确的是（）．

A、主视图一定变化 B、左视图一定变化 C、俯视图一定变化 D、三种视图都不变化

查看试题解析
4. 本学期某校举行了四次数学测试，李娜同学四次的成绩（单位：分）分别为80，70，90，70，王玥同学四次的成绩分别为80， $a (a \geq 70)$ ，70，90，且李娜同学四次成绩的中位数比王玥同学四次成绩的中位数少5分，则下列说法正确的是（）．

A、a的值为70 B、两位同学成绩的平均数相同 C、李娜同学成绩的众数比王玥同学成绩的众数大 D、王玥同学的成绩比李娜同学的成绩稳定

查看试题解析
5. 将一个等腰三角形沿底边上的中线剪开，用剪下的两个三角形拼成的所有四边形中，是中心对称图形的有（）．

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 如图，在四边形 $A B C D$ 中， $∠ B = ∠ D = 90 °$ ，连接 $A C$ ， $∠ B A C = 45 °$ ， $∠ C A D = 30 °$ ， $C D = 2$ ，点P是四边形 $A B C D$ 边上的一个动点，若点P到 $A C$ 的距离为 $\sqrt{3}$ ，则点P的位置有（）．

A、4处 B、3处 C、2处 D、1处

查看试题解析

二、填空题

7. 分解因式： $a^{2} - 4 b^{2} =$ ．

查看试题解析
8. 中国网3月1日讯，国家统计局发布2020年国民经济和社会发展统计公报，初步核算，全年国内生产总值约 $101.6$ 万亿元，将数据 $101.6$ 万亿元用科学记数法表示为元．

查看试题解析
9. 已知 $x_{1}$ ， $x_{2}$ 是方程 $x^{2} + m x - 3 = 0$ 的两个实数根，且 $x_{1} = 3$ ，则 $2 m - 2 x_{1} x_{2} =$ ．

查看试题解析
10. 如图，在平面直角坐标系中，已知菱形 $O A B C$ 的顶点C在x轴上，若点A的坐标为 $(3 ， 4)$ ，经过点A的双曲线交边 $B C$ 于点D，则 $△ O A D$ 的面积为．

查看试题解析
11. 勾股定理是一个基本的几何定理，有数百种证明方法．“青朱出入图”是我国古代数学家证明勾股定理的几何证明法．刘徽描述此图“勾自乘为朱方，股自乘为青方，令出入相补，各从其类，加就其余不动也，合成弦方之幂，开方除之，即弦也”．若图中 $B F = 4$ ， $D F = 2$ ，则 $A E =$ ．

查看试题解析
12. 当 $- 2 \leq x \leq 1$ 时，二次函数 $y = - {(x - m)}^{2} + m^{2} + 1$ 有最大值4，则实数m的值为．

查看试题解析

三、解答题

13.

(1)、计算： ${(2 + \sqrt{3})}^{0} + {(- 1)}^{2021} - | \sqrt{8} - 1 |$ ；

(2)、如图，已知 $△ A B C$ ，点E在边 $A C$ 上，过点B作 $B D // A C$ ，且 $A E = B D$ ，连接 $D E$ 交 $A B$ 于点F．求证： $A F = B F$ ．

查看试题解析
14. 化简求值： $(\frac{x^{2}}{x^{2} - 1} - 1) \div \frac{1}{x^{2} + x}$ ，其中 $x = \frac{1}{2}$ ．

查看试题解析
15. 如图是由2个全等的正方形错位叠放组成的图形，请仅用没有刻度的直尺按要求完成下列作图．

(1)、在图1中画一个平行四边形（要求所画出的平行四边形不是矩形）；

(2)、在图2中画一个菱形（要求所画出的菱形不是正方形）．

查看试题解析
16. 《笠翁对韵》是明末清初著名戏曲家李渔的作品，是学习写作近体诗、词，用来熟悉对仗、用韵、组织词语的启蒙读物，“天对地，雨对风．大陆对长空．山花对海树，赤日对苍穹……”就是其中的句子．现将“A ．天”，“B ．地”，“C ．雨”，“D ．风”，“E ．大陆”，“F长空”分别书写在材质、大小完全相同的6张卡片上，洗匀后背面朝上．

(1)、第一次抽取时先抽取了一张，翻开后是“A ．天”，那么在剩下的五张卡片中恰好抽取得到卡片“B ．地”，使得对仗工整的概率是；

(2)、若第一次已经把“A ．天”、“B ．地”两张卡片抽走，第二次在剩下的四张卡片中随机抽取两张，请用列表或画树状图的方法求出能够对仗工整的概率．

查看试题解析
17. 某工厂现有甲种原料10吨，乙种原料15吨，计划用这两种原料生产A、B两种产品，两种原料都恰好全部用完．生产一件A、一件B产品与所需原料情况如下表所示：

甲种原料（吨）

乙种原料（吨）

A产品（件）

1

3

B产品（件）

2

1

(1)、求该厂生产A、B两种产品各有多少件；

(2)、如果购买这批原料共花费5万元，A、B产品的销售单价分别为2万元/件和3万元/件，求全部销售这批产品获得的利润是多少万元．

查看试题解析

18. 王老师对他所教的九（1），九（2）两个班级的学生进行了一次检测，批阅后对其中一道试题的得分情况进行了归类统计（各类别的得分如下表）．并绘制了如图所示的每班各类别得分人数的统计图（不完整）．

各类别的得分表

类别	得分
A：没有作答	0
B：解答但没有正确	1
C：仅做对第（1）问	3
D：完成正确	6

九（1）班各类别得分条形统计图

九（2）班各类别得分扇形统计图

已知两个班一共有50％的学生得6分．其中九（2）班得6分的学生有22人，九（2）班这道试题的平均得分为 $3.7$ 分．请解决如下问题：

(1)、九（2）班有名学生，两个班共有名学生；

(2)、补全条形统计图；

(3)、求m，n的值．

查看试题解析

19. 图1是一种可折叠台灯，它放置在水平桌面上，将其抽象成图2，其中点B，E，D均为可转动点．现测得 $A B = B E = E D = C D = 14 cm$ ，经多次调试发现当点B，E所在直线垂直径过 $C D$ 的中点F时（如图3所示）放置较平稳．

(1)、求平稳放置时灯座 $D C$ 与灯杆 $D E$ 的夹角的大小；

(2)、为保护视力，写字时眼睛离桌面的距离应保持在 $30 c m$ ，为防止台灯刺眼，点A离桌面的距离应不超过 $30 c m$ ，求台灯平稳放置时 $∠ A B E$ 的最大值．（结果精确到 $0.01 °$ ，参考数据： $\sqrt{3} \approx 1.732$ ， $sin 16.07 ° \approx 0.2768$ ， $cos 73.93 ° \approx 0.2768$ ， $tan 15.47 ° \approx 0.2768$ ）

查看试题解析
20. 如图， $△ A B C$ 内接于 $⊙ O$ ， $C P$ 是 $⊙ O$ 的切线，点P在直径 $A B$ 的延长线上．

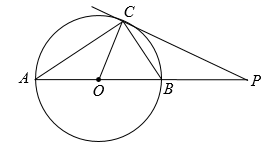(1)、特例探究：
若 $∠ A = 30 °$ ，则 $∠ P C B =$ °；

若 $∠ A = 50 °$ ，则 $∠ P C B =$ °；

(2)、数学结论：
猜想 $∠ P C B$ 与 $∠ A$ 的大小关系，请说明理由；

(3)、拓展应用：
若 $B C = \frac{2}{3} A C$ ， $A P = 4.5$ ，求 $P C$ 的长．

查看试题解析
21. 如图，在平面直角坐标系中，点B的坐标为 $(6 ， 4)$ ，反比例函数 $y = \frac{k}{x} (x > 0)$ 的图象交矩形 $O A B C$ 的边 $B C$ ， $A B$ 于D、E两点，连接 $D E$ ， $A C$ ．

(1)、当点D是 $B C$ 的中点时， $k =$ ，点E的坐标为；

(2)、设点D的横坐标为m．
①请用含m的代数式表示点E的坐标；

②求证： $D E // A C$ ．

查看试题解析
22. 已知抛物线 $C_{1} ： y = x^{2} - 4 x + 3 m$ 和 $C_{2} ： y = m x^{2} - 4 m x + 3 m$ ，其中 $m \neq 0$ 且 $m \neq 1$ ．

(1)、抛物线 $C_{1}$ 的对称轴是，抛物线 $C_{2}$ 的对称轴是；

(2)、这两条抛物线相交于点E，F（点E在点F的左侧），求E、F两点的坐标（用含m的代数式表示）并直接写出直线 $E F$ 与x轴的位置关系；

(3)、设抛物线 $C_{1}$ 的顶点为M， $C_{2}$ 的顶点为N；
①当m为何值时，点M与点N关于直线 $E F$ 对称？

②是否存在实数m，使得 $M N = 2 E F$ ？若存在，直接写出实数m的值，若不存在，请说明理由．

查看试题解析
23. 在 $Rt △ A B C$ 中， $∠ B A C = 90 °$ ， $A B = A C$ ，动点D在直线 $B C$ 上（不与点B，C重合），连接 $A D$ ，把 $A D$ 绕点A逆时针旋转90°得到 $A E$ ，连接 $D E$ ，F，G分别是 $D E$ ， $C D$ 的中点，连接 $F G$ ．

(1)、（特例感知）如图1，当点D是 $B C$ 的中点时， $F G$ 与 $B D$ 的数量关系是． $F G$ 与直线 $B C$ 的位置关系是．

(2)、（猜想论证）当点D在线段 $B C$ 上且不是 $B C$ 的中点时，（1）中的结论是否仍然成立？
①请在图2中补全图形；

②若成立，请给出证明；若不成立，请说明理由．

(3)、若 $A B = A C = \sqrt{2}$ ，其他条件不变，连接 $B F$ 、 $C F$ ．当 $△ A C F$ 是等边三角形时，（拓展应用）请直接写出 $△ B D F$ 的面积．

查看试题解析

	甲种原料（吨）	乙种原料（吨）
A产品（件）	1	3
B产品（件）	2	1