河北省石家庄新华区2021年中考数学模拟试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 下面四个图形中,∠1=∠2一定成立的是( )A、
 B、
B、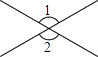 C、
C、 D、
D、 2. 如果a与b互为相反数,下列各式中错误的是( )A、 B、 C、 D、3. 如图,有 三个地点,且 ,从A地测得B地的方位角是北偏东 ,那么从C地测B地的方位角是( )
2. 如果a与b互为相反数,下列各式中错误的是( )A、 B、 C、 D、3. 如图,有 三个地点,且 ,从A地测得B地的方位角是北偏东 ,那么从C地测B地的方位角是( ) A、南偏东 B、南偏西 C、北偏东 D、北偏西4. 用四舍五入法对0.06045取近似值,错误的是( )A、0.1(精确到0.1) B、0.06(精确到百分位) C、0.061(精确到千分位) D、0.0605(精确到0.0001)5. 如图是由多个相同小立方体搭成的几何体的三视图,则这个几何体是( )
A、南偏东 B、南偏西 C、北偏东 D、北偏西4. 用四舍五入法对0.06045取近似值,错误的是( )A、0.1(精确到0.1) B、0.06(精确到百分位) C、0.061(精确到千分位) D、0.0605(精确到0.0001)5. 如图是由多个相同小立方体搭成的几何体的三视图,则这个几何体是( ) A、
A、 B、
B、 C、
C、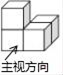 D、
D、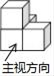 6. 长江比黄河长 ,黄河长度的6倍比长江长度的5倍多 ,设长江长度为 ,则下列方程中正确的是( )A、 B、 C、 D、7. 如图,在 中, .小丽按照下列方法作图:
6. 长江比黄河长 ,黄河长度的6倍比长江长度的5倍多 ,设长江长度为 ,则下列方程中正确的是( )A、 B、 C、 D、7. 如图,在 中, .小丽按照下列方法作图:①作 的角平分线 ,交 于点D;
②作 的垂直平分线,交 于点E .
根据小丽画出的图形,判断下列说法中正确的是( )
 A、点E是 的外心 B、点E是 的内心 C、点E在 的平分线上 D、点E到 边的距离相等8. 某市公园的东、西、南、北方向上各有一个入口,周末佳佳和琪琪随机从一个入口进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是( )A、 B、 C、 D、9. 如图,矩形 的中心位于直角坐标系的坐标原点O , 其面积为8,反比例函数 的图象经过点D , 则m的值为( )
A、点E是 的外心 B、点E是 的内心 C、点E在 的平分线上 D、点E到 边的距离相等8. 某市公园的东、西、南、北方向上各有一个入口,周末佳佳和琪琪随机从一个入口进入该公园游玩,则佳佳和琪琪恰好从同一个入口进入该公园的概率是( )A、 B、 C、 D、9. 如图,矩形 的中心位于直角坐标系的坐标原点O , 其面积为8,反比例函数 的图象经过点D , 则m的值为( ) A、2 B、4 C、6 D、810. 三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )
A、2 B、4 C、6 D、810. 三个全等三角形按如图的形式摆放,则∠1+∠2+∠3的度数是( )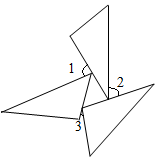 A、 B、 C、 D、11. 已知关于x的一元二次方程 没有实数解,则k的取值范围是( )A、 B、 且 C、 D、 且12. 如图, 为 的直径,C为半圆的中点,D为 上的一点,且 两点分别在 的异侧,则 的度数为( )
A、 B、 C、 D、11. 已知关于x的一元二次方程 没有实数解,则k的取值范围是( )A、 B、 且 C、 D、 且12. 如图, 为 的直径,C为半圆的中点,D为 上的一点,且 两点分别在 的异侧,则 的度数为( )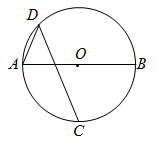 A、 B、 C、 D、13. 如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为( )
A、 B、 C、 D、13. 如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为( )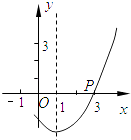 A、0 B、-1 C、1 D、214. 如图,在 中, ,用尺规作图,作 的平分线交 于点D , 则下列说法中:
A、0 B、-1 C、1 D、214. 如图,在 中, ,用尺规作图,作 的平分线交 于点D , 则下列说法中:①若连接 ,则 ;
② ;
③点D在 的中垂线上;
④ .
其中正确的个数是( )
 A、1 B、2 C、3 D、415. 把直线 向上平移m个单位后,与直线 的交点在第二象限,则m可以取得的整数值有( )A、4个 B、5个 C、6个 D、7个16. 如图, 是边长为4的等边 的中位线,动点P以每秒1个单位长度的速度,从点A出发,沿折线 向点E运动;同时动点Q以相同的速度,从点B出发,沿 向点C运动,当点P到达终点时,点Q同时停止运动.设运动时间为 四点围成图形的面积S与时间t之间的函数图象是( )
A、1 B、2 C、3 D、415. 把直线 向上平移m个单位后,与直线 的交点在第二象限,则m可以取得的整数值有( )A、4个 B、5个 C、6个 D、7个16. 如图, 是边长为4的等边 的中位线,动点P以每秒1个单位长度的速度,从点A出发,沿折线 向点E运动;同时动点Q以相同的速度,从点B出发,沿 向点C运动,当点P到达终点时,点Q同时停止运动.设运动时间为 四点围成图形的面积S与时间t之间的函数图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
17. 如果一个数的倒数是2021,则这个数为 .18. 是方程 的解,a的值为 .19. 如图,正方形 的边长为3,连接 两点分别在 的延长线上,且满足 .
 (1)、 的长为;(2)、当 平分 时, 的数量关系为;(3)、当 不平分 时, .
(1)、 的长为;(2)、当 平分 时, 的数量关系为;(3)、当 不平分 时, .三、解答题
-
20. 嘉琪通过计算和化简下列两式,发现了一个结论,请你帮助嘉琪完成这一过程.(1)、计算: ;(2)、化简: ;(3)、请写出嘉琪发现的结论.21. 某学校为了了解九年级学生的体育成绩,对九年级全体800名学生进行了男生1000米跑(女生800米跑),立定跳远、掷实心球三个项目的测试,每个项目满分10分,共30分.从中抽取了部分学生的成绩进行了统计(成绩均为整数),请根据尚未完成的频率分布表和频数分布直方图(如图),解答下列问题:
频率分布表
分数段
频数
频率
1
0.02
5
0.1
6
0.12
m
0.46
15
n
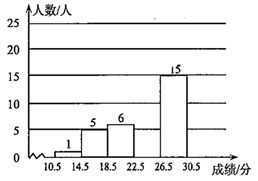 (1)、这次抽取了名学生的体育成绩进行统计,其中: , .(2)、补全频数分布直方图.(3)、学生成绩的中位数落在哪个分数段内?为什么?(4)、如果23分(包括23分)以上为良好,估测该学校体育成绩良好的学生大约有多少人?22. 已知:如图,在 中,E为 的中点,连接 并延长交 的延长线于点F , 连接 .
(1)、这次抽取了名学生的体育成绩进行统计,其中: , .(2)、补全频数分布直方图.(3)、学生成绩的中位数落在哪个分数段内?为什么?(4)、如果23分(包括23分)以上为良好,估测该学校体育成绩良好的学生大约有多少人?22. 已知:如图,在 中,E为 的中点,连接 并延长交 的延长线于点F , 连接 . (1)、求证: ;(2)、嘉琪说:“添加一个条件,能使四边形 是矩形”,你是否同意嘉琪的观点,如果同意,请添加一个条件,并给出证明;如果不同意,请说明理由.23. 如图,在平面直角坐标系中,直线 经过第一象限的点 和点 ,且 ,过点 作 轴,垂足为 , 的面积为 .
(1)、求证: ;(2)、嘉琪说:“添加一个条件,能使四边形 是矩形”,你是否同意嘉琪的观点,如果同意,请添加一个条件,并给出证明;如果不同意,请说明理由.23. 如图,在平面直角坐标系中,直线 经过第一象限的点 和点 ,且 ,过点 作 轴,垂足为 , 的面积为 . (1)、求B点的坐标;(2)、求直线 的函数表达式;(3)、直线 经过线段 上一点P(P不与A、B重合),求a的取值范围.24. 如图,在 中, ,以点O为圆心、2为半径画圆,过点A作 的切线,切点为P , 连接 .将 绕点O按逆时针方向旋转到 时,连接 .设旋转角为 .
(1)、求B点的坐标;(2)、求直线 的函数表达式;(3)、直线 经过线段 上一点P(P不与A、B重合),求a的取值范围.24. 如图,在 中, ,以点O为圆心、2为半径画圆,过点A作 的切线,切点为P , 连接 .将 绕点O按逆时针方向旋转到 时,连接 .设旋转角为 .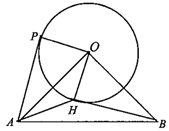 (1)、当 时,求证: 是 的切线;(2)、当 与 相切时,求旋转角 和点H运动路径的长;(3)、当 面积最大时,请直接写出此时点H到 的距离.25. 某商店试销一种成本为10元/件的工艺品,设售价为x(元/件),每天销量为y(件).经市场调查得知:y与 成正比例,且当 时, .(1)、求y与x之间的函数关系式;(2)、当x为何值时,商店试销该工艺品每天获得的利润最大?最大利润是多少?(3)、物价部门规定,该工艺品售价最高不能超过35元/件,那么售价定为多少时,商店试销该工艺品每天获得的利润最大?26. 如图,在 中, .动点P从点A出发,以每秒3个单位长度的速度沿 方向绕行 一周,动直线l从 开始,以每秒1个单位长度的速度向右平移,分别交 于 两点.当点P运动到点A时,直线l也停止运动.
(1)、当 时,求证: 是 的切线;(2)、当 与 相切时,求旋转角 和点H运动路径的长;(3)、当 面积最大时,请直接写出此时点H到 的距离.25. 某商店试销一种成本为10元/件的工艺品,设售价为x(元/件),每天销量为y(件).经市场调查得知:y与 成正比例,且当 时, .(1)、求y与x之间的函数关系式;(2)、当x为何值时,商店试销该工艺品每天获得的利润最大?最大利润是多少?(3)、物价部门规定,该工艺品售价最高不能超过35元/件,那么售价定为多少时,商店试销该工艺品每天获得的利润最大?26. 如图,在 中, .动点P从点A出发,以每秒3个单位长度的速度沿 方向绕行 一周,动直线l从 开始,以每秒1个单位长度的速度向右平移,分别交 于 两点.当点P运动到点A时,直线l也停止运动. (1)、求点P到 的最大距离;(2)、当点P在 上运动时,
(1)、求点P到 的最大距离;(2)、当点P在 上运动时,①求 的值;
②把 绕点E顺时针方向旋转,当点P的对应点 落在 上时, 的对应线段 恰好与 垂直,求此时t的值.
(3)、当点P关于直线 的对称点为F时,四边形 能否成为菱形?若能,直接写出t的值;若不能,请说明理由.