河北省石家庄市裕华区2021年中考数学3月模拟试卷
试卷更新日期：2021-05-14 类型：中考模拟
一、单选题
-
1. 如图，在一副三角板中，标识了4个角，其中最大的角为（ ）
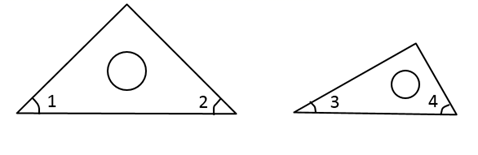A、∠1 B、∠2 C、∠3 D、∠42. 计算﹣1□1＝﹣2，则“□”表示的运算符号是（ ）A、+ B、﹣ C、× D、÷3. 如图，沿笔直小路DE的一侧栽植两棵小树B ， C ， 小明在A处测得AB＝5米，AC＝7米，则点A到DE的距离可能为（ ）
A、4米 B、5米 C、6米 D、7米4. 如图，是某几何体的三视图，则该几何体可能为（ ）
A、球 B、正方体 C、长方体 D、圆柱5. 下列各式从左到右的变形中，错误的是（ ）A、 B、 C、 D、6. 下面是解不等式 的过程，每一步只对上一步负责．则其中有错的步骤是（ ）
A、只有④ B、①③ C、②④ D、①②④7. 如图，将透明直尺叠放在正五边形之上，若正五边形有两个顶点在直尺的边上，且有一边与直尺的边垂直．则∠α＝（ ）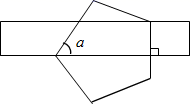
A、60° B、28° C、54° D、72°8. 嘉淇同学进行立定跳远练习，一共练习了7次，将成绩制成如图所示的折线统计图（成绩为整数，满分10分）．若嘉淇同学又跳了一次，成绩恰好是原来7次成绩的中位数，则这8次成绩和原来7次成绩相比（ ）
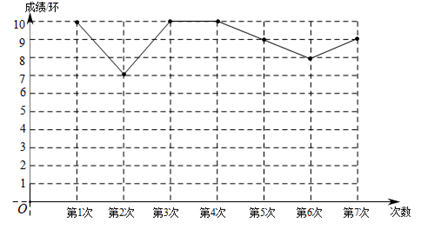A、众数没变，方差变小 B、众数没变，方差变大 C、中位数没变，方差变小 D、中位数没变，方差变大9. 若k为正整数，则（k2）3表示的是（ ）A、3个（k2）相加 B、2个（k3）相加 C、3个（k2）相乘 D、5个k相乘10. 如图，在6×4的小正方形网格中，小正方形的边长均为1，点A ， B ， C ， D ， E均在格点上．则∠ABC﹣∠DCE＝（ ）
A、30° B、42° C、45° D、50°11. 全国已有29个省份在政府工作报告中设定：2021年GDP增速目标不低于6%．已知河北省2020年GDP总量为36206.9亿元，若今年比上年增长6%，则河北省2021年GDP总量用科学记数法（精确到百亿位）表示为（ ）A、5.8×1011元 B、3.41×1012元 C、3.83×1012元 D、3.84×1012元12. 如图，在Rt△ABC中，∠C＝90°，tanB＝tanα＝ ，小明在图中用尺规完成了一些作图，根据作图痕迹，可以得到cos2α＝（ ）
A、 B、 C、 D、13. 若直线y＝ax（a≠0）和双曲线 （c≠0）在同一坐标系内的图象没有交点，且关于x的一元二次方程ax2+bx+c＝0的根的情况三人的说法如下：甲：方程可能有两个相等的实数根；
乙：方程没有实数根；
丙：x＝0一定不是方程的根．
下列判断正确的是（ ）
A、乙错丙对 B、乙对丙错 C、乙和丙都错 D、甲错乙对14. 如图，⊙O的半径为5，弦AB＝8，D是优弧AB上一点，则sinD＝（ ）
A、 B、 C、 D、15. 如图，锐角∠BOC＝α，∠AOC是它的邻补角，AD OC ， OD平分∠AOC ， P为射线OC上一点（不含端点O），连接PD ， 作∠DPE＝α，PE交直线AB于点E ． 甲、乙、丙、丁四位同学都对这个问题进行了研究，并得出自己的结论．甲：若点E与点O重合，四边形PEAD是菱形；
乙：若α＝60°，一定PD＝PE；
丙：若α≠60°，一定PD≠PE；
丁：若α＝80°，可能PD＝PE ．
下列判断正确的是（ ）
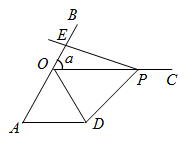A、甲、乙、丙正确，丁不正确 B、甲、乙、丁正确，丙不正确 C、甲、乙正确，丙、丁不正确 D、甲、乙、丁不正确，丙正确16. 如图1，一个移动喷灌架喷射出的水流可以近似地看成抛物线．图2是喷灌架为一坡地草坪喷水的平面示意图，喷水头的高度（喷水头距喷灌架底部的距离）是1米．当喷射出的水流距离喷水头20米时．达到最大高度11米，现将喷灌架置于坡度为1：10的坡地底部点O处，草坡上距离O的水平距离为30米处有一棵高度约为2.3米的石榴树AB ， 因为刚刚被喷洒了农药，近期不能被喷灌．下列说法正确的是（ ）
A、水流运行轨迹满足函数y＝﹣ x2﹣x+1 B、水流喷射的最远水平距离是40米 C、喷射出的水流与坡面OA之间的最大铅直高度是9.1米 D、若将喷灌架向后移动7米，可以避开对这棵石榴树的喷灌二、填空题
-
17. 的立方根是 ．18. 如图，在四边形ABCD中，∠B＝90°，AB＝3，BC＝6，点E在BC上，AE⊥DE ． 且AE＝DE ， 若EC＝1．则CD＝ ．
19. 如图，在平面直角坐标系xOy中，等边三角形△AOB的顶点A在第一象限，点B（3，0），双曲线 （k＞0，x＞0）把△AOB分成两部分．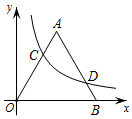
(1)、双曲线与边OA ， AB分别交于C ， D两点，若OC＝2，则k＝ ， 点D的横坐标为；(2)、横纵坐标都为整数的点称为整点，若双曲线 （k＞0，x＞0）把△AOB分成的两部分内的整点个数相等（不含边界），则k的取值范围为 ．三、解答题
-
20. 已知有理数﹣9，7，14在数轴上对应的点分别为A ， B ， C ．(1)、若数轴上点D对应的数为 ，求线段AD的长；(2)、再添加一个数a ， 数轴上点E对应的数为﹣9，7，14和a四个数的平均数，若线段DE＝1，求a的值．21. 如图，A ， B两张卡片除内容外完全相同，现将两张卡片扣在桌面上，随机抽取一张，将抽中卡片上的整式各项改变符号后与未抽中卡片上的整式相加，并将结果化简得到整式C ．
(1)、若抽中的卡片是B ．①求整式C；
②当x＝ ﹣1时，求整式C的值．
(2)、若无论x取何值，整式C的值都是非负数，请通过计算，判断抽到的是哪张卡片？22. 临近元宵节，嘉琪家从网上购买了4箱“库尔勒”香梨，但开箱验货后，发现其中混入了若干“红酥梨”．统计后发现每箱中最多混入了2个“红酥梨”，具体数据见表：每箱混入“红酥梨”个数/个
0
1
2
箱数/箱
1
m
n
(1)、若从4箱中任意选取1箱，则事件“箱中没有混入‘红酥梨’”是 ．A ． 必然事件 B ． 随机事件 C ． 不可能事件 D ． 确定事件
(2)、若事件“每箱中混入1个‘红酥梨’”的概率为 ．①求m和n的值；
②嘉琪准备将其中两箱送给舅舅，他从4箱中随机挑选了两箱，用列表法求两箱中一共混入了1个“红酥梨”的概率．
23. 如图，在△ABC中，AB＝AC＝2 ，∠BAC＝120°，点D在AB上，AD＝2，以点A为圆心，AD长为半径的弧交AC于点E ， 与BC交于点F ， G ， P是 上一点．将AP绕点A逆时针旋转120°，得到AQ ， 连接CQ ， AF ．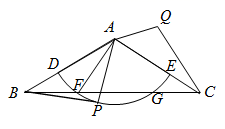
(1)、若BP与 所在圆相切，判断CQ与 所在圆的位置关系．并加以证明；(2)、求BF的长及扇形EAF的面积；(3)、若∠PAB＝m°，当∠ACQ＝30°，直接写出m的值．24. 某旅游团乘坐旅游中巴车以50千米/时的速度匀速从甲地到相距200千米的乙地旅游．行驶了80千米时，车辆出现故障，与此同时，得知这个情况的乙地旅行社立刻派出客车以80千米/时的速度前来接应．相遇后，旅游团用了18分钟从旅游中巴换乘到客车上，随后以v（千米/时）的速度匀速到达乙地．设旅游团离开甲地的时间为x（小时），旅游中巴车距离乙地的路程为y1（千米），客车在遇到旅游团前离开乙地的路程y2（千米）．(1)、若v＝80千米/时，①y1与x的函数表达式为 ．
②求y2与x的函数表达式，并写出x的取值范围．
(2)、设旅游团从甲地到乙地所用的总时间为T（小时），求T（小时）与v（千米/时）的函数关系式（不写v的取值范围）．(3)、旅游团要求到达时间比按原来的旅游中巴正常到达乙地的时间最多晚1个小时，问客车返回乙地的车速至少为每小时多少千米？25. 如图，抛物线L：y＝ax2+bx﹣3与r轴交于A（﹣2，0），B（6，0）．与y轴交于点C ， 点P的坐标为（m ， ﹣ m﹣1）．
(1)、请求出L的解析式及对称轴．(2)、当点P在L上时，求m的值．(3)、过点P作x轴的垂线，分别与x轴、抛物线L交于点M ， N ．①当线段PN＝ 时，求m的值；
②若点P ， M ， N三点不重合，当其中两点关于第三点对称时，直接写出m的值．
26. 如图，在矩形ABCD中，AB＝8，BC＝12，点E在AB上，AE＝5，P是AD上一点，将矩形沿PE折叠，点A落在点 处．连接AC ， 与PE相交于点F ， 设AP＝x ．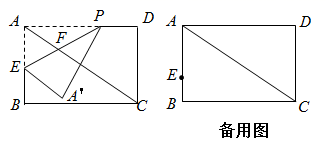
(1)、AC＝；(2)、若点 在∠BAC的平分线上，求FC的长；(3)、求点 ，D距离的最小值，并求此时tan∠APE的值；(4)、若点 在△ABC的内部，直接写出x的取值范围．