河北省石家庄市十八县重点中学2021年中考数学模拟试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列事件中,属于不可能事件的是( )A、射击运动员射击一次,命中9环 B、某种彩票中奖率为10%,买10张有1张中奖 C、今天是星期六,明天就是星期一 D、在只装有10个红球的布袋中摸出1个球,这个球一定是红球3. 由4个完全相同的小正方体组成的立体图形如图所示,则该立体图形的俯视图是( )
2. 下列事件中,属于不可能事件的是( )A、射击运动员射击一次,命中9环 B、某种彩票中奖率为10%,买10张有1张中奖 C、今天是星期六,明天就是星期一 D、在只装有10个红球的布袋中摸出1个球,这个球一定是红球3. 由4个完全相同的小正方体组成的立体图形如图所示,则该立体图形的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 将一元二次方程 化成 (a,b为常数)的形式,则a,b的值分别是( )A、 ,21 B、 ,11 C、4,21 D、 ,695. 反比例函数 的图象经过点 ,则下列说法错误的是( )A、 B、函数图象分布在第一、三象限 C、y随x的增大而减小 D、当 时,y随x的增大而减小6. 如图,是小明绘制的他在一周内每天跑步圈数的折线统计图.下列结论正确的是( )
4. 将一元二次方程 化成 (a,b为常数)的形式,则a,b的值分别是( )A、 ,21 B、 ,11 C、4,21 D、 ,695. 反比例函数 的图象经过点 ,则下列说法错误的是( )A、 B、函数图象分布在第一、三象限 C、y随x的增大而减小 D、当 时,y随x的增大而减小6. 如图,是小明绘制的他在一周内每天跑步圈数的折线统计图.下列结论正确的是( )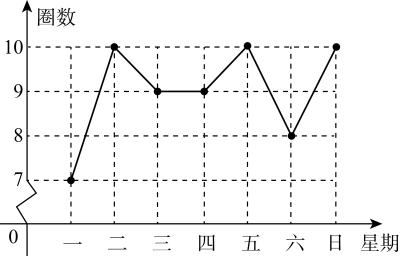 A、众数是9 B、中位数是8.5 C、平均数是9 D、方差是77. 如图, 是 的直径, , 是 的弦,连接 ,若 ,则 的度数是( )
A、众数是9 B、中位数是8.5 C、平均数是9 D、方差是77. 如图, 是 的直径, , 是 的弦,连接 ,若 ,则 的度数是( )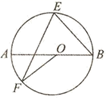 A、 B、 C、 D、8. 根据圆规作图的痕迹,可用直尺成功地找到三角形内心的是( )A、
A、 B、 C、 D、8. 根据圆规作图的痕迹,可用直尺成功地找到三角形内心的是( )A、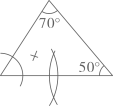 B、
B、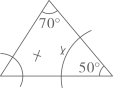 C、
C、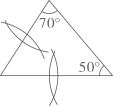 D、
D、 9. 某射击运动员在同一条件下的射击成绩记录如下:
9. 某射击运动员在同一条件下的射击成绩记录如下:射击次数
20
80
100
200
400
1000
“射中九环以上”的次数
18
68
82
168
327
823
“射中九环以上”的频率(结果保留两位小数)
0.90
0.85
0.82
0.84
0.82
0.82
根据频率的稳定性,估计这名运动员射击一次时“射中九环以上”的概率约是( )
A、0.90 B、0.82 C、0.85 D、0.8410. 国家统计局统计数据 显示,我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为( )A、 B、 C、 D、11. 在平面直角坐标系中, 和 的相似比等于 ,并且是关于原点O的位似图形,若点A的坐标为 ,则其对应点A的坐标是( )A、 B、 C、 或 D、 或12. 如图,现要在抛物线 上找点 ;针对b的不同取值,所找点P的个数,三人的说法如下,
甲:若 ,则点P的个数为0;
乙:若 ,则点P的个数为1;
丙:若 ,则点P的个数为1.
下列判断正确的是( )
A、乙错,丙对 B、甲和乙都错 C、乙对,丙错 D、甲错,丙对13. 如图, 中, .将 绕点B逆时针旋转得到 ,使点C的对应点 恰好落在边 上,则 的度数是( ) A、 B、 C、 D、14. 定义新运算 ,对于任意实数a,b满足 ,其中等式右边是通常的加法、减法、乘法运算,例如 ,若 (k为实数) 是关于x的方程,则它的根的情况是( )A、有一个实根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根15. 如图,A,B两地相距am,它们之间有一半径为r的圆形绿地(r< ),绿地圆心位于AB连线的中点O处,分别过A、B作⊙O的切线相交于C,切点分别为D、E.现规划两条驾车路径:①B→E→C→D→A;②B→E→(沿 )→D→A,则下列说法正确的是( )
A、 B、 C、 D、14. 定义新运算 ,对于任意实数a,b满足 ,其中等式右边是通常的加法、减法、乘法运算,例如 ,若 (k为实数) 是关于x的方程,则它的根的情况是( )A、有一个实根 B、有两个不相等的实数根 C、有两个相等的实数根 D、没有实数根15. 如图,A,B两地相距am,它们之间有一半径为r的圆形绿地(r< ),绿地圆心位于AB连线的中点O处,分别过A、B作⊙O的切线相交于C,切点分别为D、E.现规划两条驾车路径:①B→E→C→D→A;②B→E→(沿 )→D→A,则下列说法正确的是( )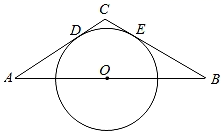 A、①较长 B、②较长 C、①②一样长 D、以上皆有可能16. 如图,抛物线 与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 ,则下列结论中:① ;② ;③ 与 是抛物线上两点,若 ,则 ;④若抛物线的对称轴是直线 ,m为任意实数,则 ;⑤若 ,则 ,正确的个数是( )
A、①较长 B、②较长 C、①②一样长 D、以上皆有可能16. 如图,抛物线 与x轴正半轴交于A,B两点,与y轴负半轴交于点C.若点 ,则下列结论中:① ;② ;③ 与 是抛物线上两点,若 ,则 ;④若抛物线的对称轴是直线 ,m为任意实数,则 ;⑤若 ,则 ,正确的个数是( )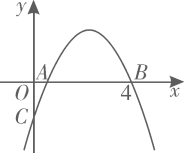 A、5 B、4 C、3 D、2
A、5 B、4 C、3 D、2二、解答题
-
17. 计算:18. 小明在解方程x2﹣5x=1时出现了不符合题意,解答过程如下:
∵a=1,b=﹣5,c=1,(第一步)
∴b2﹣4ac=(﹣5)2﹣4×1×1=21(第二步)
∴ (第三步)
∴ , (第四步)
(1)、小明解答过程是从第步开始出错的,其错误原因是 .(2)、写出此题正确的解答过程.19. 如图,在平面直角坐标系中, 的顶点坐标为 、 、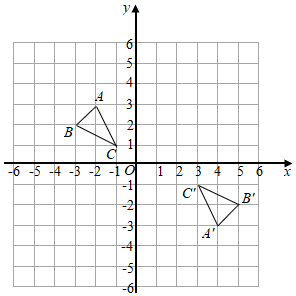 (1)、画出 绕原点顺时针旋转 后得到的 ,并求出 扫过的面积;(2)、若 与 是中心对称图形,则对称中心的坐标为 .20. 今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.
(1)、画出 绕原点顺时针旋转 后得到的 ,并求出 扫过的面积;(2)、若 与 是中心对称图形,则对称中心的坐标为 .20. 今年某市为创评“全国文明城市”称号,周末团市委组织志愿者进行宣传活动.班主任梁老师决定从4名女班干部(小悦、小惠、小艳和小倩)中通过抽签的方式确定2名女生去参加.抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
(1)、该班男生“小刚被抽中”是事件,“小悦被抽中”是事件(填“不可能”或“必然”或“随机”);第一次抽取卡片“小悦被抽中”的概率为;(2)、试用画树状图或列表的方法表示这次抽签所有可能的结果,并求出“小惠被抽中”的概率.21. 如图,小明利用学到的数学知识测量大桥主架在水面以上的高度 ,在观测点C处测得大桥主架顶端A的仰角为30°,测得大桥主架与水面交汇点B的俯角为14°,观测点与大桥主架的水平距离 为60米,且 垂直于桥面.(点 在同一平面内) (1)、求大桥主架在桥面以上的高度 ;(结果保留根号)(2)、求大桥主架在水面以上的高度 .(结果精确到1米)
(1)、求大桥主架在桥面以上的高度 ;(结果保留根号)(2)、求大桥主架在水面以上的高度 .(结果精确到1米)(参考数据 )
22. 如图,一次函数 的图象与反比例函数 ( 为常数且 )的图象相交于 ,B两点.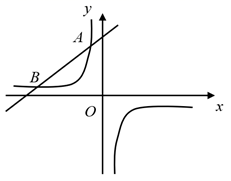 (1)、求反比例函数的表达式;(2)、将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求b的值.23. 某公司购进一批受环境影响较大的商品,需要在特定的环境中才能保存,已知该商品成本y(元/件)与保存的时间第x(天)之间的关系满足y=x2﹣4x+100,该商品售价p(元/件)与保存时间第x(天)之间满足一次函数关系,其对应数据如表:
(1)、求反比例函数的表达式;(2)、将一次函数 的图象沿 轴向下平移 个单位 ,使平移后的图象与反比例函数 的图象有且只有一个交点,求b的值.23. 某公司购进一批受环境影响较大的商品,需要在特定的环境中才能保存,已知该商品成本y(元/件)与保存的时间第x(天)之间的关系满足y=x2﹣4x+100,该商品售价p(元/件)与保存时间第x(天)之间满足一次函数关系,其对应数据如表:x(天)
……
5
7
……
p(元/件)
……
248
264
……
(1)、求商品的售价p(元/件)与保存时间第x(天)之间的函数关系式;(2)、求保存第几天时,该商品不赚也不亏;(3)、请你帮助该公司确定在哪一天卖出,每件商品能获得最大利润,此时每件商品的售价是多少?24. 如图,在矩形 中, , ,O是 的中点,以O为圆心,在 的下方作半径为3的半圆O,交 于点E,F.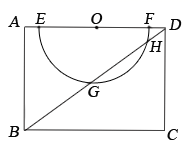
 (1)、思考:连接 ,交半圆O于点G、H,求 的长;(2)、探究:将线段 连带半圆O绕点A顺时针旋转,得到半圆 ,设其直径为 ,旋转角为 ( );
(1)、思考:连接 ,交半圆O于点G、H,求 的长;(2)、探究:将线段 连带半圆O绕点A顺时针旋转,得到半圆 ,设其直径为 ,旋转角为 ( );①设 到直线 的距离为m,当 时,求 的取值范围.
②若半圆 与线段 相切,或半圆 与线段 相切,设切点为R,直接写出 的长.( , , ,结果保留 )
三、填空题
-
25. “闻起来臭,吃起来香”的臭豆腐是长沙特色小吃,臭豆腐级小,但制作流程却比较复杂,其中在进行加工煎炸臭豆腐时,我们把“焦脆而不糊”的豆腐块数的百分比称为“可食用率”。在特定条件下,“可食用率” 与加工煎炸时间 (单位:min)近似满足的函数关系为: ( ; , , 是常数),如图记录了三次实验的数据.根据上述函数关系和实验数据,可以得到 与 的解析式为;并得到加工煎炸臭豆腐的最佳时间为 .
 26. 如图,在平面直角坐标系 中,半径为2的 与x轴的正半轴交于点A,点B是 上一动点,点C为弦 的中点,直线 与x轴、y轴分别交于点D、E,则 面积的最小值为; 面积的最大值为 .
26. 如图,在平面直角坐标系 中,半径为2的 与x轴的正半轴交于点A,点B是 上一动点,点C为弦 的中点,直线 与x轴、y轴分别交于点D、E,则 面积的最小值为; 面积的最大值为 .