北京市门头沟区2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 如图,在 中,BC边上的高是( )
 A、CD B、AE C、AF D、AH2. 根据国家卫健委官网统计,截至2021年4月10日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗16447.1万剂次,将16447.1万用科学记数法表示为( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、等边三角形
A、CD B、AE C、AF D、AH2. 根据国家卫健委官网统计,截至2021年4月10日,31个省(自治区、直辖市)和新疆生产建设兵团累计报告接种新冠病毒疫苗16447.1万剂次,将16447.1万用科学记数法表示为( )A、 B、 C、 D、3. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、等边三角形 B、平行四边形
B、平行四边形  C、等腰梯形圆
C、等腰梯形圆  D、圆
D、圆  4. 某个几何体的展开图如图所示,该几何体是( )
4. 某个几何体的展开图如图所示,该几何体是( )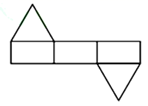 A、三棱柱 B、三棱锥 C、长方体 D、圆柱5. 内角和与外角和相等的多边形是( )A、六边形 B、五边形 C、四边形 D、三角形6. 如图,直线AB , CD交于点O , 射线OE平分 ,若 ,则 等于( )
A、三棱柱 B、三棱锥 C、长方体 D、圆柱5. 内角和与外角和相等的多边形是( )A、六边形 B、五边形 C、四边形 D、三角形6. 如图,直线AB , CD交于点O , 射线OE平分 ,若 ,则 等于( )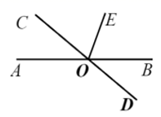 A、 B、 C、 D、7. 点a , b在数轴上的位置如图所示,且满足 , ,则原点所在的位置有可能是( )
A、 B、 C、 D、7. 点a , b在数轴上的位置如图所示,且满足 , ,则原点所在的位置有可能是( )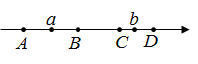 A、点A B、点B C、点C D、点D8. 在物理实验室实验中,为了研究杠杆的平衡条件,设计了如下实验,如图,铁架台左侧钩码的个数与位置都不变,在保证杠杆水平平衡的条件下,右侧采取变动钩码数量即改变力F , 或调整钩码位置即改变力臂L , 确保杠杆水平平衡,则力F与力臂L满足的函数关系是( )
A、点A B、点B C、点C D、点D8. 在物理实验室实验中,为了研究杠杆的平衡条件,设计了如下实验,如图,铁架台左侧钩码的个数与位置都不变,在保证杠杆水平平衡的条件下,右侧采取变动钩码数量即改变力F , 或调整钩码位置即改变力臂L , 确保杠杆水平平衡,则力F与力臂L满足的函数关系是( ) A、正比例函数关系 B、反比例函数关系 C、一次函数关系 D、二次函数关系
A、正比例函数关系 B、反比例函数关系 C、一次函数关系 D、二次函数关系二、填空题
-
9. 若 在实数范围内有意义,则实数x的取值范围是.10. 如图所示的网格是正方形网格,点A , B , C是网格线交点,那么 .
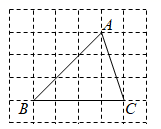 11. 请你写出一个大于2小于3的无理数是 .12. 已知 且 ,写出一组符合条件的值 .13. 关于 的一元二次方程 有两个实数根,则k的取值范围是 .14. 如图,在 中, , ,半径 ,则 .
11. 请你写出一个大于2小于3的无理数是 .12. 已知 且 ,写出一组符合条件的值 .13. 关于 的一元二次方程 有两个实数根,则k的取值范围是 .14. 如图,在 中, , ,半径 ,则 .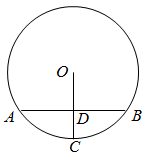 15. 下面是某小区随机抽取的100户家庭的月用电量情况统计表:
15. 下面是某小区随机抽取的100户家庭的月用电量情况统计表:月户用电量x(千瓦时/户.月)
户数(户)
5
22
27
31
15
从中任意抽出一个家庭进行用电情况调查,则抽到的家庭月用电量为第二档(用电量大于240小于等于400为第二档)的概率为 .
16. 以下是小亮的妈妈做晚饭的食材准备及加工时间列表,有一个炒菜锅,一个电饭煲,一个煲汤锅,两个燃气灶可用,做好这顿晚餐一般情况下至少需要分钟.用时
种类
准备时间(分钟)
加工时间(分钟)
米饭
3
30
炒菜1
5
6
炒菜2
5
8
汤
5
15
三、解答题
-
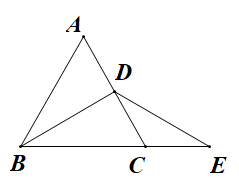
17. 计算: .18. 解不等式组:19. 已知,如图, 是等边三角形, 于D , E是BC延长线上的一点, .求 的度数.
 20. 已知 ,求代数式 的值.21. 已知: ,CD平分 .
20. 已知 ,求代数式 的值.21. 已知: ,CD平分 .求作:菱形DFCE , 使点F在BC边上,点E在AC边上,下面是尺规作图过程.
作法:①分别以C、D为圆心,大于 为半径作弧,两弧分别交于点M、N;
②作直线MN分别与AC、BC交于点E、F;
③连接DE、DF , DC与EF的交点记为点G;四边形DFCE为所求作的菱形.
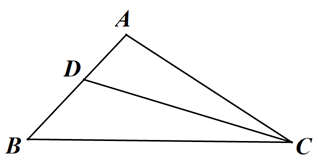 (1)、利用直尺和圆规依做法补全图形(保留作图痕迹);(2)、完成下面的证明.
(1)、利用直尺和圆规依做法补全图形(保留作图痕迹);(2)、完成下面的证明.证明: ,
为DC的垂直平分线.
,
.
平分 ,
.
,
▲ ▲ ( )(填推理依据)
同理可证 ,
四边形DFCE为平行四边形.
又 ▲ ,
四边形DFCE为菱形.
22. 已知:如图,在菱形ABCD中, 于点E , 延长AD至F , 使 ,连接CF .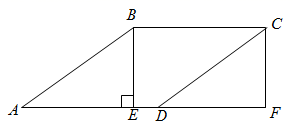 (1)、求证:四边形EBCF是矩形;(2)、若 , ,求AF的长.23. 在平面直角坐标系 中,正比例函数 与反比例函数 的图象相交于点
(1)、求证:四边形EBCF是矩形;(2)、若 , ,求AF的长.23. 在平面直角坐标系 中,正比例函数 与反比例函数 的图象相交于点 (1)、求k的值;(2)、过点 平行于x轴的直线,分别与第一象限内的正比例函数 、反比例函数 的图象相交于 ,当 时,求 的取值范围.24. 如图,AB是 的直径,C是 上一点,D是OB中点,过点D作AB的垂线交AC的延长线于点F , FD上有一点E , .
(1)、求k的值;(2)、过点 平行于x轴的直线,分别与第一象限内的正比例函数 、反比例函数 的图象相交于 ,当 时,求 的取值范围.24. 如图,AB是 的直径,C是 上一点,D是OB中点,过点D作AB的垂线交AC的延长线于点F , FD上有一点E , .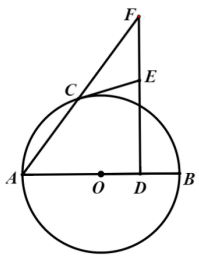 (1)、求证:CE是 的切线;(2)、如果 , ,求AB的长.25. 2021年是中国共产党成立100周年,某中学面向学校全体师生征集“礼赞百年”活动作品,作品类别包括征文、书法、绘画.该中学学生小明统计了学校30个教学班上交活动作品的数量(单位:份),相关信息如下:
(1)、求证:CE是 的切线;(2)、如果 , ,求AB的长.25. 2021年是中国共产党成立100周年,某中学面向学校全体师生征集“礼赞百年”活动作品,作品类别包括征文、书法、绘画.该中学学生小明统计了学校30个教学班上交活动作品的数量(单位:份),相关信息如下:a . 小明所在中学30个教学班上交作品的数量统计图:
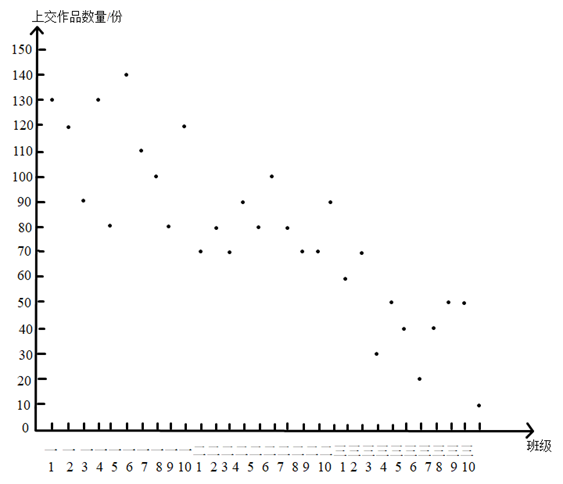 b . 小明所在中学各班学生上交作品数量的平均数如下:
b . 小明所在中学各班学生上交作品数量的平均数如下:班级
初一年级(10个班)
初二年级(10个班)
初三年级(10个班)
平均数
110
80
40
(1)、该中学各班学生上交作品数量的平均数约为(结果取整数);(2)、已知该中学全体教师上交作品的数量恰好是该校各班级中,上交作品数量最多的班级与最少的班级的数量差,则全体教师上交作品的数量为份;(3)、记该中学初一年级学生上交作品数量的方差为 ,初二年级学生上交作品数量的方差为 ,初三年级学生上交作品数量的方差为 .直接写出 , , 的大小关系.26. 在平面直角坐标系 中,已知关于x的二次函数 (1)、求该二次函数的对称轴;(2)、若点 在抛物线 上,试比较m、n的大小;(3)、 是抛物线 上的任意两点,若对于 且 ,都有 ,求t的取值范围.27. 在正方形ABCD中,将边AD绕点A逆时针旋转 得到线段AE , AE与CD延长线相交于点F , 过B作 交CF于点G , 连接BE.
(1)、求该二次函数的对称轴;(2)、若点 在抛物线 上,试比较m、n的大小;(3)、 是抛物线 上的任意两点,若对于 且 ,都有 ,求t的取值范围.27. 在正方形ABCD中,将边AD绕点A逆时针旋转 得到线段AE , AE与CD延长线相交于点F , 过B作 交CF于点G , 连接BE.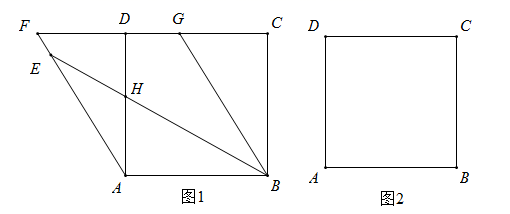 (1)、如图1,求证: ;(2)、当( )时,依题意补全图2,用等式表示线段 之间的数量关系,并证明.28. 在平面直角坐标系 中, 的半径为1,点A是平面内一点,过点A的直线交 于点 B和点C( ), ,我们把点 B称为点A关于 的“斜射点”.
(1)、如图1,求证: ;(2)、当( )时,依题意补全图2,用等式表示线段 之间的数量关系,并证明.28. 在平面直角坐标系 中, 的半径为1,点A是平面内一点,过点A的直线交 于点 B和点C( ), ,我们把点 B称为点A关于 的“斜射点”.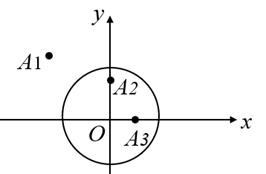 (1)、如图,在点 中,存在关于 的“斜射点”的是 .(2)、已知若 ,点关于 的“斜射点”为点B , 则点 B的坐标可以是 . (写出两个即可)(3)、若点A直线 上,点A关于 的“斜射点”为 ,画出示意图,直接写出 k的取值范围.
(1)、如图,在点 中,存在关于 的“斜射点”的是 .(2)、已知若 ,点关于 的“斜射点”为点B , 则点 B的坐标可以是 . (写出两个即可)(3)、若点A直线 上,点A关于 的“斜射点”为 ,画出示意图,直接写出 k的取值范围.