北京市海淀区2021年中考数学一模试卷
试卷更新日期:2021-05-14 类型:中考模拟
一、单选题
-
1. 如图是某几何体的视图,该几何体是( )
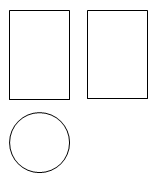 A、圆柱 B、球 C、三棱柱 D、长方体2. 2021年2月24日6时29分,我国自主研制的首个火星探测器“天问一号”成功实施第三次近火制动,进入近火点280千米、远火点59000千米、周期2个火星日的火星停泊轨道.将59000用科学记数法表示应为( )A、 B、 C、 D、3. 七巧板是我国的一种传统智力玩具.下列用七巧板拼成的图形中,是轴对称图形的是( )A、
A、圆柱 B、球 C、三棱柱 D、长方体2. 2021年2月24日6时29分,我国自主研制的首个火星探测器“天问一号”成功实施第三次近火制动,进入近火点280千米、远火点59000千米、周期2个火星日的火星停泊轨道.将59000用科学记数法表示应为( )A、 B、 C、 D、3. 七巧板是我国的一种传统智力玩具.下列用七巧板拼成的图形中,是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 如图是一个可以自由转动的转盘,转盘分成4个大小相同的扇形,颜色分为灰、白二种颜色.指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向白色区域的概率是( )
4. 如图是一个可以自由转动的转盘,转盘分成4个大小相同的扇形,颜色分为灰、白二种颜色.指针的位置固定,转动的转盘停止后,其中的某个扇形会恰好停在指针所指的位置(指针指向两个扇形的交线时,当作指向右边的扇形),则指针指向白色区域的概率是( )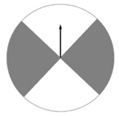 A、 B、 C、 D、15. 如果一个多边形的每一个外角都是60°,则这个多边形的边数是( )
A、 B、 C、 D、15. 如果一个多边形的每一个外角都是60°,则这个多边形的边数是( )
A、3 B、4 C、5 D、66. 实数a与b在数轴上对应点的位置如图所示.则正确的结论是( ) A、 B、 C、 D、7. 已知 是不等式 的解,b的值可以是( )A、4 B、2 C、0 D、8. 如图, 是 直径,点C、D将 分成相等的三段弧,点P在 上.已知点Q在 上且 ,则点Q所在的弧是( )
A、 B、 C、 D、7. 已知 是不等式 的解,b的值可以是( )A、4 B、2 C、0 D、8. 如图, 是 直径,点C、D将 分成相等的三段弧,点P在 上.已知点Q在 上且 ,则点Q所在的弧是( )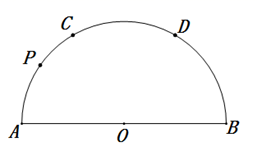 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 若代数式 有意义,则实数x 的取值范围是.10. 方程组 的解为.11. 如图,在一束平行光线中插入一张对边平行的纸板.如果图中 是 ,那么 的度数是 .
 12. 若 的值为有理数,请你写出一个符合条件的实数a的值 .13. 计算: .14. 已知关于x的方程 有两个相等的实数根,则m的值是 .15. 图1中的直角三角形有一条直角边长为3,将四个图1中的直角三角形分别拼成如图2,图3所示的正方形,其中阴影部分的面积分别记为 ,则 的值为 .
12. 若 的值为有理数,请你写出一个符合条件的实数a的值 .13. 计算: .14. 已知关于x的方程 有两个相等的实数根,则m的值是 .15. 图1中的直角三角形有一条直角边长为3,将四个图1中的直角三角形分别拼成如图2,图3所示的正方形,其中阴影部分的面积分别记为 ,则 的值为 . 16. 图1是一个 正方形网格,两条网格线的交点叫做格点.甲、乙两人在网格中进行游戏,规则如下:
16. 图1是一个 正方形网格,两条网格线的交点叫做格点.甲、乙两人在网格中进行游戏,规则如下:
游戏规则
a . 两人依次在网格中画线段,线段的起点和终点均为格点;
b . 新画线段的起点为前一条线段的终点,且与任意已画出线段不能有其他公共点;
c . 已画出线段的所有端点中,任意三个端点不能在同一条直线上;
d . 当某人无法画出新的线段时,则另一人获胜.
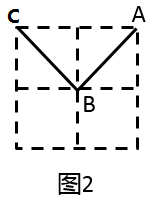
如图2,甲先画出线段 ,乙随后画出线段 .若这局游戏继续进行下去,最终的获胜者是 . (填“甲”,“乙”或“不确定”).
 17. 牛年伊始,中国电影行业迎来了开门红.春节档期全国总观影人次超过1.6亿,总票房超过80亿元.以下是甲、乙两部春节档影片上映后的票房信息.
17. 牛年伊始,中国电影行业迎来了开门红.春节档期全国总观影人次超过1.6亿,总票房超过80亿元.以下是甲、乙两部春节档影片上映后的票房信息.a . 两部影片上映第一周单日票房统计图.

b . 两部影片分时段累计票房如下
上映影片
2月12日-18日累计票房(亿元)
2月19-21日累计票房(亿元)
甲
31.56
乙
37.22
2.95
(以上数据来源于中国电影数据信息网)
根据以上信息,回答下列问题:
(1)、2月12日-18日的一周时间内,影片乙单日票房的中位数为;(2)、对于甲、乙两部影片上映第一周的单日票房,下列说法中所有正确结论的序号是;①甲的单日票房逐日增加;
②甲单日票房的方差小于乙单日票房的方差;
③在第一周的单日票房统计中,甲超过乙的差值于2月17日达到最大.
(3)、截止到2月21日,影片甲上映后的总票房超过了影片乙,据此估计,2月19日-21日三天内影片甲的累计票房应超过亿元.三、解答题
-
18. 计算: .19. 解不等式组:20. 如图,点B , E , C , F在一条直线上, .求证: .
 21. 已知 ,求代数式 的值.22. 如图,四边形 是矩形,点E是边 上一点, .
21. 已知 ,求代数式 的值.22. 如图,四边形 是矩形,点E是边 上一点, . (1)、求证: ;(2)、F为 延长线上一点,满足 ,连接 交 于点G . 若 ,求 的长.23. 我国是世界上最旱发明历法的国家之一.《周礼》中记载:垒土为主,立木为表,测日影,正地中,意四时.如图1,圭是地面上一根水平标尺,指向正北,表是一根垂直于地面的杆,正午,表的日影(即表影)落在圭上,根据表影的长度可以测定节气.
(1)、求证: ;(2)、F为 延长线上一点,满足 ,连接 交 于点G . 若 ,求 的长.23. 我国是世界上最旱发明历法的国家之一.《周礼》中记载:垒土为主,立木为表,测日影,正地中,意四时.如图1,圭是地面上一根水平标尺,指向正北,表是一根垂直于地面的杆,正午,表的日影(即表影)落在圭上,根据表影的长度可以测定节气.

在一次数学活动课上,要制作一个圭表模型.如图2,地面上放置一根长 的杆 ,向正北方向画一条射线 ,在 上取点D , 测得 .
(1)、判断:这个模型中 与 是否垂直.答:(填“是”或“否”);你的理由是: .(2)、某地部分节气正午时分太阳光线与地面夹角 的值,如下表:节气
夏至
秋分
冬至
太阳光线与地面夹角
①记夏至和冬至时表影分别为 和 ,利用上表数据,在射线 上标出点M和点N的位置;
②记秋分时的表影为 ,推测点P位于( )
A . 线段 中点左侧 B . 线段 中点处 C . 线段 中点右侧
24. 已知直线 过点 .点P为直线l上一点,其横坐标为m . 过点P作y轴的垂线,与函数 的图象交于点Q .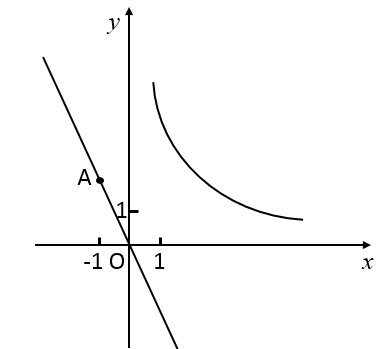 (1)、求k的值;(2)、①求点Q的坐标(用含m的式子表示);
(1)、求k的值;(2)、①求点Q的坐标(用含m的式子表示);②若 的面积大于3,直接写出点P的横坐标m的取值范围.
25. 如图, 是 的弦,C为 上一点,过点C作 的垂线与 的延长线交于点D , 连接 并延长,与 交于点E , 连接 , . (1)、求证: 是 的切线;(2)、若 ,求弦 的长.26. 在平面直角坐标系 中,抛物线 .分别过点 和点 作x轴的垂线,交抛物线于点A和点B.记抛物线在A , B之间的部分为图象G(包括A , B两点).(1)、求抛物线的顶点坐标;(2)、记图形G上任意一点的纵坐标的最大值与最小值的差为m .
(1)、求证: 是 的切线;(2)、若 ,求弦 的长.26. 在平面直角坐标系 中,抛物线 .分别过点 和点 作x轴的垂线,交抛物线于点A和点B.记抛物线在A , B之间的部分为图象G(包括A , B两点).(1)、求抛物线的顶点坐标;(2)、记图形G上任意一点的纵坐标的最大值与最小值的差为m .①当 时,若图形G为轴对称图形,求m的值;
②若存在实数t , 使得 ,直接写出a的取值范围.
27. 如图,在 中, ,作射线 , .D在射线 上,连接 ,E是 的中点,C关于点E的对称点为F , 连接 . (1)、依题意补全图形;(2)、判断 与 的数量关系并证明;(3)、平面内一点G , 使得 ,求 的值.28. 在平面直角坐标系 中,对于点A和线段 ,如果点A , O , M , N按逆时针方向排列构成菱形 ,且 ,则称线段 是点A的“ 相关线段”.例如,图1中线段 是点A的“ -相关线段”.
(1)、依题意补全图形;(2)、判断 与 的数量关系并证明;(3)、平面内一点G , 使得 ,求 的值.28. 在平面直角坐标系 中,对于点A和线段 ,如果点A , O , M , N按逆时针方向排列构成菱形 ,且 ,则称线段 是点A的“ 相关线段”.例如,图1中线段 是点A的“ -相关线段”. (1)、已知点A的坐标是 .
(1)、已知点A的坐标是 .①在图2中画出点A的“ -相关线段” ,并直接写出点M和点N的坐标;
②若点A的“ -相关线段”经过点 ,求 的值;
(2)、若存在 使得点P的“ -相关线段”和“ -相关线段”都经过点 ,记 ,直接写出t的取值范围.