北京市大兴区2021年中考数学一模试卷

试卷更新日期：2021-05-14 类型：期中考试

进入出卷网下载

一、单选题

1. 如图，是某几何体的三视图，该几何体是（）

A、圆柱 B、正方体 C、三棱柱 D、长方体

查看试题解析
2. 2021年2月25日，全国脱贫攻坚总结表彰大会在北京人民大会堂隆重举行．经过全党全国各族人民共同努力，我国脱贫攻坚战取得了全面胜利，现行标准下98990000农村贫困人口全部脱贫，832个贫困县全部摘帽，12.8万个贫困村全部出列，完成了消除绝对贫困的艰巨任务，创造了又一个彪炳史册的人间奇迹！98990000用科学记数法表示应为（）

A、 $0.9899 \times 10^{8}$ B、 $9.899 \times 10^{7}$ C、 $98.99 \times 10^{6}$ D、 $9899 \times 10^{4}$

查看试题解析
3. 勾股定理是几何学中一颗光彩夺目的明珠，现发现约有400种证明方法．下面四个图形是证明勾股定理的图形，其中既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 实数 $a ， b$ 在数轴上的对应点的位置如图所示，则下列不等关系正确的是（）

A、 $a > b$ B、 $a b > 0$ C、 $| a | > | b |$ D、 $- a < b$

查看试题解析
5. 若正多边形的一个内角是 $120 °$ ，则这个正多边形的边数为（）

A、6 B、5 C、4 D、3

查看试题解析
6. 如图， $A B$ 是 $⊙ O$ 的直径， $C ， D$ 是 $⊙ O$ 上两点，若 $∠ D = 55 °$ ，则 $∠ B O C$ 的度数是（）

A、 $35 °$ B、 $55 °$ C、 $60 °$ D、 $70 °$

查看试题解析
7. 某校进行垃圾分类的环保知识竞赛，进入决赛的共有15名学生，他们的决赛成绩如下表所示：

决赛成绩/分

100

95

90

85

人数/名

2

8

2

3

则这15名学生决赛成绩的中位数和平均数分别是（）

A、 $95, 97$ B、 $95, 93$ C、 $95, 86$ D、 $90, 95$

查看试题解析
8. 已知二次函数 $y = x^{2} + m x + n$ ，当 $x = 0$ 和 $x = 2$ 时对应的函数值相等，则下列说法中错误的是（）

A、抛物线 $y = x^{2} + m x + n$ 的开口向上 B、抛物线 $y = x^{2} + m x + n$ 与y轴有交点 C、当 $n > 1$ 时，抛物线 $y = x^{2} + m x + n$ 与x轴有交点 D、若 $P (- 1 ， y_{1}) ， Q (3 ， y_{2})$ 是抛物线 $y = x^{2} + m x + n$ 上两点，则 $y_{1} = y_{2}$

查看试题解析

二、填空题

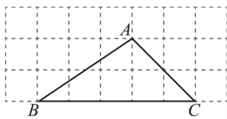
9. 若二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
10. 如图所示的网格是正方形网格， $A ， B ， C$ 是网格线的交点，则 $∠ A B C$ 与 $∠ A C B$ 的大小关系为： $∠ A B C$ $∠ A C B$ （填“>”，“=”或“<”）．

查看试题解析
11. 化简： $\frac{3 x}{x + y} + \frac{y - 2 x}{x + y} =$ ．

查看试题解析
12. 分解因式ma²﹣2mab+mb²= ．

查看试题解析
13. 某区域进行“环境改造，植树绿化”活动．若该区域种植树苗2000株，树苗的成活率为 $95 %$ ，则成活的树苗大约有株．

查看试题解析
14. 如图，在正方形 $A B C D$ 中， $E ， F$ 分别是 $A B ， A D$ 的中点，若 $E F = 2$ ，则 $A C$ 的长是．

查看试题解析
15. 小华到商店为班级购买跳绳和毽子两种体育用品，跳绳每个4元，毽子每个5元，两种体育用品共需购买22个，是否存在用90元钱完成这项购买任务的方案？（填“是”或“否”）．

查看试题解析
16. 如图，在 $▱ A B C D$ 中， $A D > A B ， E ， F$ 分别为边 $A D ， B C$ 上的点（ $E ， F$ 不与端点重合）．对于任意 $▱ A B C D$ ，下面四个结论中：

①存在无数个四边形 $A B F E$ ，使得四边形 $A B F E$ 是平行四边形；

②至少存在一个四边形 $A B F E$ ，使得四边形 $A B F E$ 菱形；

③至少存在一个四边形 $A B F E$ ，使得四边形 $A B F E$ 矩形；

④存在无数个四边形 $A B F E$ ，使得四边形 $A B F E$ 的面积是 $▱ A B C D$ 面积的一半．

所有正确结论的序号是．

查看试题解析

三、解答题

17. 计算： $2 \sin 45 ° + | - \sqrt{2} | - \sqrt{8} + {(π - 3)}^{0}$ ．

查看试题解析
18. 解不等式组： ${\begin{array}{l} \frac{x}{2} + 1 > 0, \\ 2 (x - 1) + 3 ⩾ 3 x . \end{array}$

查看试题解析
19. 已知抛物线 $y = x^{2} - 4 x + c$ 经过点(−1，8)．

(1)、求抛物线的解析式；

(2)、求抛物线与x轴交点的坐标．

查看试题解析
20. 已知 $x^{2} - 3 x - 1 = 0$ ，求代数式 $(x + 2) (x - 2) - x (3 x - 6)$ 的值．

查看试题解析
21. 已知：如图 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ．
求作：点P ，使得点P在 $A C$ 上，且点P到 $A B$ 的距离等于 $P C$ ．

作法：

①以点B为圆心，以任意长为半径作弧，分别交射线 $B A ， B C$ 于点 $D ， E$ ；

②分别以点 $D ， E$ 为圆心，以大于 $\frac{1}{2} D E$ 的长为半径作弧，两弧在 $∠ A B C$ 内部交于点F；

③作射线 $B F$ 交 $A C$ 于点P ．则点P即为所求．

(1)、使用直尺和圆规，补全图形（保留作图痕迹）；

(2)、完成下面证明．
证明：连接 $D F ， F E$ ．

在 $△ B D F$ 和 $△ B E F$ 中

${\begin{array}{l} D B = E B ， \\ D F = E F ， \\ B F = B F . \end{array}$

$∴ △ B D F ≌ △ B E F$ ．

$∴ ∠ A B F = ∠ C B F$ （）（填推理的依据）．

$∵ ∠ A C B = 90 °$ ，点P在 $A C$ 上，

$∴ P C ⊥ B C$ ．

作 $P Q ⊥ A B$ 于点Q ，

$∵$ 点P在 $B F$ 上，

$∴ P C =$ （）（填推理的依据）．

查看试题解析
22. 如图，矩形 $A B C D$ 中，对角线 $A C$ 与 $B D$ 相交于点 $O ， D E / / A C$ 交 $B C$ 的延长线于点E ．

(1)、求证： $∠ A D B = ∠ E$ ；

(2)、若AD=4，cos∠ADB= $\frac{4}{5}$ ，求 $A O$ 的长．

查看试题解析
23. 在平面直角坐标系 $x O y$ 中，直线l与双曲线 $y = \frac{m}{x}$ 交于点 $A (1 ， n)$ 和点 $B (- 2 ， - 1)$ ．

(1)、求 $m ， n$ 的值及直线l的解析式；

(2)、点 $P (x_{1} ， y_{1}) ， Q (x_{2} ， y_{2})$ 是线段 $A B$ 上两点且 $x_{1} < x_{2} ， P Q = 2 \sqrt{2}$ ，若线段 $P Q$ 与双曲线 $y = \frac{m}{x}$ 无交点，求 $x_{1}$ 的取值范围．

查看试题解析

24. 随着绿色出行意识增强，更多市民选择公共交通出行．从市交通委获悉，目前，轨道交通多条线路缩短发车间隔，保障市民出行安全、便捷．

下图是地铁10号线由西钓鱼台站开往公主坟方向，工作日和双休日的列车时刻表（列车时刻表仅供参考，实际以现场列车运行情况为准）．小明从西钓鱼台站乘10号线地铁（开往公主坟方向）出行，结合图中信息回答以下问题：

10号线西钓鱼台站列出时刻表
开往公主坟站方向工作日
5 00 06 12 18 24 30 36 40 44 48 52 56
6 00 04 08 12 16 20 24 28 32 36 41 45 47 49 51 53 55 57 59
7 01 03 05 07 09 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59
8 01 03 05 07 09 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 51 53 55 57 59
9 01 03 05 07 09 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47 49 53 57
10 01 05 09 13 17 21 25 29 33 37 41 47 53 59
11 05 11 17 24 30 36 42 48 54
12 00 07 13 19 25 31 37 43 49 56
13 02 08 14 20 26 32 39 45 51 57
14 03 09 15 21 28 34 40 46 52 58
15 04 08 11 17 23 26 29 35 41 44 47 53
16 00 03 06 12 18 21 24 30 36 40 43 46 49 52 54 57 59
17 01 03 06 05 10 12 15 17 19 21 24 26 28 31 33 35 37 40 42 44 46 49 51 53 55 58
18 00 02 05 07 09 11 14 16 18 20 23 25 27 29 32 34 36 39 41 43 45 48 50 52 54 57 59
19 01 03 06 05 10 12 15 17 19 21 24 26 31 35 40 44 49 53 58
20 02 07 11 16 21 25 30 34 39 43 48 52 57
21 01 06 10 15 19 24 29 33 38 43 48 53
22 01 09 15 24 29 39 45
5 21 表示5点21分
10号线西钓鱼台站列出时刻表
开往公主坟站方向双休日
5 00 05 15 22 29 36 43 50 57
6 04 11 18 25 32 38 45 52 59
7 03 06 13 17 21 27 34 38 42 48 52 56
8 02 09 12 16 23 26 31 37 44 49 54 59
9 04 09 13 18 23 28 33 38 43 48 53 58
10 03 08 13 18 23 28 33 38 43 48 53 58
11 03 08 14 19 25 30 36 41 47 52 58
12 03 09 14 20 25 30 36 41 47 52 58
13 03 09 14 20 25 31 36 42 47 53 58
14 04 09 15 20 26 31 37 42 48 53 59
15 04 09 15 20 26 31 37 42 48 53 59
16 04 10 15 21 26 32 37 43 48 54 59
17 05 10 16 21 27 32 38 43 49 54 59
18 05 10 16 21 27 32 38 43 49 54
19 00 06 11 16 22 27 33 38 44 49 55
20 00 06 13 20 27 34 41 46 53
21 00 07 14 21 28 35 43 50 57
22 04 11 16 25 32 39 43
5 21 表示5点21分

(1)、工作日早晨7点01分—7点59分这段时间内，列车发车间隔为分钟；

(2)、下列说法中：

①双休日早晨6点04—6点59期间列车发车最小间隔为7分钟；

②设两个相邻整点之间为一个时间段，则工作日发车次数最少的时间段是22点—23点；

③设两个相邻整点之间为一个时间段，则双休日时，每个时间段的发车次数的众数为11；

④工作日10点01分—10点59分发车次数为12．

所有正确说法的序号是；

(3)、小明周一上午乘车时间为7点—7点10分之间，周二上午乘车时间为7点—7点06分之间．若这两天发车到站的时间与图中时间表一致，用画树状图或列表的方法，求小明这两天乘坐相同车次列车的概率（每天在同一时刻发车的列车视为相同车次）？

查看试题解析

25. 如图， $A B$ 为 $⊙ O$ 的直径，点C ，点D在 $⊙ O$ 上，且点C是 $\overset{⌢}{A D}$ 的中点， $D E$ 是 $⊙ O$ 的切线且 $D E ⊥ A C$ 交 $A C$ 的延长线于点E ，连接OC．

(1)、求证： $△ A O C$ 是等边三角形；

(2)、若 $D E = 2 \sqrt{3}$ ，求 $A C$ 的长．

查看试题解析
26. 在平面直角坐标系 $x O y$ 中，抛物线 $y = x^{2} - 2 b x + b^{2} - 2 (b > 0)$ 经过点 $A (m ， n)$ ．

(1)、用含b的代数式表示抛物线顶点的坐标；

(2)、若抛物线经过点 $B (0 ， 2)$ ，且满足 $0 < m < 3$ ，求n的取值范围；

(3)、若 $3 ⩽ m ⩽ 5$ 时， $n ⩽ 2$ ，结合函数图象，直接写出b的取值范围．

查看试题解析
27. 如图，等边 $△ A B C$ 中，点P是 $B C$ 边上一点，作点C关于直线 $A P$ 的对称点D ，连接 $C D ， B D$ ，作 $A E ⊥ B D$ 于点E ．

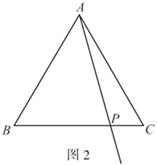(1)、若 $∠ P A C = 10 °$ ，依题意补全图1，并直接写出 $∠ B C D$ 的度数；

(2)、如图2，若 $∠ P A C = α (0 ° < α < 30 °)$ ，
①求证： $∠ B C D = ∠ B A E$ ；

②用等式表示线段 $B D ， C D ， A E$ 之间的数量关系并加以证明．

查看试题解析
28. 在平面直角坐标系 $x O y$ 中，对于任意两点 $M (x_{1} ， y_{1}) ， N (x_{2} ， y_{2})$ ，若 $| x_{1} - x_{2} | + | y_{1} - y_{2} | = k$ （k为常数且 $k \neq 0$ ），则称点M为点N的k倍直角点．
根据以上定义，解决下列问题：

(1)、已知点 $A (1 ， 1)$
①若点 $B (- 2 ， 3)$ 是点A的k倍直角点，则k的值是；

②在点 $C (2 ， 3) ， D (- 1 ， 1) ， E (0 ， - 2) ， O (0 ， 0)$ 中是点A的2倍直角点的是；

(2)、已知点 $A (1 ， 1)$ ，若直线 $y = - 2 x + b$ 上存在点A的2倍直角点，求b的取值范围；

(3)、 $⊙ T$ 的圆心T的坐标为 $(1 ， 0)$ ，半径为r ，若 $⊙ T$ 上存在点O的2倍直角点，直接写出r的取值范围．

查看试题解析

决赛成绩/分	100	95	90	85
人数/名	2	8	2	3