上海市金山区2021年中考数学二模试卷

试卷更新日期：2021-05-14 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列根式中，是最简二次根式的是（　　）

A、 $\sqrt{8}$ B、 $\sqrt{5}$ C、 $\sqrt[3]{3}$ D、 $\sqrt[4]{2}$

查看试题解析
2. 已知x＞y ，那么下列正确的是（　　）

A、x+y＞0 B、ax＞ay C、x﹣2＞y+2 D、2﹣x＜2﹣y

查看试题解析
3. 已知正比例函数 $y = kx (k \neq 0)$ 的图象经过点（1，－2），则正比例函数的解析式为（）

A、 $y = 2x$ B、 $y = - 2x$ C、 $y = \frac{1}{2} x$ D、 $y = - \frac{1}{2} x$

查看试题解析
4. 某人统计九年级一个班35人的身高时，算出平均数与中位数都是158厘米，但后来发现其中一位同学的身高记录不符合题意，将160厘米写成了166厘米，经重新计算后，正确的中位数是a厘米，那么中位数a应（　　）

A、大于158 B、小于158 C、等于158 D、无法判断

查看试题解析
5. 已知三条线段长分别为2cm、4cm、acm ，若这三条线段首尾顺次联结能围成一个三角形，那么a的取值可以是（　　）

A、1cm B、2cm C、4cm D、7cm

查看试题解析
6. 已知⊙A、⊙B、⊙C的半径分别为2、3、4，且AB＝5，AC＝6，BC＝6，那么这三个圆的位置关系（　　）．

A、⊙A与⊙B、⊙C外切，⊙B与⊙C相交 B、⊙A与⊙B、⊙C相交，⊙B与⊙C外切 C、⊙B与⊙A、⊙C外切，⊙A与⊙C相交 D、⊙B与⊙A、⊙C相交，⊙A与⊙C外切

查看试题解析

二、填空题

7. 因式分解： $x^{2} - 4 =$ .

查看试题解析
8. 已知f（x）＝ $\frac{x^{2} - 2}{x}$ ，那么f（2）＝．

查看试题解析
9. 如果反比例函数y＝ $\frac{m - 1}{x}$ （m是常数，m≠1）的图象，在每个象限内y随着x的增大而减小，那么m的取值范围是．

查看试题解析
10. 方程 $\sqrt{x + 2} = - x$ 的解是．

查看试题解析
11. 如果从方程x+1＝0，x²﹣2x﹣1＝0，x $+ \frac{1}{x} = 1 ， \sqrt{x + 1} = 0 ， x^{4} - 1 = 0 ， \sqrt{x} + \frac{1}{\sqrt{x}} = 3$ 中任意选取一个方程，那么取到的方程是整式方程的概率是．

查看试题解析
12. 关于x的方程x²﹣2x+k＝0有两个不相等的实数根，则实数k的取值范围．

查看试题解析
13. 为了了解某校初三学生在体育测试中报名球类的情况，随机调查了40名学生的报名情况，得到如下数据．

项目

排球

篮球

足球

人数

10

15

15

根据此信息，估计该校480名初三学生报名足球的学生人数约为人．

查看试题解析
14. 已知在正六边形ABCDEF中，AB＝6，那么正六边形ABCDEF的面积等于．

查看试题解析
15. 如图，BE、AD分别是△ABC的两条中线，设 $\vec{B O} = \vec{a} ， \vec{B D} = \vec{b}$ ，那么向量 $\vec{A B}$ 用向量 $\vec{a} ， \vec{b}$ 表示为．

查看试题解析
16. 小张、小王两个人从甲地出发，去8千米外的乙地，图中线段OA、PB分别反映了小张、小王步行所走的路程S（千米）与时间t（分钟）的函数关系，根据图象提供的信息，小王比小张早到乙地的时间是分钟．

查看试题解析
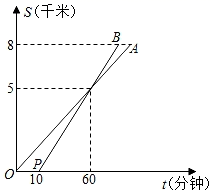17. 如图，在△ABC中，AB＝AC＝4，BC＝6，把△ABC绕着点B顺时针旋转，当点A与边BC上的点A′重合时，那么∠AA′B的余弦值等于．

查看试题解析
18. 如图，在矩形ABCD中，AB＝3，BC＝4，点E在对角线BD上，联结AE ，作EF⊥AE交边BC于F ，若BF＝ $\frac{39}{16}$ ，那么BE＝．

查看试题解析

三、解答题

19. 计算： $(\sqrt{3} - \sqrt{2}) (\sqrt{3} + \sqrt{2}) + \frac{2}{\sqrt{3} + 1} - {(\sqrt{2})}^{- 2} - | 1 - \sqrt{3} |$ ．

查看试题解析
20. 解方程组： ${\begin{matrix} 2 x - y = 1 \\ 2 x^{2} + x y - y^{2} = 5 \end{matrix}$ ．

查看试题解析
21. 如图，是一个地下排水管的横截面图，已知⊙O的半径OA等于50cm ，水的深度等于25cm（水的深度指 $\overset{⌢}{A B}$ 的中点到弦AB的距离）．
求：

(1)、水面的宽度AB ．

(2)、横截面浸没在水中的 $\overset{⌢}{A B}$ 的长（结果保留π）．

查看试题解析
22. A、B两地相距18千米，甲工程队要在A、B两地间铺设一条输送天然气的管道，乙工程队要在A、B两地间铺设一条输油管道，已知甲工程队每天比乙工程队少铺设1千米．

(1)、若两队同时开工，甲工程队每天铺设3千米，求乙工程队比甲工程队提前几天完成？

(2)、若甲工程队提前3天开工，结果两队同时完成任务，求甲、乙两队每天各铺设管道多少千米？

查看试题解析
23. 如图，已知在梯形ABCD中，AD//BC ，对角线BD平分∠ABC ，点G在底边BC上，联结DG交对角线AC于F ， ∠DGB＝∠DAB ．

(1)、求证：四边形ABGD是菱形；

(2)、联结EG ，求证：BG•EG＝BC•EF ．

查看试题解析
24. 已知直线y＝kx+b经过点A（﹣2，0），B（1，3）两点，抛物线y＝ax²﹣4ax+b与已知直线交于C、D两点（点C在点D的右侧），顶点为P ．

(1)、求直线y＝kx+b的表达式；

(2)、若抛物线的顶点不在第一象限，求a的取值范围；

(3)、若直线DP与直线AB所成的夹角等于15°，且点P在直线AB的上方，求抛物线y＝ax²﹣4ax+b的表达式．

查看试题解析
25. 已知在△ABC中，AB＝AC＝ $2 \sqrt{3}$ ，∠BAC＝120°，△ADE的顶点D在边BC上，AE交BC于点F（点F在点D的右侧），∠DAE＝30°．

(1)、求证：△ABF∽△DCA；

(2)、若AD＝ED ．
①联结EC ，当点F是BC的黄金分割点（FC＞BF）时，求 $\frac{S_{△ A B F}}{S_{△ F E C}}$ ．

②联结BE ，当DF＝1时，求BE的长．

查看试题解析

项目	排球	篮球	足球
人数	10	15	15