上海市奉贤区2021年中考数学二模试卷

试卷更新日期：2021-05-14 类型：中考模拟

进入出卷网下载

一、单选题

1. 计算3a•2a的结果是（　　）

A、6a B、6a² C、5a D、5a²

查看试题解析
2. 在下列各式中，二次根式 $\sqrt{a} + \sqrt{b}$ 的有理化因式是（）

A、 $\sqrt{a} + \sqrt{b}$ B、 $\sqrt{a} - \sqrt{b}$ C、 $\sqrt{a + b}$ D、 $\sqrt{a - b}$

查看试题解析
3. 某校对进校学生进行体温检测，在某一时段测得6名学生的体温分别为36.8℃，36.9℃，36.5℃，36.6℃，36.9℃，36.5℃，那么这6名学生体温的平均数与中位数分别是（）

A、36.7℃，36.7℃ B、36.6℃，36.8℃ C、36.8℃，36.7℃ D、36.7℃，36.8℃

查看试题解析
4. 下列函数中，y随x的增大而减小的是（）

A、 $y = 2 x$ B、 $y = \frac{2}{x}$ C、 $y = - 2 x$ D、 $y = - \frac{2}{x}$

查看试题解析
5. 如图，在梯形ABCD中，AB∥DC ，对角线AC、BD交于点O ，下列条件中，不一定能判断梯形ABCD是等腰梯形的是（）

A、AD＝BC B、∠ABC＝∠BAD C、AB＝2DC D、∠OAB＝∠OBA

查看试题解析
6. 如图，在Rt△ABC中，∠C＝90°，BC＝18，AC＝24，点O在边AB上，且BO＝2OA ．以点O为圆心，r为半径作圆，如果⊙O与Rt△ABC的边有3个公共点，那么下列各值中，半径r不可以取的是（）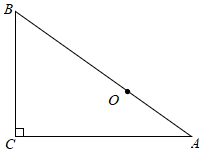

A、6 B、10 C、15 D、16

查看试题解析

二、填空题

7. 函数y= $\frac{x}{x - 1}$ 的定义域是．

查看试题解析
8. 如果抛物线y＝ax²＋bx＋c在对称轴左侧呈上升趋势，那么a的取值范围是．

查看试题解析
9. 如果一元二次方程x²﹣px＋3＝0有两个相等的实数根，那么p的值是．

查看试题解析
10. 将π， $\frac{2}{3}$ ， $\sqrt{2}$ ，0，﹣1这5个数分别写在5张相同的卡片上，字面朝下随意放在桌上，任取一张，取到无理数的概率为．

查看试题解析
11. 某小区一天收集各类垃圾共2.4吨，绘制成各类垃圾收集量的扇形图，其中湿垃圾在扇形图中对应的圆心角为135°，那么该小区这一天湿垃圾共收集了吨．

查看试题解析
12. 某品牌汽车公司大力推进技术革新，新款汽车油耗从每百公里8升下降到每百公里6.8升，那么该汽车油耗的下降率为．

查看试题解析
13. 如图△ABC中，点D在BC上，且CD＝2BD ．设 $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ，那么 $\vec{A D}$ ＝

查看试题解析
14. 已知传送带和水平面所成斜坡的坡度i＝1：3，如果物体在传送带上经过的路程是30米，那么该物体上升的高度是米（结果保留根号）．

查看试题解析
15. 如图，⊙O的半径为6，如果弦AB是⊙O内接正方形的一边，弦AC是⊙O内接正十二边形的一边，那么弦BC的长为．

查看试题解析
16. 我们把反比例函数图象上到原点距离相等的点叫做反比例函数图象上的等距点．如果第一象限内点A（2，4）与点B是某反比例函数图象上的等距点，那么点A、B之间的距离是．

查看试题解析
17. 如图，在△ABC中，AD是BC边上的中线，∠ADC＝60°，BC＝3AD ．将△ABD沿直线AD翻折，点B落在平面上的B′处，联结AB′交BC于点E ，那么 $\frac{C E}{B E}$ 的值为．

查看试题解析

三、解答题

18. 先化简，再求值： $\frac{4 x}{x^{2} - 2 x - 3} - \frac{x}{x - 3} + \frac{2 x}{x + 1}$ ，其中 $x = \sqrt{3}$ ．

查看试题解析
19. 解不等式组： ${\begin{matrix} \frac{1}{2} x - 3 < 2 x \\ \frac{2 x - 1}{3} \leq \frac{x + 1}{2} \end{matrix}$ ，并把解集在数轴上表示出来．

查看试题解析
20. 如图，已知，在Rt△ABC中，∠C＝90°，AB＝4，BC＝2，点D是AC的中点，联结BD并延长至点E ，使∠E＝∠BAC ．

(1)、求sin∠ABE的值；

(2)、求点E到直线BC的距离．

查看试题解析
21. 为了预防“诺如病毒”，某校对专用教室采取“药熏”消毒．从开始消毒到结束，室内含药量y（毫克/立方米）与时间x（分）这两个变量之间的关系如图中折线OA﹣AB所示．

(1)、求20分钟至60分钟时间段之间的含药量y与时间x的函数解析式（不要求写定义域）；

(2)、开始消毒后，消毒人员在某一时刻对该专用教室的含药量进行第一次检测，时隔半小时进行了第二次跟踪检测，发现室内含药量比第一次检测时的含药量下降了2毫克/立方米，求第一次检测时的含药量．

查看试题解析
22. 如图，已知，在平行四边形ABCD中，E为射线CB上一点，联结DE交对角线AC于点F ， ∠ADE＝∠BAC ．

(1)、求证：CF•CA＝CB•CE；

(2)、如果AC＝DE ，求证：四边形ABCD是菱形．

查看试题解析
23. 如图，在平面直角坐标系xOy中，已知B（0，2），C（1，﹣ $\frac{3}{2}$ ），点A在x轴正半轴上，且OA＝2OB ，抛物线y＝ax²＋bx（a≠0）经过点A、C ．

(1)、求这条抛物线的表达式；

(2)、将抛物线先向右平移m个单位，再向上平移1个单位，此时点C恰好落在直线AB上的点C′处，求m的值；

(3)、设点B关于原抛物线对称轴的对称点为B′，联结AC ，如果点F在直线AB′上，∠ACF＝∠BAO ，求点F的坐标．

查看试题解析
24. 如图，已知扇形AOB的半径OA＝4，∠AOB＝90°，点C、D分别在半径OA、OB上（点C不与点A重合），联结CD ．点P是弧AB上一点，PC＝PD ．

(1)、当cot∠ODC＝ $\frac{3}{4}$ ，以CD为半径的圆D与圆O相切时，求CD的长；

(2)、当点D与点B重合，点P为弧AB的中点时，求∠OCD的度数；

(3)、如果OC＝2，且四边形ODPC是梯形，求 $\frac{S_{Δ P C D}}{S_{Δ O C D}}$ 的值．

查看试题解析