湘教版备考2021年中考数学三轮复习专题6反比例函数
试卷更新日期:2021-05-14 类型:三轮冲刺
一、单选题
-
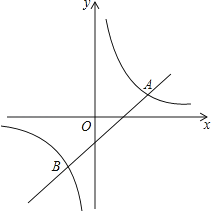
1. 如图,点A是反比例图数y= (x<0)图象上一点,AC⊥x轴于点C,与反比例函数y= (x<0)图象交于点B,AB=2BC,连接OA、OB,若△OAB的面积为3,则m+n=( )
 A、﹣4 B、﹣6 C、﹣8 D、﹣122. 如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为6,则k1﹣k2的值为( )
A、﹣4 B、﹣6 C、﹣8 D、﹣122. 如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为6,则k1﹣k2的值为( ) A、12 B、﹣12 C、6 D、﹣63. 在平面直角坐标系xOy中,过点A(1,6)的直线与反比例函数 的图象的另一个交点为B,与x轴交于点P,若AP=2PB,则点P的坐标是( )A、(1,0) B、(3,0) C、(﹣1,0) D、(3,0)或(﹣1,0)4. 如图所示,在直角平面坐标系Oxy中,点A、B、C为反比例函数y= (k>0)上不同的三点,连接OA、OB、OC , 过点A作AD⊥y轴于点D , 过点B、C分别作BE , CF垂直x轴于点E、F , OC与BE相交于点M , 记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3 , 则( )
A、12 B、﹣12 C、6 D、﹣63. 在平面直角坐标系xOy中,过点A(1,6)的直线与反比例函数 的图象的另一个交点为B,与x轴交于点P,若AP=2PB,则点P的坐标是( )A、(1,0) B、(3,0) C、(﹣1,0) D、(3,0)或(﹣1,0)4. 如图所示,在直角平面坐标系Oxy中,点A、B、C为反比例函数y= (k>0)上不同的三点,连接OA、OB、OC , 过点A作AD⊥y轴于点D , 过点B、C分别作BE , CF垂直x轴于点E、F , OC与BE相交于点M , 记△AOD、△BOM、四边形CMEF的面积分别为S1、S2、S3 , 则( ) A、S1=S2+S3 B、S1>S2=S3 C、S3>S2>S1 D、S1S2<S325. 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线 与正方形ABCD有公共点,则k的取值范围为( )
A、S1=S2+S3 B、S1>S2=S3 C、S3>S2>S1 D、S1S2<S325. 如图,正方形ABCD位于第一象限,边长为3,点A在直线y=x上,点A的横坐标为1,正方形ABCD的边分别平行于x轴、y轴.若双曲线 与正方形ABCD有公共点,则k的取值范围为( ) A、1<k<9 B、2≤k≤34 C、1≤k≤16 D、4≤k<166. 已知某函数的图象C与函数y= 的图象关于直线y=2对称下列命题:①图象C与函数y= 的象交于点( ,2);②( ,-2)在图象C上;③图象C上的点的纵坐标都小于4;④A(x1 , y1),B(x2 , y2)是图象C上任意两点,若x1>x2 , 则y1-y2 , 其中真命题是( )A、①② B、①③④ C、②③④ D、①②③④7. 如图,已知A , B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C , 动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C , 过P作PM⊥x轴,垂足为M . 设三角形OMP的面积为S , P点运动时间为t , 则S关于t的函数图象大致为( )
A、1<k<9 B、2≤k≤34 C、1≤k≤16 D、4≤k<166. 已知某函数的图象C与函数y= 的图象关于直线y=2对称下列命题:①图象C与函数y= 的象交于点( ,2);②( ,-2)在图象C上;③图象C上的点的纵坐标都小于4;④A(x1 , y1),B(x2 , y2)是图象C上任意两点,若x1>x2 , 则y1-y2 , 其中真命题是( )A、①② B、①③④ C、②③④ D、①②③④7. 如图,已知A , B是反比例函数y= (k>0,x>0)图象上的两点,BC∥x轴,交y轴于点C , 动点P从坐标原点O出发,沿O→A→B→C(图中“→”所示路线)匀速运动,终点为C , 过P作PM⊥x轴,垂足为M . 设三角形OMP的面积为S , P点运动时间为t , 则S关于t的函数图象大致为( )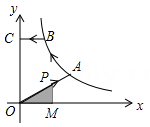 A、
A、 B、
B、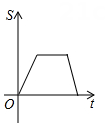 C、
C、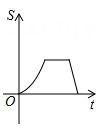 D、
D、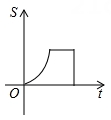 8. 如图所示双曲线y= 与y=﹣ 分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣ 上的点,C是y= 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y= 在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3, );③k=4;④△ABC的面积为定值7,正确的有( )
8. 如图所示双曲线y= 与y=﹣ 分别位于第三象限和第二象限,A是y轴上任意一点,B是y=﹣ 上的点,C是y= 上的点,线段BC⊥x轴于D,且4BD=3CD,则下列说法:①双曲线y= 在每个象限内,y随x的增大而减小;②若点B的横坐标为﹣3,则C点的坐标为(﹣3, );③k=4;④△ABC的面积为定值7,正确的有( ) A、1个 B、2个 C、3个 D、4个9. 如图,平行于x轴的直线与函数 (k1>0,x>0),y=(k2>0,x>0)的图像分别交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为( )
A、1个 B、2个 C、3个 D、4个9. 如图,平行于x轴的直线与函数 (k1>0,x>0),y=(k2>0,x>0)的图像分别交于A,B两点,点A在点B的右侧,C为x轴上的一个动点.若△ABC的面积为4,则k1-k2的值为( )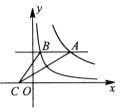 A、8 B、-8 C、4 D、-410. 反比例函数y= 的图象向右平移 个单位长度得到一个新的函数,当自变量x取1,2,3,4,5,…,(正整数)时,新的函数值分别为y1 , y2 , y3 , y4 , y5 , …,其中最小值和最大值分别为( )A、y1 , y2 B、y43 , y44 C、y44 , y45 D、y2014 , y201511. 如图,已知点 A 、B分别在反比例函数 的图象上,且OA ⊥OB ,则 的值为( )
A、8 B、-8 C、4 D、-410. 反比例函数y= 的图象向右平移 个单位长度得到一个新的函数,当自变量x取1,2,3,4,5,…,(正整数)时,新的函数值分别为y1 , y2 , y3 , y4 , y5 , …,其中最小值和最大值分别为( )A、y1 , y2 B、y43 , y44 C、y44 , y45 D、y2014 , y201511. 如图,已知点 A 、B分别在反比例函数 的图象上,且OA ⊥OB ,则 的值为( )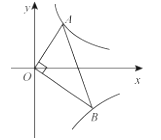 A、 B、2 C、 D、412. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
A、 B、2 C、 D、412. 教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:45)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )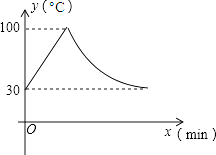 A、7:20 B、7:30 C、7:45 D、7:50
A、7:20 B、7:30 C、7:45 D、7:50二、填空题
-
13. 如图,把一块含30°角的三角板的直角顶点放在反比例函数y=- (x<0)的图象上的点C处,另两个顶点分别落在原点O和x轴的负半轴上的点A处,且∠CAO=30°,则AC边与该函数图象的另一交点D的坐标为 .
 14. 如图,在平面直角坐标系 中, , ,双曲线 与线段 无公共点,则 的取值范围是 .
14. 如图,在平面直角坐标系 中, , ,双曲线 与线段 无公共点,则 的取值范围是 .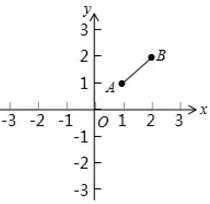 15. 如图,一次函数 分别与x,y轴交于点N,M,与反比例函数 (x>0)的图象交于点A,若点M把AN分成2:3两部分时,则 .
15. 如图,一次函数 分别与x,y轴交于点N,M,与反比例函数 (x>0)的图象交于点A,若点M把AN分成2:3两部分时,则 . 16. 如图,曲线 是双曲线 绕原点O逆时针旋转 得到的图形,P是双曲线 上任意一点,点A在直线 上,且 ,则 的面积等于
16. 如图,曲线 是双曲线 绕原点O逆时针旋转 得到的图形,P是双曲线 上任意一点,点A在直线 上,且 ,则 的面积等于 17. 如图,已知点A,C在反比例函数 的图象上,点B,D在反比例函 的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=5,CD=4,AB与CD的距离为6,则a−b的值是.
17. 如图,已知点A,C在反比例函数 的图象上,点B,D在反比例函 的图象上,AB∥CD∥x轴,AB,CD在x轴的两侧,AB=5,CD=4,AB与CD的距离为6,则a−b的值是. 18. 如图,已知在平面直角坐标系xOy中,直线 分别交x轴,y轴于点A和点B,分别交反比例函数 , 的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC,OD. 若△COE的面积与△DOB的面积相等,则k的值是.
18. 如图,已知在平面直角坐标系xOy中,直线 分别交x轴,y轴于点A和点B,分别交反比例函数 , 的图象于点C和点D,过点C作CE⊥x轴于点E,连结OC,OD. 若△COE的面积与△DOB的面积相等,则k的值是.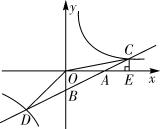 19. 直角坐标系中△OAB , △BCD均为等腰直角三角形,OA=AB , BD=CD , 点A在x轴的正半轴上,点D在AB上,△OAB与△BCD的面积之差为3,反比例函数y= 的图象经过点C , 则k的值为 .
19. 直角坐标系中△OAB , △BCD均为等腰直角三角形,OA=AB , BD=CD , 点A在x轴的正半轴上,点D在AB上,△OAB与△BCD的面积之差为3,反比例函数y= 的图象经过点C , 则k的值为 . 20. 如图,点P1(x1 , y1),点P2(x2 , y2),…,点Pn(xn , yn)在函数y= (x>0)的图象上,△P1OA,△P2A1A2 , △P3A2A3 , …,△PnAn﹣1An都是等腰直角三角形,斜边OA1 , A1A2 , A2A3 , …,An﹣1An都在x轴上(n是大于或等于2的正整数).若△P1OA1的内接正方形B1C1D1E1的周长记为l1 , △P2A1A2的内接正方形的周长记为l2 , …,△PnAn﹣1An的内接正方形BnCnDnEn的周长记为ln , 则l1+l2+l3+…+ln=(用含n的式子表示).
20. 如图,点P1(x1 , y1),点P2(x2 , y2),…,点Pn(xn , yn)在函数y= (x>0)的图象上,△P1OA,△P2A1A2 , △P3A2A3 , …,△PnAn﹣1An都是等腰直角三角形,斜边OA1 , A1A2 , A2A3 , …,An﹣1An都在x轴上(n是大于或等于2的正整数).若△P1OA1的内接正方形B1C1D1E1的周长记为l1 , △P2A1A2的内接正方形的周长记为l2 , …,△PnAn﹣1An的内接正方形BnCnDnEn的周长记为ln , 则l1+l2+l3+…+ln=(用含n的式子表示).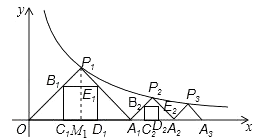 21. 如图,点 为直线 上的两点,过 两点分别作y轴的平行线交双曲线 ( )于 两点. 若 ,则 的值为.
21. 如图,点 为直线 上的两点,过 两点分别作y轴的平行线交双曲线 ( )于 两点. 若 ,则 的值为.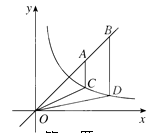
三、解答题
-
22. 如图,点A为函数 图象上一点,连结OA,交函数 的图象于点B,点C是x轴上一点,且AO=AC,求△ABC的面积.
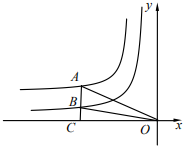
 23. 如图,直线AB交双曲线 于A,B两点,交x轴于点C,且BC= AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少?
23. 如图,直线AB交双曲线 于A,B两点,交x轴于点C,且BC= AB,过点B作BM⊥x轴于点M,连结OA,若OM=3MC,S△OAC=8,则k的值为多少? 24. 已知反比例函数y= (k为常数,k≠1).
24. 已知反比例函数y= (k为常数,k≠1).(Ⅰ)其图象与正比例函数y=x的图象的一个交点为P,若点P的纵坐标是2,求k的值;
(Ⅱ)若在其图象的每一支上,y随x的增大而减小,求k的取值范围;
(Ⅲ)若其图象的一支位于第二象限,在这一支上任取两点A(x1 , y1)、B(x2 , y2),当y1>y2时,试比较x1与x2的大小.
25. 已知实数a , b满足a-b=1,a2-ab+2>0,当1≤x≤2时,函数y= (a≠0)的最大值与最小值之差是1,求a的值26. 如图,一次函数y=kx+b的图象与x轴交于点A,与反比例函数y= (x>0)的图象交于点B(2,n),过点B作BC⊥x轴于点C,点P(3n﹣4,1)是该反比例函数图象上的一点,且∠PBC=∠ABC,求反比例函数和一次函数的表达式.
四、作图题
-
27. 已知反比例函数 的图象与正比例函数 的图象交于点 ,求这个反比例函数的表达式,并在同一平面直角坐标系内,画出这两个函数的图象.28. 在初中阶段的函数学习中,我们经历了“确定函数的表达式——利用函数图象研究其性质——运用函数解决问题”的学习过程,在画函数图象时,我们能通过描点或平移的方法画出函数图象.结合上面经历的学习过程,现在来解决下面的问题;
在函数 中,当 时, .
 (1)、求这个函数的表达式;(2)、在给出的平面直角坐标系中,用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质;(3)、已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.29. 在函数的学习中,我们经历了“确定函数表达式——画函数图象——利用函数图象研究函数性质——利用图像解决问题”的学习过程.我们可以借鉴这种方法探究函数 的图像性质.
(1)、求这个函数的表达式;(2)、在给出的平面直角坐标系中,用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质;(3)、已知函数 的图象如图所示,结合你所画的函数图象,直接写出不等式 的解集.29. 在函数的学习中,我们经历了“确定函数表达式——画函数图象——利用函数图象研究函数性质——利用图像解决问题”的学习过程.我们可以借鉴这种方法探究函数 的图像性质. (1)、补充表格,并画出函数的图象
(1)、补充表格,并画出函数的图象①列表:
x
…
-3
-1
0
2
3
5
…
y
…
-1
-2
-4
4
1
…
②描点并连线,画图.
(2)、观察图像,写出该函数图象的一个增减性特征:;(3)、函数 的图像是由函数 的图像如何平移得到的? , 其对称中心的坐标为;(4)、根据上述经验,猜一猜函数 的图像大致位置,结合图像直接写出y≥3时,x的取值范围.30. 模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下: (1)、建立函数模型
(1)、建立函数模型设矩形相邻两边的长分别为x,y,由矩形的面积为4,得 ,即 ;由周长为m,得 ,即 .满足要求的 应是两个函数图象在第象限内交点的坐标.
(2)、画出函数图象函数 的图象如图所示,而函数 的图象可由直线 平移得到.请在同一直角坐标系中直接画出直线 .
(3)、平移直线 ,观察函数图象①当直线平移到与函数 的图象有唯一交点 时,求周长m的值;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)、得出结论若能生产出面积为4的矩形模具,则周长m的取值范围为.
31. 参照学习函数的过程方法,探究函数 的图像与性质,因为 ,即 ,所以我们对比函数 来探究列表:…
-4
-3
-2
-1
1
2
3
4
…
…
1
2
4
-4
-2
-1
…
…
2
3
5
-3
-2
0
…
描点:在平面直角坐标系中以自变量 的取值为横坐标,以 相应的函数值为纵坐标,描出相应的点如图所示:
 (1)、请把 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;(2)、观察图象并分析表格,回答下列问题:
(1)、请把 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;(2)、观察图象并分析表格,回答下列问题:①当 时, 随 的增大而;(“增大”或“减小”)
② 的图象是由 的图象向平移个单位而得到的;
③图象关于点中心对称.(填点的坐标)
(3)、函数 与直线 交于点A,B,求 的面积.32. 如图,点 在反比例函数 的图象在第二象限内的分支上, 轴于点 , 是原点,且 的面积为 .试解答下列问题: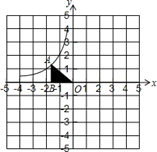 (1)、比例系数 ;(2)、在给定直角坐标系中,画出这个函数图象的另一个分支;(3)、当 时,写出 的取值范围.
(1)、比例系数 ;(2)、在给定直角坐标系中,画出这个函数图象的另一个分支;(3)、当 时,写出 的取值范围.五、综合题
-
33. 如图,已知函数 的图象与一次函数 的图象相交不同的点A、B,过点A作AD⊥ 轴于点D,连接AO,其中点A的横坐标为 ,△AOD的面积为2.
 (1)、求 的值及 =4时 的值;(2)、记 表示为不超过 的最大整数,例如: , ,设 ,若 ,求 值34. 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5.
(1)、求 的值及 =4时 的值;(2)、记 表示为不超过 的最大整数,例如: , ,设 ,若 ,求 值34. 如图,点A(m,6)、B(n,1)在反比例函数图象上,AD⊥x轴于点D,BC⊥x轴于点C,DC=5. (1)、求m、n的值并写出该反比例函数的解析式.(2)、点E在线段CD上,S△ABE=10,求点E的坐标.35. 如图,在矩形 OABC中,OA=3,OC=5,分别以 OA、OC所在直线为x 轴、y 轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=(k>0)的图象经过点D且与边BA交于点E,连接DE.
(1)、求m、n的值并写出该反比例函数的解析式.(2)、点E在线段CD上,S△ABE=10,求点E的坐标.35. 如图,在矩形 OABC中,OA=3,OC=5,分别以 OA、OC所在直线为x 轴、y 轴,建立平面直角坐标系,D是边CB上的一个动点(不与C、B重合),反比例函数y=(k>0)的图象经过点D且与边BA交于点E,连接DE. (1)、连接OE,若△EOA的面积为2,则k=(2)、连接CA,DE与CA是否平行?请说明理由:
(1)、连接OE,若△EOA的面积为2,则k=(2)、连接CA,DE与CA是否平行?请说明理由:
(3)、是否存在点D,使得点B关于DE的对称点在OC上?若存在,求出点D的坐标;若不存在,请说明理由:
36. 如图,已知反比例函数y=与一次函数y=x+b的图象在第一象限相交于点A(1,﹣k+4). (1)、试确定这两个函数的表达式:
(1)、试确定这两个函数的表达式:
(2)、求出这两个函数图象的另一个交点B的坐标,并求△A0B的面积: