河南省驻马店市遂平县2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2021-05-13 类型：期中考试

进入出卷网下载

一、单选题

1. 如果x=2是方程 $\frac{1}{2}$ x+a=﹣1的解，那么a的值是（）

A、0 B、2 C、﹣2 D、﹣6

查看试题解析
2. 根据等式性质，下列结论正确的是（）

A、如果 $- 2 a = 2 b$ ，那么 $a = - b$ B、如果 $a - 2 = 2 - b$ ，那么 $a = - b$ C、如果 $2 a = b - 2$ ，那么 $a = b$ D、如果 $2 a = \frac{1}{2} b$ ，那么 $a = b$

查看试题解析
3. 如图，下列四个天平中，相同形状的物体的重量是相等的，其中第①个天平是平衡的，根据第①个天平，后三个天平中不平衡的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
4. 在如图所示的2018年1月的月历表中，任意框出表中竖列上的三个相邻的数，这三个数的和不可能是（）

A、27 B、51 C、65 D、72

查看试题解析
5. 若关于x，y的方程组 ${\begin{array}{l} 2 x + y = 4 \\ x + 2 y = - 3 m + 2 \end{array}$ 的解满足 $x - y > - \frac{3}{2}$ ，则m的最小整数解为（）

A、﹣3 B、﹣2 C、﹣1 D、0

查看试题解析
6. 某种商品的进价为800元，出售时标价为1200元，后来由于该商品积压，商店准备打折销售，但要保证利润率不低于5%，则至多可打（　　）

A、6折 B、7折 C、8折 D、9折

查看试题解析
7. 某校运动员分组训练，若每组7人，则余3人:若每组8人，则缺5人.设运动员人数为x人，组数为y组，则可列方程为（）

A、 ${\begin{array}{l} 7 y = x + 3 \\ 8 y = x + 5 \end{array}$ B、 ${\begin{array}{l} 7 y = x + 3 \\ 8 y + 5 = x \end{array}$ C、 ${\begin{array}{l} 7 y = x - 3 \\ 8 y + 5 = x \end{array}$ D、 ${\begin{array}{l} 7 y = x - 3 \\ 8 y = x + 5 \end{array}$

查看试题解析
8. 已知关于x、y的二元一次方程组 $\{\begin{matrix} 3 x + 5 y = 6 \\ 3 x + k y = 10 \end{matrix}$ 给出下列结论：①当k=5时，此方程组无解；②若此方程组的解也是方程6x+15y=16的解，则k=10；③无论整数k取何值，此方程组一定无整数解（x、y均为整数），其中正确的是（　　）

A、①②③ B、①③ C、②③ D、①②

查看试题解析
9. 我国古代名著 $《$ 九章算术 $》$ 中有一题：“今有凫起南海，七日至北海，雁起北海，九日至南海 $.$ 今凫雁俱起，问何日相逢？”意思是：野鸭从南海起飞到到北海需要7天；大雁从北海飞到南海需要9天 $.$ 野鸭和大雁同时分别从南海和北海出发，多少天相遇？设野鸭与大雁从南海和北海同时起飞，经过x天相遇，可列方程为 $($ $)$

A、 $9 x - 7 x = 1$ B、 $9 x + 7 x + 1$ C、 $\frac{1}{7} x + \frac{1}{9} x = 1$ D、 $\frac{1}{7} x - \frac{1}{9} x = 1$

查看试题解析
10. 关于x的不等式组 ${\begin{array}{l} \frac{x + 15}{2} > x - 3 \\ \frac{2 x + 2}{3} < x + a \end{array}$ 只有4个整数解，则a的取值范围是（）

A、 $- 5 \leq a \leq - \frac{14}{3}$ B、 $- 5 \leq a < - \frac{14}{3}$ C、 $- 5 < a \leq - \frac{14}{3}$ D、 $- 5 < a < - \frac{14}{3}$

查看试题解析

二、填空题

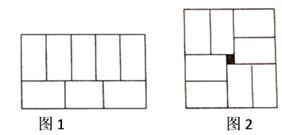
11. 方程 $2 x - 1 = 0$ 的解是.

查看试题解析
12. 若关于x的方程5x﹣1=2x+a的解与方程4x+3=7的解相同，则a= ．

查看试题解析
13. 若关于x、y的二元一次方程组 ${\begin{matrix} x - y = 2 m + 1 \\ x + 3 y = 3 \end{matrix}$ 的解满足x+y＞0，则m的取值范围是．

查看试题解析
14. 小明在拼图时，发现 $8$ 个样大小的长方形，恰好可以拼成一个大的长方形如图（1）；小红看见了，说：“我也来试试.”结果小红七拼八凑，拼成了如图（2）那样的正方形，中间还留下了一个洞，恰好是边长为 $5 m m$ 的小正方形，则每个小长方形的面积为 $m m^{2}$ .

查看试题解析
15. 一列方程如下排列：
$\frac{x}{4} + \frac{x - 1}{2} = 1$ 的解是 $x = 2$ ，

$\frac{x}{6} + \frac{x - 2}{2} = 1$ 的解是 $x = 3$ ，

$\frac{x}{8} + \frac{x - 3}{2} = 1$ 的解是 $x = 4$ ，

……

根据观察得到的规律，写出其中解是 $x = 2020$ 的方程。

查看试题解析

三、解答题

16. $\frac{4 x - 1.5}{0.5} - \frac{5 x - 0.8}{0.2} = \frac{1.2 - x}{0.1} + 3$ .

查看试题解析
17. 解方程组： ${\begin{array}{l} \frac{2 x - 1}{5} + \frac{0.3 y - 0.2}{0.4} = 2 \\ \frac{3 x + 1}{5} - \frac{0.03 y + 0.02}{0.04} = 0 \end{array}$ .

查看试题解析
18. 解不等式 $\frac{2 x + 3}{5} - 2 > \frac{x + 1}{4}$ （在数轴上把解集表示出来）

查看试题解析
19. 解不等式组 ${\begin{matrix} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 2 \\ 5 x - 1 < 3 (x + 1) \end{matrix}$ 并将解集在数轴上表示出来.

查看试题解析
20. 阅读理解：
我们把 $| \begin{array}{l} a \\ c \end{array} \begin{array}{l} b \\ d \end{array} |$ 称作二阶行列式，规定它的运算法则为 $| \begin{array}{l} a \\ c \end{array} \begin{array}{l} b \\ d \end{array} |$ ＝ad﹣bc，如 $| \begin{array}{l} 2 \\ 4 \end{array} \begin{array}{l} 3 \\ 5 \end{array} |$ ＝2×5﹣3×4＝﹣2.如果有 $| \begin{array}{l} 2 \\ 1 \end{array} \begin{array}{l} 3 - x \\ x \end{array} |$ ＞0，求x的解集，并将解集在数轴上表示出来.

查看试题解析
21. 某工厂现有甲种原料 $280 k g$ ，乙种原料 $190 k g$ ，计划用这两种原料生产 $A, B$ 两种产品50件，已知生产一件 $A$ 产品需甲种原料 $7 k g$ 、乙种原料 $3 k g$ ，可获利400元；生产一件B产品需甲种原料 $3 k g$ ，乙种原料 $5 k g$ ，可获利350元．

(1)、请问工厂有哪几种生产方案？

(2)、选择哪种方案可获利最大，最大利润是多少？

查看试题解析
22. 阅读以下结论：
（ 1 ）若|x|＝a（a≥0），则x＝±a.

（ 2 ）若|x|＞a（a＞0），则x＞a或x＜﹣a；

若|x|＜a（a＞0），则﹣a＜x＜a.

（ 3 ）若（x﹣a）（x﹣b）＞0（0＜a＜b），则x＞b或x＜a；

若（x﹣a）（x﹣b）＜0（0＜a＜b），则a＜x＜b.

根据上述结论，解答下面问题：

(1)、解方程：|3x﹣2|﹣4＝0.

(2)、解不等式：|3x﹣2|﹣4＞0.

(3)、解不等式：|3x﹣2|﹣4＜0.

(4)、解不等式：（x﹣2）（x﹣5）＞0.

(5)、解不等式：（2x﹣3）（2x﹣5）＜0.

查看试题解析
23. 为加强中小学生安全和禁毒教育，某校组织了“防溺水、交通安全、禁毒”知识竞赛，为奖励在竞赛中表现优异的班级，学校准备从体育用品商场一次性购买若干个足球和篮球（每个足球的价格相同，每个篮球的价格相同），购买1个足球和1个篮球共需159元；足球单价是篮球单价的2倍少9元．

(1)、求足球和篮球的单价各是多少元？

(2)、根据学校实际情况，需一次性购买足球和篮球共20个，但要求购买足球和篮球的总费用不超过1550元，学校最多可以购买多少个足球？

查看试题解析