河南省周口市西华县2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期：2021-05-13 类型：期中考试
一、单选题
-
1. 的平方根是（ ）A、 B、 C、±2 D、22. 下列各数中，是无理数的是（ ）A、1.3 B、 C、 D、π+13. 在平面直角坐标系中，将点A（﹣2，﹣2）先向右平移6个单位长度再向上平移5个单位长度得到点A'，则点A'的坐标是（ ）A、（4，5） B、（4，3） C、（6，3） D、（﹣8，﹣7）4. 下列命题是真命题的是（ ）A、垂直于同一条直线的两条直线平行 B、相等的角是对顶角 C、平行于同一条直线的两条直线平行 D、内错角相等5. 如图，直线AB，CD被直线EF所截，与AB，CD分别交于点E，F，下列描述：
①∠1和∠2互为同位角 ②∠3和∠4互为内错角
③∠1=∠4 ④∠4+∠5=180°
其中，正确的是（ ）
A、①③ B、②④ C、②③ D、③④6. 下列命题是假命题的是（ ）A、0的平方根是0 B、无限小数都是无理数 C、算术平方根最小的数是0 D、最大的负整数是﹣17. 一个长方形在平面直角坐标系中三个顶点的坐标分别是（﹣1，﹣1）、（﹣1，2）、（3，2），则第四个顶点的坐标是（ ）A、（2，2） B、（2，3） C、（3，﹣1） D、（3，3）8. 如图，已知AB∥CD，∠A＝120°，∠C＝130°，那么∠APC的度数是（ ）
A、100° B、110° C、120° D、130°9. 点P到x轴的距离是2，到y轴的距离是3，且点P在y轴的右侧，则P点的坐标是（ ）A、（2，3） B、（3，2）或（3，﹣2） C、（3，2） D、（2，3）或（2，﹣3）10. 下列说法正确的是（ ）A、若ab＝0，则点P（a，b）表示原点 B、点（2，a）在第三象限 C、若点A、B的坐标分别是（2，﹣2）、（2，2），则直线AB∥x轴 D、若ab＞0，则点P（a，b）在第一或第三象限二、填空题
-
11. 如果x2＝3，则x＝ ．12. 一个数的立方等于它本身，这个数是13. 已知点M在y轴上，纵坐标为4，点P（6，﹣4），则△OMP的面积是.14. 在平面直角坐标系中，有点A（a﹣2，a），过点A作AB⊥x轴，交x轴于点B ， 且AB＝2，则点A的坐标是 ．15. 如图所示，直线AB，BC，AC两两相交，交点分别为A，B，C，点D在直线AB上，过点D作DE∥BC交直线AC于点E，过点E作EF∥AB交直线BC于点F，若∠ABC＝50°，则∠DEF的度数.
三、解答题
-
16. 计算：(1)、|﹣5|+ + ；(2)、 .17. 求下列各式中的x值：(1)、（x﹣1）2＝4；(2)、（2x+1）3+64＝0；(3)、x3﹣3＝ .18. 已知实数a+9的一个平方根是﹣5，2b﹣a的立方根是﹣2，求 +2 的算术平方根.19. 如图所示，四边形ABCD中，AE平分∠DAB，AE∥CF，∠B＝∠D＝90°.求证：CF平分∠BCD.
20. 如图，在平面直角坐标系xOy中，A、B、C三点的坐标分别为（﹣5，4）、（﹣3，0）、（0，2）.
(1)、画出三角形ABC，并求其面积；(2)、如图，△A′B′C′是由△ABC经过怎样的平移得到的？(3)、已知点P（a，b）为△ABC内的一点，则点P在△A′B′C′内的对应点P′的坐标（ ， ）.21. 如图所示，已知AB∥CD，直线EF分别交AB、CD于E、F两点，FG平分∠EFD，交AB于点G.若∠1＝52°，求∠BGF的度数.
22. 已知点P（2x﹣6，3x＋1），求下列情形下点P的坐标.(1)、点P在y轴上；(2)、点P到x轴、y轴的距离相等，且点P在第二象限；(3)、点P在过点A（2，﹣4）且与y轴平行的直线上.23. 如图所示，直线AB∥CD，直线EF分别交AB、CD于E、F两点，∠BEF、∠DFE的平分线相交于点K.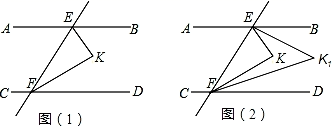
(1)、求∠EKF的度数；(2)、如图（2）所示，作∠BEK、∠DFK的平分线相交于点K1 ， 问∠K1与∠K的度数是否存在某种特定的等量关系？写出结论并证明.(3)、在图（2）中作∠BEK1、∠DFK1的平分线相交于点K2 ， 作∠BEK2、∠DFK2的平分线相交于点K3 ， 依此类推，……，请直接写出∠K4的度数.