河南省信阳市潢川县2019-2020学年七年级下学期数学期中考试试卷（A卷）
试卷更新日期：2021-05-13 类型：期中考试
一、单选题
-
1. 下列实数是无理数的是（ ）A、 B、﹣1 C、 D、3.142. 点P（-3，2）位于（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 若一个数的平方等于6，则这个数等于（ ）A、36 B、 C、± D、34. 下列命题中，是假命题的是（ ）A、两点之间，线段最短 B、同旁内角互补 C、直角的补角仍然是直角 D、垂线段最短5. 下列计算正确的是（ ）A、 =3 B、 =±2 C、 =﹣7 D、6. 如图，AD∥BC，∠B=30°，DB平分∠ADE，则∠DEC的度数为（ ）
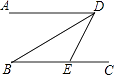A、30° B、60° C、90° D、120°7. 如图，在一次活动中，位于 处的七年一班准备前往相距 的 处与七年二班会合，若用方向和距离描述七年二班相对于七年一班的位置，可以描述为（ ）
A、南偏西40°，3km B、南偏西50°，3km C、北偏东40°，3km D、北偏东50°，3km8. 如图，现将一块含有60°角的三角板的顶点放在直尺的一边上，若∠2=50°，那么∠1的度数为（ ）
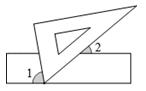A、50° B、60° C、70° D、80°9. 已知点A(2，1)，过点A作x轴的垂线，垂足为C，则点C的坐标为（ ）．A、(1，2) B、（1，0） C、（0，1） D、（2，0）10. 如图，AB∥CD，EG、EM、FM分别平分∠AEF，∠BEF，∠EFD，则图中与∠DFM相等的角（不含它本身）的个数为（ ）
A、5 B、6 C、7 D、8二、填空题
-
11. 点P(m−1，m+3)在平面直角坐标系的y轴上，则P点坐标为.
12. 若是 ，则x=.13. 如图，将一副三角板和一张对边平行的纸条按下列方式摆放，两个三角板的一直角边重合，其中一个三角板的斜边与纸条一边重合，则∠1的度数是.
14. 如图，将一副三角板叠放一起，使直角的顶点重合于点O，则∠AOD +∠COB的度数为度.
15. 如图，一个点在第一，四象限及x轴上运动，在第1次，它从原点运动到点（1，﹣1），用了1秒，然后按图中箭头所示方向运动，即（0，0）→（1，﹣1）→（2，0）→（3，1）→…，它每运动一次需要1秒，那么第2020秒时点所在的位置的坐标是.
三、解答题
-
16. 请完成下面的解答过程完．如图，∠1=∠B，∠C=110°，求∠3的度数．
解：∵∠1=∠B
∴AD∥（ ）（内错角相等，两直线平行）
∴∠C+∠2=180°，（ ）
∵∠C=110°．
∴∠2=（ ）°．
∴∠3=∠2=70°．（ )
17. 计算：(1)、﹣12+ ﹣（﹣2）×(2)、 （ +1）+| ﹣2|18. 已知 的平方根是 ， ，求 的立方根.19. 根据语句画图，并回答问题，如图，∠AOB内有一点P．
(1)、过点P画PC∥OB交OA于点C，画PD∥OA交OB于点D．(2)、写出图中与∠CPD互补的角 ． （写两个即可）(3)、写出图中∠O相等的角 ． （写两个即可）20. 如图，直线 ， 相交于点 ， ，垂足为 .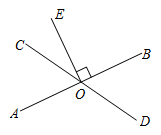
(1)、若 ，求 的度数；(2)、若 ，求 的度数.21. 如图①，将两个边长为1的小正方形分别沿对角线剪开，拼成正方形ABCD．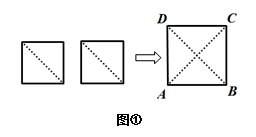
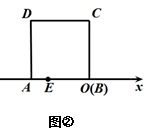(1)、正方形ABCD的面积为 ， 边长为 ， 对角线BD=；(2)、求证： ；(3)、如图②，将正方形ABCD放在数轴上，使点B与原点O重合，边AB落在x轴的负半轴上，则点A所表示的数为 ， 若点E所表示的数为整数，则点E所表示的数为22. 如图，在平面直角坐标系中，点A（0，5），B（﹣2，0），C（3，3），线段AB经过平移得到线段CD，其中点B的对应点为点C，点D在第一象限，直线AC交x轴于点F.
(1)、点D坐标为；(2)、线段CD由线段AB经过怎样平移得到？(3)、求F的坐标.23. 如图1，直线MN与直线AB、CD分别交于点E、F，∠1与∠2互补.
(1)、试判断直线AB与直线CD的位置关系，并说明理由；(2)、如图2，∠BEF与∠EFD的角平分线交于点P，EP与CD交于点G，点H是MN上一点，且GH⊥EG，求证：PF∥GH；(3)、如图3，在（2）的条件下，连接pH，K是GH上一点使∠pHK=∠HPK，作PQ平分∠EPK，求∠HPQ的度数.