河南省信阳市淮滨县2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2021-05-13 类型：期中考试

进入出卷网下载

一、单选题

1. 如图所示的车标，可以看作由“基本图案”经过平移得到的是（）

A、 B、 C、 D、

查看试题解析
2. ∠1与∠2是内错角，∠1=40°，则（）

A、∠2=40° B、∠2=140° C、∠2=40°或∠2=140° D、∠2的大小不确定

查看试题解析
3. 如图， $A B // C D // E F ， A F // C G$ .图中与 $∠ A$ （本身不算）相等的角有（）

A、5个 B、4个 C、3个 D、2个

查看试题解析
4. 下列图形中，线段PQ的长度表示点P到直线L的距离的是（）

A、 B、 C、 D、

查看试题解析
5. 如图，利用直尺和三角尺过直线外一点画已知直线的平行线，这种画法依据的是（）

A、同位角相等，两直线平行 B、两直线平行，同位角相等 C、内错角相等，两直线平行 D、两直线平行，内错角相等

查看试题解析
6. 下列各数： $\frac{22}{7}$ ， $\sqrt[3]{8}$ ， $\frac{π}{2}$ ，﹣1.414， $\sqrt{36}$ ，0.1010010001…中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
7. 下列各数中，可以用来说明命题“任何偶数都是4的倍数”是假命题的反例是（　　）

A、5 B、12 C、14 D、16

查看试题解析
8. 若点M在第四象限，且M到x轴的距离为1，到y轴的距离为2，则点M的坐标为（）

A、（1，﹣2） B、（2，1） C、（﹣2，l） D、（2，﹣l）

查看试题解析
9. 如图，直角三角形ABC的直角边AB=6，BC=8，将直角三角形ABC沿边BC的方向平移到三角形DEF的位置，DE交AC于点G ， BE=2，三角形CEG的面积为13.5，下列结论：①三角形ABC平移的距离是4；②EG=4.5；③AD∥CF；④四边形ADFC的面积为6．其中正确的结论是

A、①② B、②③ C、③④ D、②④

查看试题解析
10. 已知点P到x轴的距离为2，到y轴的距离为3，且点P在x轴的上方，则点P的坐标为（）

A、（2，3） B、（3，2） C、（2，3）或（－2，3） D、（3，2）或（－3，2）

查看试题解析

二、填空题

11. 计算 $\sqrt{64} - \sqrt[3]{64}$ 的结果为.

查看试题解析
12. 如图，AB∥CD，∠B=160°，∠D=120°，则∠E=

查看试题解析
13. 将命题“同角的余角相等”，改写成“如果…，那么…”的形式.

查看试题解析
14. 写出一个大于3且小于4的无理数．

查看试题解析
15. 如图，一把矩形直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE＝125°，则∠DBC的度数为．

查看试题解析
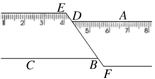16. x﹣2的平方根是±2，2x+y+7的立方根是3，求x²+y²的平方根．

查看试题解析

三、解答题

17. 计算：

(1)、 $| - \sqrt{3} + 2 | + \sqrt{9} - \sqrt[3]{- 8}$ ；

(2)、 $(2 \sqrt{3} + 3 \sqrt{2}) (2 \sqrt{3} - 3 \sqrt{2})$

查看试题解析
18. 如图，AB∥CD，点E是CD上一点，∠AEC＝48°，EF平分∠AED交AB于点F，求∠AFE的度数.

查看试题解析
19. 如图，平面直角坐标系中，△ABC的顶点坐标为：A（1，2），B（2，一1），C（4，3）.

(1)、将△ABC向左平移2个单位长度，再向上平移1个单位长度，得△A＇B＇C＇.画出△A＇B＇C＇，并写出△A＇B＇C＇的顶点坐标；

(2)、求△ABC的面积.

查看试题解析
20. 阅读第（1）题解答过程填理由，并解答第（2）题

(1)、已知：如图 1   AB∥CD，P 为 AB、CD 之间一点，求∠B+∠C+∠BPC 的大小.
解：过点 P 作 PM∥AB

∵AB∥CD（已知）

∴PM∥CD （   ）

∴∠B+∠1=180°（   ）

∴∠C+∠2=180°（   ）

∵∠BPC=∠1+∠2

∴∠B+∠C+∠BPC=360°

(2)、我们生活中经常接触小刀，小刀刀柄外形是一个直角梯形（挖去一个小半圈）如图 2，刀片上、下是平行的，转动刀片时会形成∠1 和∠2，那么∠1+∠2 的大小是否会随刀片的转动面改变？说明理由.

查看试题解析
21. 在平面直角坐标系中，有点A(1，2a+1)，B(﹣a，a﹣3)．

(1)、当点A在第一象限的角平分线上时，求a的值；

(2)、当点B在到x轴的距离是到y轴的距离2倍时，求点B所在的象限位置；

(3)、若线段AB∥x轴，求三角形AOB的面积．

查看试题解析
22. AOCD是放置在平面直角坐标系内的梯形，其中O是坐标原点，点A，C，D的坐标分别为（0，8），（5，0），（3，8）.若点P在梯形内，且 $△ P A D$ 的面积等于 $△ P O C$ 的面积， $△ P A O$ 的面积等于 $△ P C D$ 的面积.
（I）求点P的坐标；

（Ⅱ）试比较∠PAD和∠POC的大小，并说明理由.

查看试题解析
23.

(1)、问题情境
如图1，已知AB∥CD，∠PBA＝125°，∠PCD＝155°，求∠BPC的度数.

佩佩同学的思路：过点P作PG∥AB，进而PG∥CD，由平行线的性质来求∠BPC，求得∠BPC＝

(2)、问题迁移
图2.图3均是由一块三角板和一把直尺拼成的图形，三角板的两直角边与直尺的两边重合，∠ACB＝90°，DF∥CG，AB与FD相交于点E，有一动点P在边BC上运动，连接PE，PA，记∠PED＝∠α，∠PAC＝∠β.

①如图2，当点P在C，D两点之间运动时，请直接写出∠APE与∠α，∠β之间的数量关系；

②如图3，当点P在B，D两点之间运动时，∠APE与∠α，∠β之间有何数量关系？请判断并说明理由；

(3)、拓展延伸
当点P在C，D两点之间运动时，若∠PED，∠PAC的角平分线EN，AN相交于点N，请直接写出∠ANE与∠α，∠β之间的数量关系.

查看试题解析