河南省南阳市唐河县2019-2020学年七年级下学期数学期中考试试卷
试卷更新日期:2021-05-13 类型:期中考试
一、单选题
-
1. 不等式 的解集是( ).A、 B、 C、 D、2. 根据等式的性质,下列变形正确的是( )A、若2x=a,则x=2a B、若 + =1,则3x+2x=1 C、若ab=bc,则a=c D、若 = ,则a=b3. 关于 的一元一次方程 的解为 ,则 的值为( )A、9 B、8 C、5 D、44. 若 ,下列不等式不一定成立的是( )A、 B、 C、 D、5. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、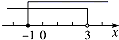 C、
C、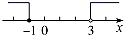 D、
D、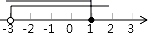 6. 若关于x的不等式组 的解集为x>a,则a的取值范围是( )A、a<2 B、a≤2 C、a>2 D、a≥27. 已知2 2y3a与-4 2ay1+b是同类项,则ba的值为( )A、2 B、-2 C、1 D、-18. 小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少15元.”乙说:“至多12元.”丙说:“至多10元.”小明说:“你们三个人都说错了”.则这本书的价格x(元)所在的范围为( )A、 B、 C、 D、9. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、10. 小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )
6. 若关于x的不等式组 的解集为x>a,则a的取值范围是( )A、a<2 B、a≤2 C、a>2 D、a≥27. 已知2 2y3a与-4 2ay1+b是同类项,则ba的值为( )A、2 B、-2 C、1 D、-18. 小明网购了一本《好玩的数学》,同学们想知道书的价格,小明让他们猜.甲说:“至少15元.”乙说:“至多12元.”丙说:“至多10元.”小明说:“你们三个人都说错了”.则这本书的价格x(元)所在的范围为( )A、 B、 C、 D、9. 《九章算术》中有这样一个题:今有甲乙二人持钱不知其数.甲得乙半而钱五十,乙得甲太半而钱亦五十.问甲、乙持钱各几何?其意思为:今有甲乙二人,不如其钱包里有多少钱,若乙把其一半的钱给甲,则甲的数为50;而甲把其 的钱给乙,则乙的钱数也为50,问甲、乙各有多少钱?设甲的钱数为x,乙的钱数为y,则可建立方程组为( )A、 B、 C、 D、10. 小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图请你根据图中的信息,若小明把100个纸杯整齐叠放在一起时,它的高度约是( )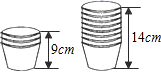 A、106cm B、110cm C、114cm D、116cm
A、106cm B、110cm C、114cm D、116cm二、填空题
-
11. 若 与 互为相反数,则 的值为.12. 下面3个天平左盘中“△”“□”分别表示两种质量不同的物体,则第三个天平右盘中砝码的质量为.
 13. 不等式组 的最大整数解为.14. 在我国明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(倍加增指从塔的顶层到底层).请你算出塔的顶层有盏灯.15. 若关于x的不等式组 恰有两个整数解,则a的取值范围是.
13. 不等式组 的最大整数解为.14. 在我国明代数学家吴敬所著的《九章算术比类大全》中,有一道数学名题叫“宝塔装灯”,内容为“远望巍巍塔七层,红灯点点倍加增;共灯三百八十一,请问顶层几盏灯?”(倍加增指从塔的顶层到底层).请你算出塔的顶层有盏灯.15. 若关于x的不等式组 恰有两个整数解,则a的取值范围是.三、解答题
-
16. 解方程(1)、2(x﹣2)+(4x﹣1)=1.(2)、解下列方程: .(3)、解方程组: .17. 小甘到文具超市去买文具.请你根据如图中的对话信息,求中性笔和笔记本的单价分别是多少元?
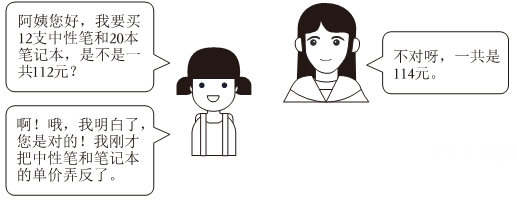 18. 解下列不等式(组),并把它们的解集在数轴上表示出来:(1)、 ;(2)、 .19. 某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.(1)、若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?(2)、若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?20. 已知关于 , 的二元一次方程组 的解满足 ,求满足条件的 的所有非负整数值.21. 某社区购买甲、乙两种树苗进行绿化,已知甲种树苗每棵30元,乙种树苗每棵20元,且乙种树苗棵数比甲种树苗棵数的2倍少40棵,购买两种树苗的总金额为9000元.(1)、求购买甲、乙两种树苗各多少棵?(2)、为保证绿化效果,社区决定再购买甲、乙两种树苗共10棵,总费用不超过230元,求可能的购买方案?22. 先阅读下列解题过程,然后解答后面两个问题.
18. 解下列不等式(组),并把它们的解集在数轴上表示出来:(1)、 ;(2)、 .19. 某校为了开展“阳光体育运动”,计划购买篮球、足球共60个,已知每个篮球的价格为70元,每个足球的价格为80元.(1)、若购买这两类球的总金额为4600元,求篮球、足球各买了多少个?(2)、若购买篮球的总金额不超过购买足球的总金额,求最多可购买多少个篮球?20. 已知关于 , 的二元一次方程组 的解满足 ,求满足条件的 的所有非负整数值.21. 某社区购买甲、乙两种树苗进行绿化,已知甲种树苗每棵30元,乙种树苗每棵20元,且乙种树苗棵数比甲种树苗棵数的2倍少40棵,购买两种树苗的总金额为9000元.(1)、求购买甲、乙两种树苗各多少棵?(2)、为保证绿化效果,社区决定再购买甲、乙两种树苗共10棵,总费用不超过230元,求可能的购买方案?22. 先阅读下列解题过程,然后解答后面两个问题.解方程:|x-3|=2.
解:当x-3≥0时,原方程可化为x-3=2,解得x=5;
当x-3<0时,原方程可化为x-3=-2,解得x=1.
所以原方程的解是x=5或x=1.
(1)、解方程:|3x-2|-4=0.(2)、解关于x的方程:|x-2|=b+123. 每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)、求甲、乙两种型号设备的价格;(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;(3)、在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.