河南省南阳市方城县2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2021-05-13 类型：期中考试

进入出卷网下载

一、单选题

1. 下面四个等式的变形中正确的是（）

A、由 $4 x + 8 = 0$ 得 $x + 2 = 0$ B、由 $x + 7 = 5 - 3 x$ 得 $4 x = 2$ C、由 $\frac{3}{5} x = 4$ 得 $x = \frac{12}{5}$ D、由 $- 4 (x - 1) = - 2$ 得 $4 x = - 6$

查看试题解析
2. 下列方程：① $2 x - \frac{y}{3} = 1$ ；② $\frac{x}{2} + \frac{3}{y} = 3$ ；③ $x^{2} - y^{2} = 4$ ；④ $5 (x + y) = 7 (x - y)$ ；⑤ $2 x^{2} = 3$ ；⑥ $x + \frac{1}{y} = 4$ ，其中是二元一次方程的是（）

A、① B、①④ C、①③ D、①②④⑥

查看试题解析
3. 语句“x的 $\frac{1}{8}$ 与x的和不超过5”可以表示为（）

A、 $\frac{x}{8}$ +x≤5 B、 $\frac{x}{8}$ +x≥5 C、 $\frac{8}{x + 5}$ ≤5 D、 $\frac{x}{8}$ +x＝5

查看试题解析
4. 已知 ${\begin{array}{l} x = 3 \\ y = - 2 \end{array}$ 是二元一次方程3x﹣my＝5的一组解，则m的值为（）

A、﹣2 B、2 C、﹣ $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
5. 不等式组 ${\begin{matrix} x + 5 > 3 \\ x + 6 > 4 x - 3 \end{matrix}$ 的整数解的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
6. 小明在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程是：，怎么呢？小明想了一想，便翻看书后答案，此方程的解是 $y = - \frac{5}{3}$ ，很快补好了这个常数，并迅速地完成了作业，同学们，你们能补出这个常数吗？它应是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 若方程组 ${\begin{array}{l} 2 x + y = 1 - 3 k \\ x + 2 y = 2 \end{array}$ 的解满足 $x + y > 1,$ 则 $k$ 的取值范围是（）

A、 $k > 2$ B、 $k < 2$ C、 $k > 0$ D、 $k < 0$

查看试题解析
8. 把1400元的奖金按两种奖给22名学生，其中一等奖每人200元，二等奖每人50元，设获一等奖的学生有x人，则下列方程错误的是（）

A、 $(200 - 50) x + 50 \times 22 = 1400$ B、 $\frac{1400 - 200 x}{50} + x = 22$ C、 $50 x + 200 (22 - x) = 1400$ D、 $200 x + 50 (22 - x) = 1400$

查看试题解析
9. 已知 $x = m + 15$ ， $y = 5 - 2 m$ ，若 $m > - 3$ ，则x与y的关系为（）

A、 $x = y$ B、 $x > y$ C、 $x < y$ D、不能确定

查看试题解析
10. 如图，在长为15，宽为12的矩形中，有形状、大小完全相同的5个小矩形，则图中阴影部分的面积为（）

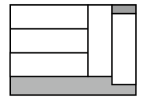A、35 B、45 C、55 D、65

查看试题解析

二、填空题

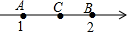
11. 方程3x+1=7的根是．

查看试题解析
12. 已知 $| 2 x - 4 | + | x + 2 y - 8 | = 0$ ，则 ${(x - y)}^{2020} =$ .

查看试题解析
13. 如图所示，点C位于点A、B之间（不与A、B重合），点C表示 $1 ﹣ 2 x$ ，则x的取值范围是．

查看试题解析
14. 如图，在实数范围内规定新运算“△”，其规则是：a△b=2a﹣b．已知不等式x△k≥1的解集在数轴上，则k的值是．

查看试题解析

15. 在“元旦”期间，平价商场对该商场商品进行如下的优惠促销活动：

打折前一次性购物总金额	优惠措施
小于等于 400 元	不优惠
超过 400 元，但不超过 600元	按售价打九折
超过 600 元	其中 600 元部分八折优惠，超过 600 元的部分打六折优惠

按上述优惠条件，若小华一次性购买售价为 80 元/件的商品 n 件时，实际付款 504 元，则 n=.

查看试题解析

三、解答题

16.

(1)、 $\frac{2}{5} x - 8 = \frac{1}{4} - 0.2 x$

(2)、 $\frac{3 x - 1}{2} = \frac{4 x + 2}{5} - 1$

查看试题解析
17. 阅读小强同学数学作业本上的截图内容并完成任务：
解方程组 ${\begin{array}{l} 2 x - y = 3 ① \\ x + y = - 12 ② \end{array}$

解：由①，得 $y = 2 x - 3$ ，③ 第一步

把③代入①，得 $2 x - (2 x - 3) = 3$ .第二步

整理得， $3 = 3$ .第三步

因为 $x$ 可以取任意实数，所以原方程组有无数个解第四步

任务：

(1)、这种解方程组的方法称为；

(2)、利用此方法解方程组的过程中所体现的数学思想是_______；（请你填写正确选项）

A、转化思想 B、函数思想 C、数形结合思想 D、公理化思想

(3)、小强的解法正确吗？（填正确或不正确），如果不正确，请指出错在第步，请选择恰当的解方程组的方法解该方程组.

查看试题解析
18.

(1)、当 $x$ 取何值时，代数式 $\frac{x + 4}{3}$ 与 $\frac{3 x - 1}{2}$ 的值的差大于 $1$ ？

(2)、解不等组： ${\begin{array}{l} 5 x + 4 < 3 (x + 1) \\ \frac{x - 1}{2} \geq \frac{2 x - 1}{5} \end{array}$ （注意：用数轴确定不等式组的解集）

查看试题解析
19. 小明解方程 $\frac{2 x - 6}{5} + 1 = \frac{x + a}{2}$ 时，由于粗心大意，在去分母时，方程左边的 $1$ 没有乘以 $10$ ，由此得到方程的解为 $x = - 1$ ，试求 $a$ 的值，并正确地求出原方程的解.

查看试题解析
20. 已知，关于x，y的方程组 ${\begin{array}{l} x - y = 4 a - 3 \\ x + 2 y = - 5 a \end{array}$ 的解为x、y.

(1)、x＝， y＝（用含a的代数式表示）；

(2)、若x、y互为相反数，求a的值；

查看试题解析
21. 某中学七年级同学要在清明节到烈士陵园扫墓，计划制作 $418$ 朵小白花学生会主席小琳先做了 $2$ 天，后来好朋友小雯也加入一起做了 $3$ 天，最后比计划多制作 $32$ 朵小白花.已知小雯每天比小琳少制作 $2$ 朵小白花.请问：小琳、小雯平均每天分别能制作多少朵小白花？

查看试题解析
22. 阅读下列材料，然后解答后面的问题.
我们知道方程2x+3y=12有无数组解，但在实际生活中我们往往只需要求出其正整数解.例：由2x+3y=12，得 $y = \frac{12 - 2 x}{3} = 4 - \frac{2}{3} x$ ，（x、y为正整数）∴ $\{\begin{cases} x ＞ 0 \\ \frac{12 - x}{3} ＞ 0 \end{cases}$ 则有0＜x＜6.又 $y = 4 - \frac{2}{3} x$ 为正整数，则 $\frac{2}{3} x$ 为正整数.

由2与3互质，可知：x为3的倍数，从而x=3，代入 $y = 4 - \frac{2}{3} x = 2$ .

∴2x+3y=12的正整数解为 $\{\begin{cases} x = 3 \\ y = 2 \end{cases}$

问题：

(1)、请你写出方程2x+y=5的一组正整数解：；

(2)、若 $\frac{6}{x - 2}$ 为自然数，则满足条件的x值有______个；

A、2 B、3 C、4 D、5

(3)、七年级某班为了奖励学习进步的学生，购买了单价为3元的笔记本与单价为5元的钢笔两种奖品，共花费35元，问有几种购买方案？

查看试题解析
23. 学校“百变魔方”社团准备购买 $A ， B$ 两种魔方.已知购买 $2$ 个 $A$ 种魔方和 $6$ 个 $B$ 种魔方共需 $130$ 元；购买 $3$ 个 $A$ 种魔方所需款数和购买 $4$ 个 $B$ 种魔方所需款数相同.优惠活动：活动一：“疯狂打折”： $A$ 种魔方八折， $B$ 种魔方四折；活动二：“买一送一”：购买一个 $A$ 种魔方送一个 $B$ 种魔方

(1)、求 $A 、 B$ 这两种魔方的单价；

(2)、结合社员们的需求，社团决定购买 $A 、 B$ 两种魔方共 $100$ 个（其中 $A$ 种魔方不超过 $50$ 个） .某商店有两种优惠活动，如图所示.设购买 $A$ 种魔方 $m$ 个，按活动一购买所需费用为 $w_{1}$ 元，按活动二购买所需费用为 $w_{2}$ 元.请根据以上信息，解决以下问题：
①试用含 $m$ 的代数式分别表示 $w_{1} 、 w_{2}$ .

②试求当购买 $A$ 种魔方多少个时，选择两种优惠活动同样实惠？

③以 $A$ 种魔方的个数说明选择哪种优惠活动购买魔方更实惠.

查看试题解析