河南省洛阳市汝阳县2019-2020学年七年级下学期数学期中考试试卷

试卷更新日期：2021-05-13 类型：期中考试

进入出卷网下载

一、单选题

1. 下面四个等式的变形中正确的是（）

A、由2x+4＝0得x+2＝0 B、由x+7＝5﹣3x得4x＝2 C、由 $\frac{3}{5}$ x＝4得x＝ $\frac{12}{5}$ D、由﹣4（x﹣1）＝﹣2得4x＝﹣6

查看试题解析
2. 用代入消元法解方程组 ${\begin{array}{l} 3 x + 4 y = 2 ① \\ 2 x - y = 5 ② \end{array}$ 使得代入后化简比较容易的变形是（）

A、由①得 $x = \frac{2 - 4 y}{3}$ B、由①得 $y = \frac{2 - 3 x}{4}$ C、由②得 $x = \frac{y + 5}{2}$ D、由②得y＝2x－5

查看试题解析
3. 以 ${\begin{cases} x = 3 \\ y = 1 \\ z = - 1 \end{cases}$ 为解建立三元一次方程组，不正确的是（）

A、 $3 x - 4 y + 2 z = 3$ B、 $\frac{1}{3} x - y + z = - 1$ C、 $x + y - z = - 2$ D、 $\frac{x}{2} - \frac{2}{3} y - z = 1 \frac{5}{6}$

查看试题解析
4. 若m，n满足|2m+1|+（n﹣2）²＝0，则mn的值等于（）

A、1 B、﹣1 C、﹣2 D、2

查看试题解析
5. 在方程组 ${\begin{array}{l} 2 x + y = 1 - m \\ x + 2 y = 2 \end{array}$ 中，若未知数x，y满足x+y＞0，则m的取值范围在数轴上的表示应是如图所示的（）

A、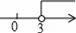 B、 C、 D、

查看试题解析
6. 某车间有26名工人，每人每天可以生产800个螺钉或1000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套．设安排x名工人生产螺钉，则下面所列方程正确的是（　　）

A、2×1000（26﹣x）=800x B、1000（13﹣x）=800x C、1000（26﹣x）=2×800x D、1000（26﹣x）=800x

查看试题解析
7. 为了鼓励市民节约用电，某市对居民用电实行“阶梯收费”（总电费＝第一阶梯电费+第二阶梯电费）.规定：用电量不超过200度按第一阶梯电价收费，超过200度的部分按第二阶梯电价收费.如图是张磊家2015年9月和10月所交电费的收据，则该市规定的第一阶梯电价和第二阶梯电价分别为每度（）

A、0.5元、0.6元 B、0.4元、0.5元 C、0.3元、0.4元 D、0.6元、0.7元

查看试题解析
8. 小方、小红和小军三人玩飞镖游戏，各投四支飞镖，规定在同一圆环内得分相同，中靶和得分情况如图，则小红的得分是（）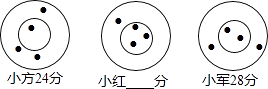

A、30分 B、32分 C、33分 D、34分

查看试题解析
9. 现规定一种运算： $a * b = a b + a - b$ ，其中 $a ， b$ 为常数，若 $2 * 3 + m * 1 = 6$ ，则不等式 $\frac{3 x + 2}{2} < m$ 的解集是（）

A、 $x < - 2$ B、 $x < - 1$ C、 $x < 0$ D、 $x > 2$

查看试题解析
10. 若不等式组 ${\begin{array}{l} x + a \geq 0 \\ 4 - 2 x > x - 2 \end{array}$ 有解，则实数 $a$ 的取值范围是（）.

A、 $a \geq - 2$ B、 $a < - 2$ C、 $a \leq - 2$ D、 $a > - 2$

查看试题解析

二、填空题

11. 方程x﹣3＝0的解是.

查看试题解析
12. 请用不等式表示“x的2倍与3的和不大于1”：．

查看试题解析
13. 如图1，在边长为a的大正方形中剪去一个边长为b的小正方形，再将图中的阴影部分剪拼成一个长方形，如图2.这个拼成的长方形的长为30，宽为20.则图2中Ⅱ部分的面积是
.

查看试题解析
14. 小亮解方程组 ${\begin{matrix} 2 x + y = ● \\ 2 x - y = 12 \end{matrix}$ 的解为 ${\begin{matrix} x = 5 \\ y = ★ \end{matrix}$ ，由于不小心，滴上了两滴墨水，刚好遮住了两个数 $●$ 和★，请你帮他找回 $★$ 这个数， $★$ = ．

查看试题解析
15.
对一个实数x按如图所示的程序进行操作，规定：程序运行从“输入一个实数x”到“结果是否大于88？”为一次操作．如果操作只进行一次就停止，则x的取值范围是．

查看试题解析

三、解答题

16. 解方程组 ${\begin{array}{l} 3 x = 8 - y \\ 3 x + 5 y = 16 \end{array}$ .

查看试题解析
17. 定义新运算为：对应任意实数a、b都有 $a \oplus b = （ a-b ） b- 1 ，$ 等式右边都是通常的加法、减法、乘法运算，比如 $1 \oplus 2$ =（1-2）×2-1=-3.

(1)、（-3） $\oplus$ 4的值为；

(2)、若x $\oplus$ 2的值小于5，求x的取值范围，并在如图所示的数轴上表示出来.

查看试题解析
18. 已知关于 $x$ ， $y$ 的方程组 ${\begin{array}{l} x - 2 y = m, \\ 2 x + 3 y = 2 m + 4 \end{array}$ 的解满足不等式组 ${\begin{array}{l} 3 x + y \leq 0 \\ x + 5 y > 0 \end{array}$ ，求满足条件的 $m$ 的整数值．

查看试题解析
19. 某天张新和李明相约到图书城买书，请你根据他们的对话内容（如图），求出李明上次购买书籍的原价.

查看试题解析
20. 我们规定，若关于x的一元一次方程ax＝b的解为b﹣a，则称该方程为“差解方程”，例如：2x＝4的解为2，且2＝4﹣2，则该方程2x＝4是差解方程.

(1)、判断3x＝4.5是否是差解方程；

(2)、若关于x的一元一次方程5x＝m+1是差解方程，求m的值.

查看试题解析
21. 阅读以下内容：
已知实数x，y满足x＋y＝2，且 ${\begin{array}{l} 3 x + 2 y = 7 k - 2 \\ 2 x + 3 y = 6 \end{array}$ ，k的值.

三名同学分别提出了以下三种不同的解题思路：

甲同学：先解关于x，y的方程组 ${\begin{array}{l} 3 x + 2 y = 7 k - 2 \\ 2 x + 3 y = 6 \end{array}$ ，求k的值.

乙同学：先将方程组中的两个方程相加，再求k的值.

丙同学：先解方程组 ${\begin{array}{l} x + y = 2 \\ 2 x + 3 y = 6 \end{array}$ ，再求k的值.

你最欣赏以上哪名同学的解题思路？先根据你所选的思路解答此题，再对你选择的思路进行简要评价.

（评价参考建议：基于观察到题目的什么特征设计的相应思路，如何操作才能实现这些思路、运算的简洁性，以及你依此可以总结出什么解题策略等）

查看试题解析
22. 某商贸公司有 $A$ 、 $B$ 两种型号的商品需运出，这两种商品的体积和质量分别如下表所示：

体积（立方米/件）

质量（吨/件）

$A$ 型商品

0.8

0.5

$B$ 型商品

2

1

(1)、已知一批商品有 $A$ 、 $B$ 两种型号，体积一共是20立方米，质量一共是10.5吨，求 $A$ 、 $B$ 两种型号商品各有几件？

(2)、物资公司现有可供使用的货车每辆额定载重3.5吨，容积为6立方米，其收费方式有以下两种：
①按车收费：每辆车运输货物到目的地收费600元；

②按吨收费：每吨货物运输到目的地收费200元.

现要将（1）中商品一次或分批运输到目的地，如果两种收费方式可混合使用，商贸公司应如何选择运送、付费方式，使其所花运费最少，最少运费是多少元？

查看试题解析
23. 某中学开学初到商场购买A、B两种品牌的足球，购买A种品牌的足球50个，B种品牌的足球25个，共花费4500元，已知购买一个B种品牌的足球比购买一个A种品牌的足球多花30元．

(1)、求购买一个A种品牌、一个B种品牌的足球各需多少元．

(2)、学校为了响应习总书记“足球进校园”的号召，决定再次购进A、B两种品牌足球共50个，正好赶上商场对商品价格进行调整，A品牌足球售价比第一次购买时提高4元，B品牌足球按第一次购买时售价的9折出售，如果学校此次购买A、B两种品牌足球的总费用不超过第一次花费的70%，且保证这次购买的B种品牌足球不少于23个，则这次学校有哪几种购买方案？

(3)、请你求出学校在第二次购买活动中最多需要多少资金？

查看试题解析

	体积（立方米/件）	质量（吨/件）
$A$ 型商品	0.8	0.5
$B$ 型商品	2	1