江苏省扬州市江都区2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-05-13 类型:期末考试
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 早在两千多年前,中国人已经开始使用负数,并应用到生产和生活中.中国人使用负数在世界上是首创.下列各式计算结果为负数的是( )A、 B、 C、 D、3. 若方程 的解是 ,则a的值为( )A、 B、 C、 D、4. 某几何体的展开图如图所示,该几何体是( )
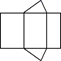 A、三棱柱 B、圆锥 C、四棱柱 D、圆柱5. 2020年3月14日,是人类第一个“国际数学日”.这个节日的昵称是“ ”.在古代,一个国家所算得的圆周率的精确程度,可以作为衡量这个国家当时数学与科技发展水平的一个主要标志.我国南北朝时的祖冲之是世界上最早把圆周率的精确值计算到小数点后第7位的科学巨匠,该成果领先世界一千多年.以下对于圆周率的四个表述:
A、三棱柱 B、圆锥 C、四棱柱 D、圆柱5. 2020年3月14日,是人类第一个“国际数学日”.这个节日的昵称是“ ”.在古代,一个国家所算得的圆周率的精确程度,可以作为衡量这个国家当时数学与科技发展水平的一个主要标志.我国南北朝时的祖冲之是世界上最早把圆周率的精确值计算到小数点后第7位的科学巨匠,该成果领先世界一千多年.以下对于圆周率的四个表述:①圆周率是一个有理数; ②圆周率是一个无理数;
③圆周率是一个与圆的大小有关的常数; ④圆周率是一个与圆的大小无关的常数.
其中表述正确的序号是( )
A、 ①③ B、①④ C、②③ D、②④6. 如图,已知线段AB=12cm,点N在AB上,NB=2cm,M是AB中点,那么线段MN 的长为 ( )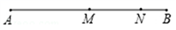 A、5cm B、4 C、3 D、27. 把根绳子对折成一条线段 ,在线段 取一点 ,使 ,从 处把绳子剪断,若剪断后的三段绳子中最长的一段为 ,则绳子的原长为( )A、 B、 C、 或 D、 或8. 若 个数 、 、…、 满足下列条件: , , ,…, ,则 的值为( )A、 B、 C、 D、
A、5cm B、4 C、3 D、27. 把根绳子对折成一条线段 ,在线段 取一点 ,使 ,从 处把绳子剪断,若剪断后的三段绳子中最长的一段为 ,则绳子的原长为( )A、 B、 C、 或 D、 或8. 若 个数 、 、…、 满足下列条件: , , ,…, ,则 的值为( )A、 B、 C、 D、二、填空题
-
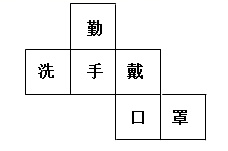
9. 若 , 是同类项,则 .10. 一个直角三角形绕它的一条直角边旋转一周得到的几何体是.11. 某正方体的每个面上都有一个汉字,如图是它的一种表面展开图,那么在原正方本中,与“勤”字所在面相对面上的汉字是.
 12. 若 ,则 .13. 实数 在数轴上的位置上如图所示,则化简 的结果为 .
12. 若 ,则 .13. 实数 在数轴上的位置上如图所示,则化简 的结果为 . 14. 已知 ,则 的补角等于 .15. 把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本,这个班的学生有人.16. 时钟上 点 分时,时针与分针的夹角为.17. 如图①, 为直线 上一点,作射线 ,使 ,将一个直角三角尺如图摆放,直角顶点在点 处,一条直角边 在射线 上,将图①中的三角尺绕点 以每秒 的速度按顺时针方向旋转(如图②所示),在旋转一周的过程中第 秒时 所在直线恰好平分 ,则 的值为.
14. 已知 ,则 的补角等于 .15. 把一些图书分给某班学生阅读,如果每人分3本,则剩余20本;如果每人分4本,则还缺25本,这个班的学生有人.16. 时钟上 点 分时,时针与分针的夹角为.17. 如图①, 为直线 上一点,作射线 ,使 ,将一个直角三角尺如图摆放,直角顶点在点 处,一条直角边 在射线 上,将图①中的三角尺绕点 以每秒 的速度按顺时针方向旋转(如图②所示),在旋转一周的过程中第 秒时 所在直线恰好平分 ,则 的值为.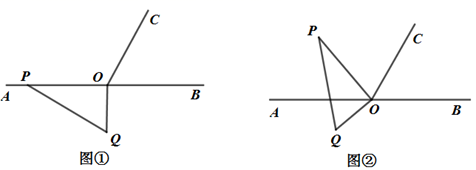
三、解答题
-
18. 计算:(1)、(2)、19. 解下列方程:(1)、 ;(2)、 .20. 先化简,再求值: ,其中 , .21. 如图所示的方格纸中,每个小正方形的边长为 ,每个小正方形的顶点叫格点,请利用格点画图.
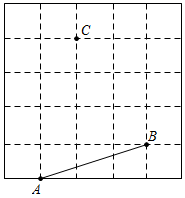 (1)、过点 画 的平行线,并标出经过的格点 ;过点 画 的垂线,垂足为 ,并标出经过的格点 ;(2)、直线 与直线 的位置关系.(3)、三角形 的面积是.22. 一艘船从甲码头到乙码头顺流行驶,用了 小时;从乙码头返回甲码头逆流行驶,用了 小时.已知水流的速度是 千米/时,求船在静水中的平均速度.23. 如图,线段AB=8,点C是线段AB的中点,点D是线段BC的中点.
(1)、过点 画 的平行线,并标出经过的格点 ;过点 画 的垂线,垂足为 ,并标出经过的格点 ;(2)、直线 与直线 的位置关系.(3)、三角形 的面积是.22. 一艘船从甲码头到乙码头顺流行驶,用了 小时;从乙码头返回甲码头逆流行驶,用了 小时.已知水流的速度是 千米/时,求船在静水中的平均速度.23. 如图,线段AB=8,点C是线段AB的中点,点D是线段BC的中点.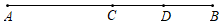 (1)、求线段AD的长;(2)、若在线段AB上有一点E , CE= BC , 求AE的长.24. 如图是由 个棱长为 的小正方体搭成的几何体.
(1)、求线段AD的长;(2)、若在线段AB上有一点E , CE= BC , 求AE的长.24. 如图是由 个棱长为 的小正方体搭成的几何体. (1)、请分别面出这个几何体的主视图、左视图和俯视图;
(1)、请分别面出这个几何体的主视图、左视图和俯视图; (2)、这个几何体的表面积为(包括底面积);(3)、用小正方体搭一几何体,使得它的俯视图和左视图与你在(1)中所画的图形一致,则搭这样的几何体最少要个小正方体.25. 如图,直线 与 相交于点 , .
(2)、这个几何体的表面积为(包括底面积);(3)、用小正方体搭一几何体,使得它的俯视图和左视图与你在(1)中所画的图形一致,则搭这样的几何体最少要个小正方体.25. 如图,直线 与 相交于点 , . (1)、如果 ,那么根据 , 可得 .(2)、如果 ,求 的度数.26. 如图,已知 、 是数轴上的两个点,点 表示的数为 ,点 表示的数为 ,动点 从点 出发,以每秒 个单位长度的速度沿数轴向右匀速运动,设运动时间为 秒.
(1)、如果 ,那么根据 , 可得 .(2)、如果 ,求 的度数.26. 如图,已知 、 是数轴上的两个点,点 表示的数为 ,点 表示的数为 ,动点 从点 出发,以每秒 个单位长度的速度沿数轴向右匀速运动,设运动时间为 秒. (1)、 , 点 表示的数(分别用含 的代数式表示);(2)、点 运动多少秒时, ?(3)、若 为 的中点, 为 的中点,点 在运动的过程中,线段 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段 的长.27. (阅读理解)
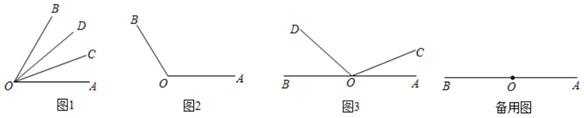
(1)、 , 点 表示的数(分别用含 的代数式表示);(2)、点 运动多少秒时, ?(3)、若 为 的中点, 为 的中点,点 在运动的过程中,线段 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段 的长.27. (阅读理解)射线 是 内部的一条射线,若 ,则我们称射线 是射线 的伴随线.如图1, , ,则 ,称射线 是射线 的伴随线;同时,由于 ,称射线 是射线 的伴随线.
 (1)、(知识运用)
(1)、(知识运用)如图2, ,射线 是射线 的伴随线,则 .若 的度数是 ,射线 是射线 的伴随线,则 的度数是.(用含 的代数式表示).
(2)、如图 , ,射线 与射线 重合,并绕点 以每秒 的速度逆时针旋转,射线 与射线 重合,并绕点 以每秒 的速度顺时针旋转,当射线 与射线 重合时,运动停止.①是否存在某个时刻 (秒),使得 的度数是 ,若存在,求出 的值,若不存在,请说明理由.
②当 为多少秒时,射线 、 、 中恰好有一条射线是其余两条射线中某一条射线的伴随线,请直接写出 的值.