江苏省宿迁市沭阳县2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-05-13 类型:期末考试
一、单选题
-
1. 数1,0, ,﹣2中最大的是( )A、1 B、0 C、 D、﹣22. 如图所示的几何体的左视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、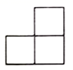 3. 下列运算中,结果正确的是( )A、 B、 C、 D、4. 下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )A、
3. 下列运算中,结果正确的是( )A、 B、 C、 D、4. 下列正方体的展开图上每个面上都有一个汉字.其中,手的对面是口的是( )A、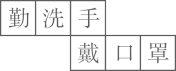 B、
B、 C、
C、 D、
D、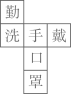 5. 下列说法错误的是( )A、平面内过一点有且只有一条直线与已知直线平行 B、平面内过一点有且只有一条直线与已知直线垂直 C、两点之间的所有连线中,线段最短 D、对顶角相等6. 如图,数轴的单位长度为1,如果点 表示的数为-2,那么点 表示的数是( ).
5. 下列说法错误的是( )A、平面内过一点有且只有一条直线与已知直线平行 B、平面内过一点有且只有一条直线与已知直线垂直 C、两点之间的所有连线中,线段最短 D、对顶角相等6. 如图,数轴的单位长度为1,如果点 表示的数为-2,那么点 表示的数是( ). A、-1 B、0 C、3 D、47. 如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x,则列出方程正确的是( )
A、-1 B、0 C、3 D、47. 如图,在编写数学谜题时,“□”内要求填写同一个数字,若设“□”内数字为x,则列出方程正确的是( ) A、 B、 C、 D、8. 如图,把一根绳子对折成线段AB,从点P处把绳子剪断,已知 ,若剪断后的各段绳子中最长的一段为40cm,则绳子的原长为( )
A、 B、 C、 D、8. 如图,把一根绳子对折成线段AB,从点P处把绳子剪断,已知 ,若剪断后的各段绳子中最长的一段为40cm,则绳子的原长为( ) A、30cm B、60cm C、120cm D、60cm或120cm
A、30cm B、60cm C、120cm D、60cm或120cm二、填空题
-
9. 一元一次方程 的解是 .10. 已知 ,则 的补角是°'.11. 写出一个无理数,使这个无理数的绝对值小于4:.12. 我国自主研发的“北斗系统”现已广泛应用于国防、生产和生活等各个领域,多项技术处于国际领先地位,其星载原子钟的精度,已经提升到了每3000000年误差1秒,数3000000用科学记数法表示为.13. 如图为一个长方体,则该几何体主视图的面积为cm2.
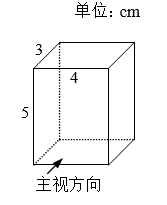 14. 如图,直线 , 相交于点 , ,垂足为点 ,若 ,则 的度数为.
14. 如图,直线 , 相交于点 , ,垂足为点 ,若 ,则 的度数为.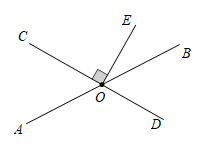 15. 如果 ,那么代数式 的值为.16. 关于x的方程2x+5a=3的解与方程2x+2=0的解相同,则a的值是 .17. 暑假期间,亮视眼镜店开展学生配镜优惠活动,某款式眼镜的广告如图,请你为广告牌填上原价.原价:元
15. 如果 ,那么代数式 的值为.16. 关于x的方程2x+5a=3的解与方程2x+2=0的解相同,则a的值是 .17. 暑假期间,亮视眼镜店开展学生配镜优惠活动,某款式眼镜的广告如图,请你为广告牌填上原价.原价:元 18. 在同一平面内,∠BOC=50°,OA⊥OB,OD平分∠AOC,则∠BOD的度数是.
18. 在同一平面内,∠BOC=50°,OA⊥OB,OD平分∠AOC,则∠BOD的度数是.三、解答题
-
19.(1)、计算:(2)、先化简,再求值: ,其中 .20. 解方程(1)、 ;(2)、21. 已知,点C是线段AB的中点, .点D在线段CB上,且 ,求线段CD的长.
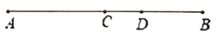 22. 如图,直线AC、BD相交于点O,OE是 的平分线, ,试求 的度数.
22. 如图,直线AC、BD相交于点O,OE是 的平分线, ,试求 的度数.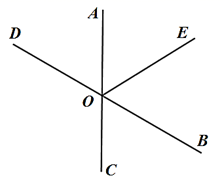 23. 根据要求完成画图或作答:
23. 根据要求完成画图或作答:如图所示,已知点 、 、 是网格纸上的三个格点.
 (1)、画射线 ,画线段 ,过点 画 的平行线 ;(2)、过点 画直线 的垂线,垂足为点 ,则点 到 的距离就是线段的长度.(3)、线段 线段 (填“ ”或“ ”),理由是.24. 课外活动中一些学生分组参加活动,原来每组6人,后来重新编组,每组8人,这样就比原来减少2组,问这些学生共有多少人?25. 按要求完成下列视图问题, 其中小正方体的棱长为
(1)、画射线 ,画线段 ,过点 画 的平行线 ;(2)、过点 画直线 的垂线,垂足为点 ,则点 到 的距离就是线段的长度.(3)、线段 线段 (填“ ”或“ ”),理由是.24. 课外活动中一些学生分组参加活动,原来每组6人,后来重新编组,每组8人,这样就比原来减少2组,问这些学生共有多少人?25. 按要求完成下列视图问题, 其中小正方体的棱长为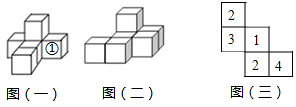 (1)、如图 一 ,它是由六个同样大小的正方体摆成的几何体 将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(1)、如图 一 ,它是由六个同样大小的正方体摆成的几何体 将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?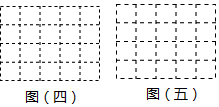 (2)、如图 二 ,请你借助虚线网格 图四 画出该几何体的俯视图,该几何体的体积为.(3)、如图 三 ,它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助虚线网格 图五 画出该几何体的主视图.26. 规定一种新运算法则: ,例如(1)、求 的值;(2)、若 ,求 的值.27. 自来水公司为限制开发区单位用水,规定某单位每月计划内用水300吨,计划内用水每吨收费3元,超计划部分每吨按4元收费.(1)、某月该单位用水260吨,水费是元;若用水350吨,则水费是元.(2)、设该单位每月用水量为 吨,填表(用含 的代数式表示):
(2)、如图 二 ,请你借助虚线网格 图四 画出该几何体的俯视图,该几何体的体积为.(3)、如图 三 ,它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助虚线网格 图五 画出该几何体的主视图.26. 规定一种新运算法则: ,例如(1)、求 的值;(2)、若 ,求 的值.27. 自来水公司为限制开发区单位用水,规定某单位每月计划内用水300吨,计划内用水每吨收费3元,超计划部分每吨按4元收费.(1)、某月该单位用水260吨,水费是元;若用水350吨,则水费是元.(2)、设该单位每月用水量为 吨,填表(用含 的代数式表示):用水量 (吨)
小于等于300吨
大于300吨
水费(元)
(3)、若某月该单位缴纳水费1300元,则该单位这个月用水多少吨?28. 如图,在数轴上点A表示的数是-4;点B在点A的右侧,且到点A的距离是24;点C在点A与点B之间,且 .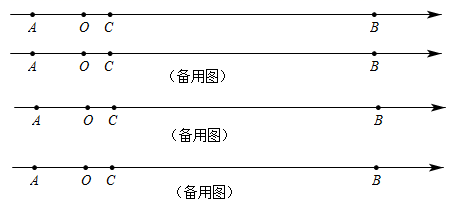 (1)、点B表示的数是 , 点C表示的数是;(2)、若点P从点A出发,沿数轴以每秒3个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒,在运动过程中,
(1)、点B表示的数是 , 点C表示的数是;(2)、若点P从点A出发,沿数轴以每秒3个单位长度的速度向右匀速运动;同时,点Q从点B出发,沿数轴以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒,在运动过程中,①当t为何值时,点P与点Q相遇?
②当t为何值时,点P与点Q间的距离为9个单位长度?
(3)、在(2)的条件下,在运动过程中,是否存在某一时刻使得 ?若存在,请求出此时点P表示的数;若不存在,请说明理由.