江苏省南通市如皋市2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-05-13 类型:期末考试
一、单选题
-
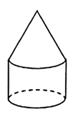
1. 的相反数是( )A、 B、 C、5 D、2. 苏中国际集装箱码头位于国家一类开放口岸——如皋港,2020年该码头集装箱吞吐量目标突破500000箱,致力打造长江下游集装箱港口“小巨人”.请将数500000用科学记数法表示为( )A、 B、 C、500000 D、3. 将下列平面图形绕轴旋转一周,能得到图中所示立体图形的是( )
 A、
A、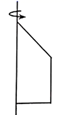 B、
B、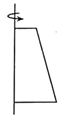 C、
C、 D、
D、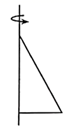 4. 如果 是关于 的方程 的解,则 的值是( )A、 B、 C、 D、5. 下列各式中,与3x2y3是同类项的是( )
4. 如果 是关于 的方程 的解,则 的值是( )A、 B、 C、 D、5. 下列各式中,与3x2y3是同类项的是( )
A、 B、 C、 D、6. 如图, ,以 为一边作 ,则 的度数为( )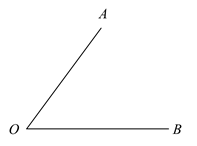 A、 B、 C、 或 D、 或7. 已知九年级某班30位同学种树72棵,男生每人种3棵,女生每人种2棵,设男生x人,则 ( )A、 B、 C、 D、8. 延长线段 到 ,使 ,若 ,点 为线段 的中点,则 的长为( )A、2 B、4 C、6 D、89. 在有理数范围内定义运算“ ”: ,如: .如果 成立,则 的值是( )A、 B、5 C、0 D、210. 已知 都是不等于0的有理数,若 ,则 等于1或 ;若 ,则 等于2或 或0;若 ,则 所有可能等于的值的绝对值之和等于( )A、0 B、110 C、210 D、220
A、 B、 C、 或 D、 或7. 已知九年级某班30位同学种树72棵,男生每人种3棵,女生每人种2棵,设男生x人,则 ( )A、 B、 C、 D、8. 延长线段 到 ,使 ,若 ,点 为线段 的中点,则 的长为( )A、2 B、4 C、6 D、89. 在有理数范围内定义运算“ ”: ,如: .如果 成立,则 的值是( )A、 B、5 C、0 D、210. 已知 都是不等于0的有理数,若 ,则 等于1或 ;若 ,则 等于2或 或0;若 ,则 所有可能等于的值的绝对值之和等于( )A、0 B、110 C、210 D、220二、填空题
-
11. 计算: .12. 已知 ,那么 的补角等于.13. 某正方体每个面上都有一个汉字,如图是它的一种展开图,那么在原正方体中,与“爱”字所在面相对的面上的汉字是.
 14. 古代名著《算学启蒙》中有一题:“良马日行二百四十里.驽马日行一百五十里.驽马先行一十二日,问良马几何追及之.”意思是:“跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马天可追上慢马.”15. 已知关于 的多项式 与多项式 的和不含 项,则 的值为.16. 如图, 平分 , ,则 .
14. 古代名著《算学启蒙》中有一题:“良马日行二百四十里.驽马日行一百五十里.驽马先行一十二日,问良马几何追及之.”意思是:“跑得快的马每天走240里,跑得慢的马每天走150里.慢马先走12天,快马天可追上慢马.”15. 已知关于 的多项式 与多项式 的和不含 项,则 的值为.16. 如图, 平分 , ,则 .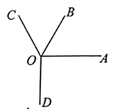 17. 历史上数学家欧拉最先把关于 的多项式用记号 来表示,把 等于某数 时的多项式的值用 来表示.例如,对于多项式 ,当 时,多项式的值为 ,若 ,则 .18. “数形结合”思想在数轴上得到充分体现,如在数轴上表示数5和 的两点之间的距离,可列式表示为 ,或 ;表示数 和 的两点之间的距离可列式表示为 .已知 ,则 的最大值为.
17. 历史上数学家欧拉最先把关于 的多项式用记号 来表示,把 等于某数 时的多项式的值用 来表示.例如,对于多项式 ,当 时,多项式的值为 ,若 ,则 .18. “数形结合”思想在数轴上得到充分体现,如在数轴上表示数5和 的两点之间的距离,可列式表示为 ,或 ;表示数 和 的两点之间的距离可列式表示为 .已知 ,则 的最大值为.三、解答题
-
19. 计算:(1)、 ;(2)、 .20. 解方程(1)、 ;(2)、21. 化简求值: ,其中 , .22. 某公司去年1~3月平均每月亏损3.8万元,4~6月平均每月盈利3.6万元,7~10月平均每月盈利2.5万元,11~12月平均每月亏损3.5万元.(1)、如果把7~10月平均每月的盈利额记为 万元,那么,11~12月平均每月的盈利额可记为万元;(2)、请通过计算说明这个公司去年的盈亏情况;(3)、这个公司去年下半年平均每月盈利比上半年平均每月盈利多多少万元?23. 如图,已知线段 , ,射线 .点 , 为射线 上两点,且 , .
 (1)、请用尺规作图确定 , 两点的位置(要求:保留作图痕迹,不写作法);(2)、若 , ,求 的长.24. 某超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如下表:
(1)、请用尺规作图确定 , 两点的位置(要求:保留作图痕迹,不写作法);(2)、若 , ,求 的长.24. 某超市第一次用7000元购进甲、乙两种商品,其中甲商品的件数是乙商品件数的2倍,甲、乙两种商品的进价和售价如下表:甲
乙
进价(元/件)
40
60
售价(元/件)
50
80
(1)、该超市第一次购进的甲、乙两种商品各多少件?(2)、该超市第一次购进的甲、乙两种商品售完后,该超市第二次又以第一次的进价购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都售完以后获得的总利润比第一次获得的总利润少400元,求笫二次乙商品是按原价打几折销售?25. 如图是一个运算程序: (1)、若 , ,求 的值;(2)、若 ,输出结果 与 相同,求 的值.26. 定义:在同一平两内,有公共端点的三条射线中,一条射线是另两条射线组成夹角的角平分线,我们称这三条射线为“共生三线”.
(1)、若 , ,求 的值;(2)、若 ,输出结果 与 相同,求 的值.26. 定义:在同一平两内,有公共端点的三条射线中,一条射线是另两条射线组成夹角的角平分线,我们称这三条射线为“共生三线”.如图为一量角器的平面示意图, 为量角器的中心.作射线 , , ,并将其所对应的量角器外圈刻度分别记为 , , .
(1)、若射线 , , 为“共生三线”,且 为 的角平分线.①如图1, , ,则 ▲ ;
②当 , 时,请在图2中作出射线 , , ,并直接写出 的值;
③根据①②的经验,得 ▲ (用含 , 的代数式表示).
(2)、如图3, , .在 刻度线所在直线上方区域内,将 , , 按逆时针方向绕点 同时旋转,旋转速度分别为每秒 , , ,若旋转 秒后得到的射线 , , 为“共生三线”,求 的值.