河南省信阳市潢川县2020-2021学年七年级上学期数学期末考试试卷（A）

试卷更新日期：2021-05-13 类型：期末考试

进入出卷网下载

一、单选题

1. 在0.01，0，-5，- $\frac{1}{5}$ 这四个数中，最小的数是（）

A、 $0.01$ B、0 C、 $- 5$ D、 $- \frac{1}{5}$

查看试题解析
2. 下列说法正确的是 $($ $)$

A、一个数的绝对值一定比0大 B、绝对值等于它本身的数一定是正数 C、一个数的绝对值越大，表示它的点在数轴上越靠右 D、绝对值最小的数是0

查看试题解析
3. 有理数a，b在数轴上的位置如图所示，则下列结论正确的是（）

A、a>－2 B、a<－3 C、a<－b D、a>－b

查看试题解析
4. 下列运算正确的是（）

A、0﹣3＝﹣3 B、 $- \frac{5}{2} - \frac{1}{2} = - 2$ C、 $(- \frac{5}{2}) \div (- \frac{2}{5}) = 1$ D、（﹣2）×（﹣3）＝﹣6

查看试题解析
5. 下列各组中的两项，不是同类项的是 $($ $)$

A、3x与-5y B、0与 $- 7$ C、6xy与 $- \frac{1}{2} xy$ D、 $- 2 x^{2} y$ 与 $3 x^{2} y$

查看试题解析
6. 已知 $a + 2$ 的相反数是 $- 5$ ，则 $a$ 的值是（）

A、 $- 7$ B、3 C、 $- 3$ D、7

查看试题解析
7. 不透明袋子中装有一个几何体模型，两位同学摸该模型并描述它的特征，甲同学：它有4个面是三角形；乙同学：它有8条棱，该模型的形状对应的立体图形可能是（）

A、三棱柱 B、四棱柱 C、三棱锥 D、四棱锥

查看试题解析
8. 如图，∠1＝115°，∠AOB＝90°，点C，O，D在同一条直线上，则∠2的度数为（）

A、25° B、20° C、15° D、65°

查看试题解析
9. 甲看乙的方向为北偏东 $35 °$ ，那么乙看甲的方向是（）

A、南偏西 $35 °$ B、南偏东 $35 °$ C、南偏东 $55 °$ D、南偏西 $55 °$

查看试题解析
10. 小亮原计划骑车以10千米/时的速度由A地去B地，这样就可以在规定时间到达B地，但他因故比原计划晚出发15分钟，只好以15千米/时的速度前进，结果比规定时间早到6分钟，若设A，B两地间的距离为x千米，则根据题意列出的方程正确的为（）

A、 $\frac{x}{10} = \frac{x}{15}$ ＋15＋6 B、 $\frac{x}{10} = \frac{x}{15} + \frac{15}{60} + \frac{6}{60}$ C、 $\frac{x}{10} + \frac{15}{60} = \frac{x}{15} + \frac{6}{60}$ D、 $\frac{x}{10} + \frac{6}{60} = \frac{x}{15} + \frac{15}{60}$

查看试题解析

二、填空题

11. 下列各数： $\frac{1}{2}$ ，﹣（﹣3），﹣|﹣4|，0，﹣2² ， ﹣0.01，（﹣1）³ ，属于负数的有个.

查看试题解析
12. 如图，点O是直线AB上一点，∠AOC＝90°，将一个三角尺放在图中位置，使它的直角顶点与点O重合.若∠AOE＝ $117 ° 4 8^{'}$ ，则∠COD＝.

查看试题解析
13. 关于 $x$ 的方程 $\frac{2 x - m}{3} = 1$ 的解为2，则m的值是.

查看试题解析
14. 如图，长方形ABCD沿AE折叠，使D点落在BC边上的F点处，如果∠BAF=60°，则∠DAE等于度

查看试题解析
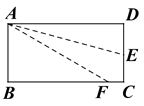15. 如图，将一个正三角形纸片剪成四个完全相同的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，……如此继续下去，剪的次数记为n，得到的正三角形的个数记为a_n ，则a₂₀₂₀＝.

查看试题解析

三、解答题

16. 计算：

(1)、（－4）×3－3÷（－ $\frac{1}{3}$ ）；

(2)、 $- 2^{2} - [(\frac{1}{3} - \frac{1}{2}) \times \frac{6}{11} - \frac{6}{11}]$ .

查看试题解析
17. 解方程：

(1)、2（x＋3）＝5x；

(2)、 $\frac{3 x + 2}{2} - 1 = \frac{2 x - 1}{4}$

查看试题解析
18. 先化简，再求值： $2 (a^{2} b - {ab}^{2}) - 3 (a^{2} b - 1) + 2 {ab}^{2} + 1$ ，其中 $a = 2$ ， $| b + 1 | = 0$ .

查看试题解析
19. 如图，数轴上的点A，B，C所对应的数分别为a，b，c，化简|2a|＋|b＋c|－|a－b－c|.

查看试题解析
20. 如图，已知O为直线AB上一点，射线OD和OE分别平分 $∠ A O C$ 和 $∠ B O C$ ，图中哪些角互为余角，请说明理由.

查看试题解析
21. 图1是边长为30cm的正方形纸板，裁掉阴影部分后将其折叠成如图2所示的长方体盒子，已知该长方体的宽是高的2倍.

(1)、设：长方体的高为xcm，则其宽为cm.

(2)、求长方体的体积.

查看试题解析
22. 某校球队计划购买12套队服和一批护具（护腕和扩膝），现从甲、乙两商场了解到：同一品牌的队服报价每套均为200元，护具报价每套均为50元.甲商场的优惠政策为：每购买一套队服赠送一套护具；乙商场的优惠政策为：所有队服和护具均按报价的八五折销售.若设该球队计划购买护具x套，则：

(1)、用含x的式子分别表示在甲、乙两商场购买队服和护具所需要的费用；

(2)、当购买多少套护具时，在甲、乙两商场购买队服和护具所需的费用相同？

(3)、如要购买30套护具，请设计出最省钱的购买方案.

查看试题解析
23. 如图，在数轴上点 $A$ 对应的数为 $- 20$ ，点 $B$ 对应的数为8，点 $D$ 对应的数为 $- 2$ ， $C$ 为原点.

(1)、 $B ， D$ 两点的距离是；

(2)、若点 $A$ 以每秒5个单位长度的速度沿数轴正方向运动，则2秒时 $A$ ， $D$ 两点的距离是；

(3)、若点 $A ， B$ 都以每秒4个单位长度的速度沿数轴正方向运动，而点 $C$ 不动， $t$ 秒时， $A ， B ， C$ 中有一点是三点所在线段的中点，求 $t$ 的值.

查看试题解析