福建省三明市永安市2020-2021学年七年级上学期数学期末考试试卷
试卷更新日期:2021-05-13 类型:期末考试
一、单选题
-
1. 如果收入10元记作 元,那么支出10元记作( )A、 元 B、 元 C、 元 D、 元2. 用一个平面去截下列几何体,截面不可能是圆的是 ( )A、
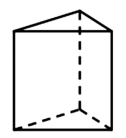 B、
B、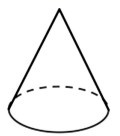 C、
C、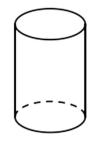 D、
D、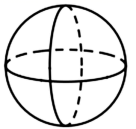 3. 如图,点A所表示的数的绝对值是( )
3. 如图,点A所表示的数的绝对值是( ) A、3 B、﹣3 C、 D、4. 港珠澳大桥是世界上最长的跨海大桥,被称为“新世界七大奇迹之一”,港珠澳大桥总长度55000米,则数据55000用科学记数法表示为( )A、 B、 C、 D、5. 下列判断正确的是( )A、 的次数是2 B、0不是单项式 C、 的系数是 D、 是四次三项式6. 如图所示,下列说法中正确的是( )
A、3 B、﹣3 C、 D、4. 港珠澳大桥是世界上最长的跨海大桥,被称为“新世界七大奇迹之一”,港珠澳大桥总长度55000米,则数据55000用科学记数法表示为( )A、 B、 C、 D、5. 下列判断正确的是( )A、 的次数是2 B、0不是单项式 C、 的系数是 D、 是四次三项式6. 如图所示,下列说法中正确的是( )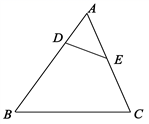 A、∠ADE就是∠D B、∠ABC可以用∠B表示 C、∠ABC和∠ACB是同一个角 D、∠BAC和∠DAE是不同的两个角7. 中学生骑电动车上学给交通安全带来隐患,为了解中学2 000名学生家长对“中学生骑电动车上学”的态度,从中随机调查400名家长,结果有360名家长持反对态度,则下列说法正确的是( )A、调查方式是普查 B、该校只有360名家长持反对态度 C、样本是360名家长 D、该校约有90%的家长持反对态度8. 等式就像平衡的天平,能与如图的事实具有相同性质的是( )
A、∠ADE就是∠D B、∠ABC可以用∠B表示 C、∠ABC和∠ACB是同一个角 D、∠BAC和∠DAE是不同的两个角7. 中学生骑电动车上学给交通安全带来隐患,为了解中学2 000名学生家长对“中学生骑电动车上学”的态度,从中随机调查400名家长,结果有360名家长持反对态度,则下列说法正确的是( )A、调查方式是普查 B、该校只有360名家长持反对态度 C、样本是360名家长 D、该校约有90%的家长持反对态度8. 等式就像平衡的天平,能与如图的事实具有相同性质的是( )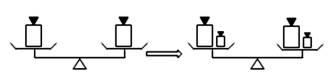 A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么9. 我国古代有很多经典的数学题,其中有一道题目是:良马日行二百里,驽马日行一百二十里,驽马先行十日,问良马几何追及之.意思是:跑得快的马每天走200里,跑得慢的马每天走120里,慢马先走10天,快马几天可追上慢马?若设快马 天可追上慢马,则由题意可列方程为( )A、 B、 C、 D、10. 按如图所示的程序计算,若开始输入的 的值为12,我们发现第一次得到的结果为6,第2次得到的结果为3,…,请你探索第2021次得到的结果为 ( )
A、如果 ,那么 B、如果 ,那么 C、如果 ,那么 D、如果 ,那么9. 我国古代有很多经典的数学题,其中有一道题目是:良马日行二百里,驽马日行一百二十里,驽马先行十日,问良马几何追及之.意思是:跑得快的马每天走200里,跑得慢的马每天走120里,慢马先走10天,快马几天可追上慢马?若设快马 天可追上慢马,则由题意可列方程为( )A、 B、 C、 D、10. 按如图所示的程序计算,若开始输入的 的值为12,我们发现第一次得到的结果为6,第2次得到的结果为3,…,请你探索第2021次得到的结果为 ( )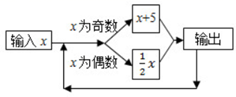 A、6 B、3 C、2 D、1
A、6 B、3 C、2 D、1二、填空题
-
11. 用“<”“>”或“=”号填空:- - .12. 时钟在 点整时,时针与分针的夹角为度.
 13. 如图为一个长方体,则该几何体从左面看得到的图形的面积为 .
13. 如图为一个长方体,则该几何体从左面看得到的图形的面积为 .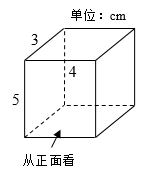 14. 幻方是相当古老的数学问题,我国古代的《洛书》中记载了最早的幻方---九宫图.将数字1~9分别填入如图所示的幻方中,要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15,则m的值为.
14. 幻方是相当古老的数学问题,我国古代的《洛书》中记载了最早的幻方---九宫图.将数字1~9分别填入如图所示的幻方中,要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15,则m的值为.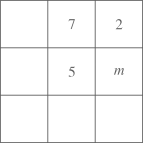 15. 已知代数式 的值为1,则代数式 的值为.16. 如图, 两点在数轴上表示的数分别为 ,且 和 满足 ,若一小球甲从点 处以1个单位/秒的速度向左运动,同时另一个小球乙从点 处以2个单位/秒的速度向左运动,甲乙两小球到原点的距离相等时,经历的时间是秒.
15. 已知代数式 的值为1,则代数式 的值为.16. 如图, 两点在数轴上表示的数分别为 ,且 和 满足 ,若一小球甲从点 处以1个单位/秒的速度向左运动,同时另一个小球乙从点 处以2个单位/秒的速度向左运动,甲乙两小球到原点的距离相等时,经历的时间是秒.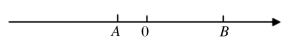
三、解答题
-
17.(1)、(2)、18.(1)、(2)、19.(1)、如图,用没有刻度直尺和圆规画图:
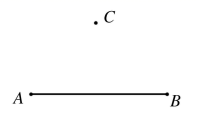
①点 是线段 处一点,画射线 ,画直线 ;
②延长线段 到 ,使 ;
(2)、在(1)的条件下,如果 , 是线段 的中点,求线段 的长.20. 解方程:(1)、4x﹣3(20﹣x)=3(2)、 221. 保护环境,让我们从垃圾分类做起.某区环保部门为了提高宣传实效,抽样调查了部分居民小区一段时间内生活垃圾(其中A、B、C、D分别表示可回收物、厨余垃圾、有害垃圾和其它垃圾)的分类情况,进行整理后,绘制了如下两幅尚不完整的统计图.试根据图表解答下列问题: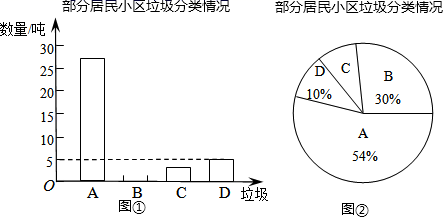 (1)、请将图①中的条形统计图补充完整;(2)、在图②中的扇形统计图中,“D”部分所对应的圆心角等于度;(3)、在抽样数据中,产生的有害垃圾共有多少吨?22. 小明练习跳绳,以1分钟跳165个为目标,并把5次1分钟跳绳的数量记录如下(超过165个的部分记为“+”,少于165个的部分记为“-”):-11,-6,-2,+4,+10(1)、小明在这5次跳绳练习中,1分钟最多跳多少个?(2)、小明在这5次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多几个?(3)、小明在这5次跳绳练习中,累计跳绳多少个?23. 小方家新买的房子要装修,住房户型呈长方形,平面图如下(单位:米).现准备铺设地面,三间卧室铺设木地板,其它区域铺设地砖.
(1)、请将图①中的条形统计图补充完整;(2)、在图②中的扇形统计图中,“D”部分所对应的圆心角等于度;(3)、在抽样数据中,产生的有害垃圾共有多少吨?22. 小明练习跳绳,以1分钟跳165个为目标,并把5次1分钟跳绳的数量记录如下(超过165个的部分记为“+”,少于165个的部分记为“-”):-11,-6,-2,+4,+10(1)、小明在这5次跳绳练习中,1分钟最多跳多少个?(2)、小明在这5次跳绳练习中,1分钟跳绳个数最多的一次比最少的一次多几个?(3)、小明在这5次跳绳练习中,累计跳绳多少个?23. 小方家新买的房子要装修,住房户型呈长方形,平面图如下(单位:米).现准备铺设地面,三间卧室铺设木地板,其它区域铺设地砖.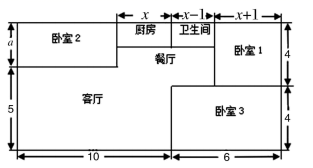 (1)、 ;(2)、铺设地面需要木地板和地砖各多少平方米(用含 的代数式表示)?(3)、按市场价格(含安装费),木地板单价为300元/平方米,地砖单价为100元/平方米.已知卧室2的面积为21平方米,则小方家铺设地面总费用是多少?24. 观察如图所示的图形,回答下列问题:
(1)、 ;(2)、铺设地面需要木地板和地砖各多少平方米(用含 的代数式表示)?(3)、按市场价格(含安装费),木地板单价为300元/平方米,地砖单价为100元/平方米.已知卧室2的面积为21平方米,则小方家铺设地面总费用是多少?24. 观察如图所示的图形,回答下列问题: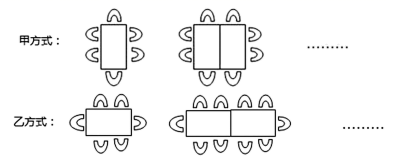 (1)、按甲方式将桌子拼在一起.
(1)、按甲方式将桌子拼在一起.4张桌子拼在一起共有个座位, 张桌子拼在一起共有个座位;
(2)、按乙方式将桌子拼在一起.5张桌子拼在一起共有个座位, 张桌子拼在一起共有个座位;
(3)、某食堂有 两个餐厅,现有90张这样的长方形桌子,计划把这些桌子全放在两个餐厅,每个餐厅都要放有桌子.将 张桌子放在 餐厅,按甲方式每3张拼成1张大桌子;将其余桌子都放在 餐厅,按乙方式每4张桌子拼成1张大桌子,若两个餐厅一共有370个座位,问 两个餐厅各有多少个座位?25. 已知直线 经过点 , , 是 的平分线.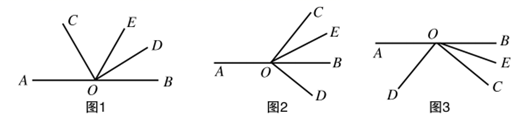 (1)、如图1,若 ,则 °, °;(2)、如图1,若 ,求 ;(用含 的式子表示)(3)、将图1中的 绕顶点 顺时针旋转到图2的位置,其它条件不变( , 是 的平分线, ),(2)中的结论是否还成立?试说明理由;(4)、将图1中的 绕顶点 逆时针旋转到图3的位置,其它条件不变,直接写出用含 的代数式表示 的式子.
(1)、如图1,若 ,则 °, °;(2)、如图1,若 ,求 ;(用含 的式子表示)(3)、将图1中的 绕顶点 顺时针旋转到图2的位置,其它条件不变( , 是 的平分线, ),(2)中的结论是否还成立?试说明理由;(4)、将图1中的 绕顶点 逆时针旋转到图3的位置,其它条件不变,直接写出用含 的代数式表示 的式子.