陕西省2021届高三下学期理数第三次教学质量检测试卷

试卷更新日期：2021-05-13 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知 $A = {x ∣ y = \log_{2} (3 x - 1)} ， B = {y ∣ x^{2} + y^{2} = 4}$ ，则 $A \cap B =$ （）

A、 $(0 ， \frac{1}{3})$ B、 $[- 2 ， \frac{1}{3})$ C、 $(\frac{1}{3} ， 2]$ D、 $(\frac{1}{3} ， 2)$

查看试题解析
2. 在复平面内，复数 $z = 2 - \frac{1 - i}{i}$ （ $i$ 为虚数单位）对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 《九章算术》中有如下问题：“今有勾五步，股一十二步，问勾中容圆，径几何？ ”其大意：“已知直角三角形两直角边长分别为5步和12步，问其内切圆的直径为多少步？”现若向此三角形内随机投一粒豆子，则豆子落在其内切圆外的概率是（）

A、 $\frac{2 π}{15}$ B、 $\frac{3 π}{20}$ C、 $1 - \frac{2 π}{15}$ D、 $1 - \frac{3 π}{20}$

查看试题解析
4. 已知双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1$ 的一条渐近线与直线 $2 x + y - 5 = 0$ 垂直，则双曲线C的离心率等于（）

A、 $\frac{\sqrt{5}}{2}$ B、 $\frac{\sqrt{10}}{3}$ C、 $\sqrt{10}$ D、 $2 \sqrt{2}$

查看试题解析
5. 某高中为了解学生课外知识的积累情况，随机抽取200名同学参加课外知识测试，测试共5道题，每答对一题得20分，答错得0分.已知每名同学至少能答对2道题，得分不少于60分记为及格，不少于80分记为优秀，测试成绩百分比分布图如图所示，则下列说法正确的是（）

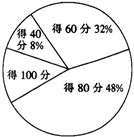A、该次课外知识测试及格率为90% B、该次课外知识测试得满分的同学有30名 C、该次测试成绩的中位数大于测试成绩的平均数 D、若该校共有3000名学生，则课外知识测试成绩能得优秀的同学大约有1440名

查看试题解析
6. 已知正项等比数列 ${a_{n}}$ 中，有 $a_{2} a_{10} = 25$ ，数列 ${b_{n}}$ 是等差数列，其前n项和为 $S_{n}$ ，且 $b_{5} = a_{6}$ ，则 $S_{9} =$ （）

A、15 B、30 C、45 D、90

查看试题解析
7. 下图是一个空间几何体的三视图，则该几何体的表面三角形中为直角三角形的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
8. 已知函数 $f (x) = 2 \cos (3 x + φ) + 3 (| φ | ⩽ \frac{π}{2})$ ，若 $\forall x \in (- \frac{π}{6}, \frac{π}{12})$ ， $f (x)$ 的图象恒在直线 $y = 3$ 的上方，则 $φ$ 的取值范围是（）

A、 $(\frac{π}{12}, \frac{π}{2})$ B、 $[\frac{π}{6}, \frac{π}{3}]$ C、 $(0, \frac{π}{4})$ D、 $(- \frac{π}{6}, \frac{π}{3})$

查看试题解析
9. 已知 $Δ O A B$ 是边长为1的正三角形，若点 $P$ 满足 $\overset{⇀}{O P} = (2 - t) \overset{⇀}{O A} + t \overset{⇀}{O B} (t \in R)$ ，则 $| \overset{⇀}{A P} |$ 的最小值为（）

A、 $\sqrt{3}$ B、1 C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{\sqrt{3}}{4}$

查看试题解析
10. 若 $2^{a} = 10, b = \log_{5} 10$ ，则 $\frac{1}{a} + \frac{1}{b} =$ （）

A、1 B、2 C、3 D、4

查看试题解析
11. 已知定义在R上的偶函数 $f (x)$ 在 $[0, + \infty)$ 上单调递增，记 $a = f ({0.3}^{2}), b = f (2^{0.3}), c = f (\log_{3} 2)$ ，则a ， b ， c的大小关系是（）

A、 $b < c < a$ B、 $c < a < b$ C、 $a < c < b$ D、 $b < a < c$

查看试题解析
12. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $A D = D D_{1} = 1 ， A B = \sqrt{3}$ ，E ， F ， G分别为 $A B ， B C ， C_{1} D_{1}$ 的中点，点P在平面 $A B C D$ 内，若直线 $D_{1} P / /$ 平面 $E F G$ ，则 $D_{1}$ 与满足题意的P构成的平面截正方体的截面面积为（）

A、 $\frac{2 \sqrt{2}}{3}$ B、 $\frac{\sqrt{6}}{2}$ C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{\sqrt{7}}{2}$

查看试题解析

二、填空题

13. 设x ， y满足约束条件 ${\begin{array}{l} x ⩾ 0 ， y ⩾ 0 \\ x - y ⩾ - 1 \\ x + y ⩽ 3 \end{array}$ ，则 $x - 9 y$ 的最小值是．

查看试题解析
14. $(x - 2 y) {(- x + y)}^{5}$ 展开式中，含 $x^{3} y^{3}$ 项的系数为．

查看试题解析
15. 已知抛物线 $C : y^{2} = 4 x$ ，过点 $(2, 0)$ 的直线 $l$ 交 $C$ 于 $A$ ， $B$ 两点，则直线 $O A, O B$ ( $O$ 为坐标原点)的斜率之积为.

查看试题解析
16. 已知数列 ${a_{n}}$ 与 ${b_{n}}$ 前n项和分别为 $S_{n}$ ， $T_{n}$ ，且 $a_{n} > 0, 2 S_{n} = a_{n}^{2} + a_{n}, n \in N^{*}$ ， $b_{n} = \frac{2^{n} + 1}{(2^{n} + a_{n}) (2^{n + 1} + a_{n + 1})}$ ，则 $T_{6} =$ ．

查看试题解析

三、解答题

17. 已知 $△ A B C$ 的三个内角A ， B ， C的对边分别为a ， b ， c ．若 $a (\sin A - \sin B) = c \sin C - b \sin B$ ．

(1)、求角C大小；

(2)、若 $△ A B C$ 的面积为 $2 \sqrt{3}, c = 2 \sqrt{3}$ ，求 $△ A B C$ 的周长．

查看试题解析
18. 如图所示，在多面体 $A B C D E F$ 中，四边形 $A D E F$ 为正方形， $A D / / B C$ ， $A D ⊥ A B$ ， $A D = 2 B C = 1$ ． $A B = \sqrt{3} ， B F = 2$ ．

(1)、证明：平面 $A D E F ⊥$ 平面 $A B C D$ ．

(2)、若三棱锥 $A - B D F$ 的外接球的球心为O ，求二面角 $A - C D - O$ 的余弦值．

查看试题解析

19. 大学先修课程，是在高中开设的具有大学水平的课程，旨在让学有余力的高中生早接受大学思维方式、学习方法的训练，为大学学习乃至未来的职业生涯做好准备.某高中成功开设大学先修课程已有两年，共有250人参与学习先修课程，这两年学习先修课程的学生都参加了高校的自主招生考试（满分100分），结果如下表所示：

分数 $a$	$95 \leq a \leq 100$	$85 \leq a < 95$	$75 \leq a < 85$	$60 \leq a < 75$	$a < 60$
人数	25	50	100	50	25
参加自主招生获得通过的概率	0.9	0.8	0.6	0.4	0.3

（Ⅰ）这两年学校共培养出优等生150人，根据下图等高条形图，填写相应列联表，并根据列联表检验能否在犯错的概率不超过0.01的前提下认为学习先修课程与优等生有关系？

	优等生	非优等生	总计
学习大学先修课程			250
没有学习大学先修课程
总计	150

（Ⅱ）已知今年全校有150名学生报名学习大学选项课程，并都参加了高校的自主招生考试，以前两年参加大学先修课程学习成绩的频率作为今年参加大学先修课程学习成绩的概率.

（ⅰ）在今年参与大学先修课程学习的学生中任取一人，求他获得高校自主招生通过的概率；

（ⅱ）某班有4名学生参加了大学先修课程的学习，设获得高校自主招生通过的人数为 $X$ ，求 $X$ 的分布列，试估计今年全校参加大学先修课程学习的学生获得高校自主招生通过的人数.

参考数据：

$P (K^{2} \geq k_{0})$	0.15	0.10	0.05	0.025	0.010	0.005
$k_{0}$	2.072	2.706	3.841	5.024	6.635	7.879

参考公式： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ ，其中 $n = a + b + c + d$

查看试题解析

20. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左、右焦点分别为 $F_{1} ， F_{2}$ ，椭圆E的离心率为 $\frac{\sqrt{3}}{2}$ ，且通径长为1．

(1)、求E的方程；

(2)、直线l与E交于M ， N两点（M ， N在x轴的同侧），当 $F_{1} M / / F_{2} N$ 时，求四边形 $F_{1} F_{2} N M$ 面积的最大值．

查看试题解析
21. 已知函数 $f (x) = 2 e^{x} - x^{2} - 2 (x - 1)$ （其中e为自然对数的底数）．

(1)、求 $f (x)$ 的单调区间；

(2)、若 $g (x) = f (x) + (a - 2) e^{x}$ 有两个极值点，求实数a的取值范围．

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，l的极坐标方程为 $ρ (\cos θ + 2 \sin θ) = 10$ ，C的参数方程为 ${\begin{array}{l} x = 3 \cos θ \\ y = 2 \sin θ \end{array}$ （ $θ$ 为参数， $θ \in R$ ）．

(1)、写出l的直角坐标方程和C的普通方程；

(2)、在C上取点M ，使点M到l的距离最小，并求出最小值．

查看试题解析
23. 设 $f (x) = | x - 1 | - | x + 3 |$ .

(1)、解不等式 $f (x) > 2$ ；

(2)、若不等式 $f (x) \leq k x + 1$ 在 $x \in [- 3 ， - 1]$ 上恒成立，求实数 $k$ 的取值范围．

查看试题解析