湘教版备考2021年中考数学三轮复习专题5一次函数

试卷更新日期：2021-05-12 类型：三轮冲刺

进入出卷网下载

一、单选题

1. 若数m是关于x的不等式组 ${\begin{array}{l} \frac{3 - 5 x}{2} \leq 9 - x \\ x < m \end{array}$ 至少有3个整数解且所有解都是 $2 x - 5 \leq 1$ 的解，且使关于x的分式 $\frac{4 x - 2}{x - 1} + \frac{3 m - 1}{1 - x} = 2$ 有整数解.则满足条件的所有整数m的个数是（）

A、5 B、4 C、3 D、2

查看试题解析
2. 若于 $x$ 的不等式组 ${\begin{array}{l} 3 x + 4 \leq 2 x + 8 \\ 1 - \frac{5 x + a}{2} < x \end{array}$ 有且仅有5个整数解，且关于 $y$ 的分式方程 $\frac{- y}{y - 1} - \frac{a - 3}{1 - y} = 1$ 有非负整数解，则满足条件的所有整数 $a$ 的和为（）

A、12 B、14 C、18 D、24

查看试题解析
3. 已知关于x的分式方程 $\frac{3 x - a}{x - 3}$ = $\frac{1}{3}$ 的解是非负数，那么a的取值范围是（）

A、a＞1 B、a≥1 C、a≥1且a≠9 D、a≤1

查看试题解析
4. 已知不等式4x-a≤0的正整数解是1，2，则a的取值范围是（）

A、8＜a＜12 B、8≤a＜12 C、8＜a≤12 D、8≤a≤12

查看试题解析
5. 已知函数 $y = 4 x^{2} - 4 x + m$ 的图像与x轴的交点坐标为 $(x_{1} ， 0)$ $(x_{2} ， 0)$ 且 $(x_{1} + x_{2}) (4 x_{1}^{2} - 5 x_{1} - x_{2}) = 8$ ，则该函数的最小值是（）

A、2 B、-2 C、10 D、-10

查看试题解析
6. 已知 $△ A B C$ 的三边长为a，b，c，且满足方程a²x²-（c²-a²-b²）x+b²=0，则方程根的情况是（）。

A、有两相等实根 B、有两相异实根 C、无实根 D、不能确定

查看试题解析
7. 若不等式 $2 | x - 1 | + 3 | x - 3 | \leq a$ 有解，则实数 $a$ 最小值是（）

A、1 B、2 C、4 D、6

查看试题解析
8. 设a、b是整数，方程x²+ax+b=0的一根是 $\sqrt{4 - 2 \sqrt{3}}$ ，则 $\frac{a^{2} + b^{2}}{a b}$ 的值为（）

A、2 B、0 C、-2 D、-1

查看试题解析
9. 若关于x的一元一次不等式组 ${\begin{array}{l} \frac{- 2 x + 3 m}{4} \leq 2 x \\ 2 x + 7 \leq 4 (x + 1) \end{array}$ 的解集为 $x \geq \frac{3}{2}$ ，且关于y的方程 $3 y - 2 = \frac{2 m - (5 - 3 y)}{2}$ 的解为非负整数，则符合条件的所有整数m的积为（）

A、2 B、7 C、11 D、10

查看试题解析
10. 若数m使关于x的不等式组 ${\begin{array}{l} \frac{3 + x}{2} - 1 \leq 3 \\ m - 2 x \leq - 2 \end{array}$ 有解且至多有3个整数解，且使关于y的分式方程 $\frac{3 y}{2 y - 4} = \frac{m - 2}{y - 2} + \frac{1}{2}$ 的解满足-3≤y≤4，则满足条件的所有整数m的个数是（　　）

A、6 B、5 C、4 D、3

查看试题解析
11. 已知整数k使得关于x、y的二元一次方程组 ${\begin{matrix} k x - y = 12 \\ 3 x - y = 3 \end{matrix}$ 的解为正整数，且关于x的不等式组 ${\begin{matrix} 3 x - k \geq 0 \\ \frac{1}{2} x - 2 < 1 \end{matrix}$ 有且仅有四个整数解，则所有满足条件的k的和为（）

A、4 B、9 C、10 D、12

查看试题解析
12. 若关于x的方程 $\frac{a}{x - 1} + 1 = \frac{x + a}{x + 1}$ 的解为负数，且关于x的不等式组 ${\begin{matrix} - \frac{1}{2} (x - a) > 0 \\ x - 1 \geq \frac{2 x + 1}{3} \end{matrix}$ 无解，则所有满足条件的整数a的值之和是（）

A、5 B、7 C、9 D、10

查看试题解析
13. 如果数m使关于x的不等式组 ${\begin{array}{l} \frac{1}{2} x < 2 \\ 6 x - m \geq 0 \end{array}$ 有且只有四个整数解，且关于x的分式方程 $\frac{x}{x - 1} - \frac{m}{1 - x} = 3$ 有整数解，那么符合条件的所有整数m的和是（）

A、8 B、9 C、﹣8 D、﹣9

查看试题解析
14. 从﹣3，﹣1， $\frac{1}{2}$ ，1，3这五个数中，随机抽取一个数，记为a，若数a使关于x的不等式组 ${\begin{matrix} \frac{1}{3} (2 x + 7) \geq 3 \\ x - a < 0 \end{matrix}$ 无解，且使关于x的分式方程 $\frac{x}{x - 3}$ ﹣ $\frac{a - 2}{3 - x}$ =﹣1有整数解，那么这5个数中所有满足条件的a的值之和是（）

A、﹣3 B、﹣2 C、﹣ $\frac{3}{2}$ D、 $\frac{1}{2}$

查看试题解析

二、填空题

15. 为刺激顾客到实体店消费，某商场决定在星期六开展促销活动.活动方案如下：在商场收银台旁放置一个不透明的箱子，箱子里有红、黄、绿三种颜色的球各一个（除颜色外大小、形状、质地等完全相同），顾客购买的商品达到一定金额可获得一次摸球机会，摸中红、黄、绿三种颜色的球可分别返还现金50元、30元、10元.商场分三个时段统计摸球次数和返现金额，汇总统计结果为：第二时段摸到红球次数为第一时段的3倍，摸到黄球次数为第一时段的2倍，摸到绿球次数为第一时段的4倍；第三时段摸到红球次数与第一时段相同，摸到黄球次数为第一时段的4倍，摸到绿球次数为第一时段的2倍，三个时段返现总金额为2510元，第三时段返现金额比第一时段多420元，则第二时段返现金额为元.

查看试题解析
16. 关于x的不等式组 $\{\begin{cases} x - a \leq 0 \\ 2 x + 3 a ＞ 0 \end{cases}$ 的解集中至少有5个整数解，则正数a的最小值是.

查看试题解析
17. 已知a>b>0，且 $\frac{2}{a} + \frac{1}{b} + \frac{3}{b-a} = 0$ ，则 $\frac{b}{a} =$ 。

查看试题解析
18. 已知正比例函数 $y = k x$ 的图像经过点 $A (- 2 ， 5)$ ，点 $M$ 在正比例函数 $y = k x$ 的图像上，点 $B (3 ， 0)$ ，且 $S_{△ A B M} = 10$ ，则点 $M$ 的坐标为．

查看试题解析
19. 如图，直线 $l ： y = \frac{\sqrt{3}}{3} x + 1$ 与 $x$ 轴正方向夹角为 $30 °$ ，点 $A_{1} ， A_{2} ， A_{3} ， \dots$ 在 $x$ 轴上，点 $B_{1} ， B_{2} ， B_{3} ， \dots$ 在直线 $l$ 上， $Δ O B_{1} A_{1} ， Δ A_{1} B_{2} A_{2} ， Δ A_{2} B_{3} A_{3} \dots$ 均为等边三角形，则 $A_{2020}$ 的横坐标为．

查看试题解析
20. 已知直线 $y = k_{1} x + b_{1}$ 与直线 $y = k_{2} x + b_{2}$ 的交点坐标为 $(2, - 3)$ ，则直线 $y = k_{1} x - b_{1}$ 与直线 $y = k_{2} x - b_{2}$ 的交点坐标为.

查看试题解析
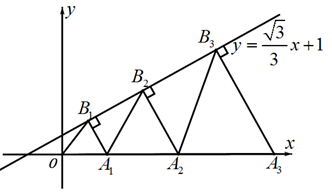21. 如图，将一块等腰直角三角板 ABC放置在平面直角坐标系中， ∠ACB = 90°，AC = BC，点 A在 y轴的正半轴上，点C在 x轴的负半轴上，点 B在第二象限， AC所在直线的函数表达式是 y = x + 2，若保持 AC的长不变，当点 A在 y轴的正半轴滑动，点 C随之在 x轴的负半轴上滑动，则在滑动过程中，点 B与原点 O的最大距离是.

查看试题解析
22. 已知一次函数 $y = (2 m - 1) x - 1 + 3 m (m$ 为常数），当x＜2时，y＞0，则 $m$ 的取值范围为．

查看试题解析
23. 如图， $A (1 ， 0)$ ， $B (3 ， 0)$ ， $M (4 ， 3)$ ，动点 $P$ 从点 $A$ 出发，以每秒 $1$ 个单位长的速度向右移动，且经过点 $P$ 的直线 $l ： y = - x + b$ 也随之移动，设移动时间为 $t$ 秒．若 $l$ 与线段 $B M$ 有公共点，则 $t$ 的取值范围为．

查看试题解析

三、解答题

24. 春节将至，八年级

(1)

班准备购买中性笔20支，练习本120本等学习文具作为新春联欢会奖品，决定由小明、小丽、小亮三人去小商品市场购买，甲、乙两文具店春节优惠大酬宾的方案如下：

甲店

中性笔4元 $/$ 支，练习本 $0.5$ 元 $/$ 本

买一送一

$($ 买一支中性笔送一本练习本 $)$

乙店

中性笔4元 $/$ 支，练习本 $0.5$ 元 $/$ 本

九折

$($ 按实际价款九折付款 $)$

3人看后，各自说出了自己的购买方案：小明选择甲店，小丽选择乙店，小亮选择先到甲店购买一部分，再到乙店购买一部分 $.$ 如果你也在场，对他们这三种方案有什么看法？哪种方案最省钱？

查看试题解析

25. 一次函数 $y = a x + b (b \neq 0)$ 与一次函数 $y = 2 - c x$ 的图象的交点的纵坐标为 $a + b$ ， $\frac{{(1 - a)}^{2}}{b c} + \frac{{(1 - b)}^{2}}{a c} + \frac{{(1 - c)}^{2}}{a b} = 3$ ．

(1)、求ab+bc+ca的值；

(2)、当 $a \neq 1, b \neq 1$ 时，求证： $\frac{b}{{(1 - a)}^{2}} = \frac{a}{{(1 - b)}^{2}}$ .

查看试题解析
26. 我市为创建“国家级森林城市”，政府决定对江边一处废弃荒地进行绿化，要求栽植甲、乙两种不同的树苗共6000棵，且甲种树苗不得多于乙种树苗．某承包商以26万元的报价中标承包了这项工程．根据调查及相关资料表明：移栽一棵树苗的平均费用为8元，甲、乙两种树苗的购买价及成活率如表：
品种
购买价（元/棵）
成活率
甲
20
90%
乙
32
95%
设购买甲种树苗x棵，承包商获得的利润为y元．请根据以上信息解答下列问题：

(1)、设y与x之间的函数关系式，并写出自变量x的取值范围；

(2)、承包商要获得不低于中标价16%的利润，应如何选购树苗？

(3)、政府与承包商的合同要求，栽植这批树苗的成活率必须不低于93%，否则承包商出资补栽；若成货率达到94%以上（含94%），则政府另给予工程款总额6%的奖励，该承包商应如何选购树苗才能获得最大利润？最大利润是多少？

查看试题解析
27. 如图，直线y= $\frac{1}{2}$ x+2交x轴于点A，交y轴于点B，点P（x，y）是线段AB上一动点（与A，B不重合），△PAO的面积为S，求S与x的函数关系式，并写出自变量的取值范围.

查看试题解析
28. 如图，在平面直角坐标系中，点F的坐标为（0，10）．点E的坐标为（20，0），直线l₁经过点F和点E，直线l₁与直线l₂、y= $\frac{3}{4}$ x相交于点P．

(1)、求直线l₁的表达式和点P的坐标；

(2)、矩形ABCD的边AB在y轴的正半轴上，点A与点F重合，点B在线段OF上，边AD平行于x 轴，且AB=6，AD=9，将矩形ABCD沿射线FE的方向平移，边AD始终与x 轴平行．已知矩形ABCD以每秒 $\sqrt{5}$ 个单位的速度匀速移动（点A移动到点E时止移动），设移动时间为t秒（t＞0）．
①矩形ABCD在移动过程中，B、C、D三点中有且只有一个顶点落在直线l₁或l₂上，请直接写出此时t的值；
②若矩形ABCD在移动的过程中，直线CD交直线l₁于点N，交直线l₂于点M．当△PMN的面积等于18时，请直接写出此时t的值．

查看试题解析
29. 如图①，平面直角坐标系中，O为原点，点A坐标为（﹣4，0），AB∥y轴，点C在y轴上，一次函数y= $\frac{1}{4}$ x+3的图象经过点B、C．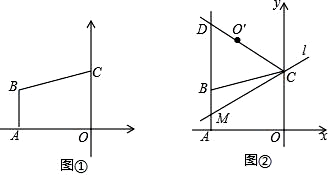

(1)、点C的坐标为，点B的坐标为；

(2)、如图②，直线l经过点C，且与直线AB交于点M，O'与O关于直线l对称，连接CO'并延长，交射线AB于点D．
①求证：△CMD是等腰三角形；
②当CD=5时，求直线l的函数表达式．

查看试题解析
30. 为倡导绿色出行，某共享单车近期登陆徐州，根据连续骑行时长分段计费：骑行时长在2h以内（含2h）的部分，每0.5h计费1元（不足0.5h按0.5h计算）；骑行时长超出2h的部分，每小时计费4元（不足1h按1h计算）．
根据此收费标准，解决下列问题：

(1)、连续骑行5h，应付费多少元？

(2)、若连续骑行xh（x＞2且x为整数）需付费y元，则y与x的函数表达式为；

(3)、若某人连续骑行后付费24元，求其连续骑行时长的范围．

查看试题解析
31. 如图所示，把矩形纸片OABC放入直角坐标系xOy中，使OA、OC分别落在x、y轴的正半轴上，连接AC，且AC=4 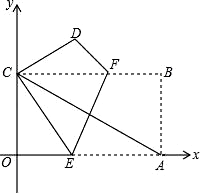$\sqrt{5}$ ， $\frac{O C}{O A} = \frac{1}{2}$

(1)、求AC所在直线的解析式；

(2)、将纸片OABC折叠，使点A与点C重合（折痕为EF），求折叠后纸片重叠部分的面积．

(3)、求EF所在的直线的函数解析式．

查看试题解析

四、综合题

32. 临近新年，某玩具店计划购进一种玩具，其进价为30元/个，已知售价不能低于成本价.在销售过程中，发现该玩具每天的销售量y（个）与售价x（元/个）之间满足一次函数关系，y与x的几组对应值如表：

x

40

45

50

55

y

80

70

60

50

(1)、求y与x之间的函数关系式；

(2)、如果规定该玩具每天的销售量不低于46件，当该玩具的售价定为多少元/个时，每天获取的利润w最大，最大利润是多少？

查看试题解析
33. 如图1，在平面直角坐标系中，直线 $A B ： y = k x + 6$ 分别与x轴、y轴交于A、B两点，其中 $A B = 3 \sqrt{5}$ ，点C在x轴的正半轴上，且 $O C = O B$ .

(1)、求直线AB的解析式；

(2)、将直线AB向下平移 $\frac{17}{2}$ 个单位长度得到直线 $l_{1}$ ，直线 $l_{1}$ 与y轴交于点E，与直线CB交于点D，过点E作y轴的垂线 $l_{2}$ ，若点P为y轴上一个动点，Q为直线 $l_{2}$ 上一个动点，求 $△ P Q D$ 的周长的最小值；

(3)、如图2，直线BC上有一点 $F (\frac{7}{2} ， y_{1})$ ，将直线BC绕点F顺时针旋转90°得到直线 $l_{3}$ ，与x轴交于点H，直线 $l_{3}$ 上有一点 $G (x_{1} ， - 4)$ ，点M是直线 $l_{1}$ 上一动点，是否存在点M使得 $△ M H G$ 为直角三角形，若存在，直接写出点 $M$ 的坐标；若不存在，说明理由.

查看试题解析
34. 如图，平面直角坐标系中，直线 $A B ： y = k x + 3 (k \neq 0)$ 交x轴于点 $A (4 ， 0)$ ，交y轴正半轴于点B，过点 $C (0 ， 2)$ 作y轴的垂线 $C D$ 交 $A B$ 于点E，点P从E出发，沿着射线 $E D$ 向右运动，设 $P E = n$ .

(1)、求直线 $A B$ 的表达式；

(2)、当 $△ A B P$ 为等腰三角形时，求n的值.

查看试题解析

35. 参照学习函数的过程与方法，探究函数

y = - \frac{2 | x - 2 |}{x} (x \neq 0)

的图象和性质，请按要求完成下列各小题.

(1)、请把下表补充完整，并在图中画出该函数图象；

…

$y = - \frac{2 | x - 2 |}{x}$

…

(2)、观察函数图象，下列关于函数性质的描述正确的是；

①函数 $y = - \frac{2 | x - 2 |}{x}$ 的图象关于原点中心对称；

②当 $x > 0$ 时，y随x的增大而减小；

③当 $x = 2$ 时，函数 $y = - \frac{2 | x - 2 |}{x}$ 取得最小值0；

④当 $x > 2$ 时，y随x的增大而减小；

(3)、请结合（1）问中画出的函数图象，直接写出关于x的不等式

y = - \frac{2 | x - 2 |}{x} + 2 x + 2 \leq 0

的解集（误差不超过0.2）.

查看试题解析

36. 在平面直角坐标系中，设一次函数 $y_{1} = k x + b$ ， $y_{2} = b x + k$ （k，b是实数，且 $b k \neq 0$ ）

(1)、若函数 $y_{1}$ 的图象过点 $(4, 3 b)$ ，求函数 $y_{1}$ 与x轴的交点坐标；

(2)、若函数 $y_{1}$ 的图象经过点 $(m, 0)$ ，求证：函数 $y_{2}$ 的图象经过点 $(\frac{1}{m}, 0)$ ；

(3)、若函数 $y_{1}$ 的图象不经过第一象限，且过点 $(2, - 3)$ ，当 $k < b$ 时，求k的取值范围.

查看试题解析
37. 为了“不忘历史，学习英雄”，学校开展“红色丰碑”演讲比赛；王老师负责为获奖同学购买奖品，现甲、乙两个商店正在做促销活动，分别给出了不同的优惠方案：
甲商店优惠方案：购买奖品金额超过300元后，超出300元的部分按8折收费；

乙商店优惠方案：购买奖品金额超过500元后，超出500元的部分按a折收费；

如果王老师到乙商店购买奖品，当奖品金额是600元时，实际需支付570元.

(1)、填空：a＝.

(2)、如果王老师到甲商店购买奖品金额x元，求实际支付y元与奖品金额x元之间的函数表达式.

(3)、如果王老师购买奖品的金额超过800元，那么到哪个商店进行采购更合算？

查看试题解析
38. 在平面直角坐标系中，点A的坐标为（4，0），直线l是经过点（0， $\frac{5}{2}$ ）且平行于x轴的直线，点B在直线l上，连接AB，设点B的横坐标为m（m＞0）.

(1)、如图1，当m＝9时，以AB为直角边作等腰直角三角形ABC，使∠BAC＝90°，求直线BC的函数表达式.

(2)、在图2中以AB为直角边作等腰直角三角形ABD，使∠ABD＝90°，连结OD，求△AOD的面积（用含m的代数式表示）.

(3)、在图3中以AB为直角边作等腰直角三角形ABP，当点P落在直线y＝ $\frac{5}{8}$ x+ $\frac{5}{2}$ 上时，求m的值.

查看试题解析
39. 表格中的两组对应值满足一次函数y＝kx＋b，函数图象为直线 $l_{1}$ ，如图所示.将函数y＝kx＋b中的k与b交换位置后得一次函数y＝bx＋k，其图象为直线 $l_{2}$ .设直线 $l_{1}$ 交y轴于点A，直线 $l_{1}$ 交直线 $l_{2}$ 于点B，直线 $l_{2}$ 交y轴于点C.

x

﹣2

4

y

﹣4

2

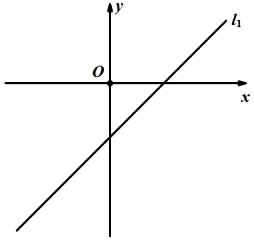(1)、求直线l₂的解析式；

(2)、若点P在直线 $l_{1}$ 上，且△BCP的面积是△ABC的面积的1＋ $\sqrt{2}$ 倍，求点P的坐标；

(3)、若直线y＝a分别与直线 $l_{1}$ ， $l_{2}$ 及y轴的三个交点中，其中一点是另两点所成线段的中点，求a的值.

查看试题解析
40. 请你用学习“一次函数”中积累的经验和方法研究函数 $y = - 2 | x | + 2$ 的图象和性质，并解决问题.

(1)、①当 $x = 0$ 时， $y = - 2 | x | + 2 = 2$
②当 $x > 0$ 时， $y = - 2 | x | + 2 =$ ；

③当 $x < 0$ 时， $y = - 2 | x | + 2 =$ ；

显然，②和③均为某个一次函数的一部分

(2)、在平面直角坐标系中，作出函数 $y = - 2 | x | + 2$ 的图象.

(3)、一次函数 $y = k x + b$ （ $k$ 为常数， $k \neq 0$ ）的图象过点 $(1 ， 3)$ ， ${\begin{array}{l} y = k x + b \\ y = - 2 | x | + 2 \end{array}$ 无解，结合函数的图象，直接写出 $k$ 的取值范围.

查看试题解析

品种	购买价（元/棵）	成活率
甲	20	90%
乙	32	95%

x	﹣2	4
y	﹣4	2